初中数学人教版九年级上册24.3 正多边形和圆完美版教学ppt课件

这是一份初中数学人教版九年级上册24.3 正多边形和圆完美版教学ppt课件，文件包含243正多边形与圆pptx、243正多边形与圆教学设计docx、243正多边形与圆导学案docx等3份课件配套教学资源，其中PPT共25页， 欢迎下载使用。
1 了解正多边形和圆的有关概念.2 理解并掌握正多边形半径和边长、边心距、中心角之间的关系.3 利用等分圆周的方法画出任意正多边形，会利用尺规作图的方法画特殊正多边形.
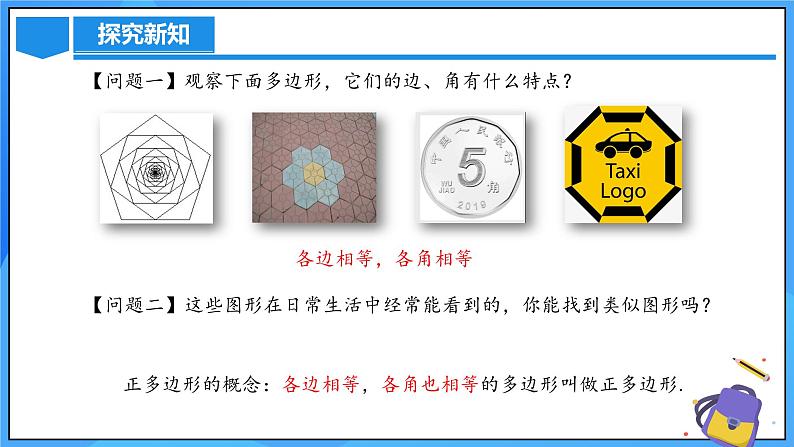
【问题一】观察下面多边形，它们的边、角有什么特点？
【问题二】这些图形在日常生活中经常能看到的，你能找到类似图形吗？
正多边形的概念：各边相等，各角也相等的多边形叫做正多边形.
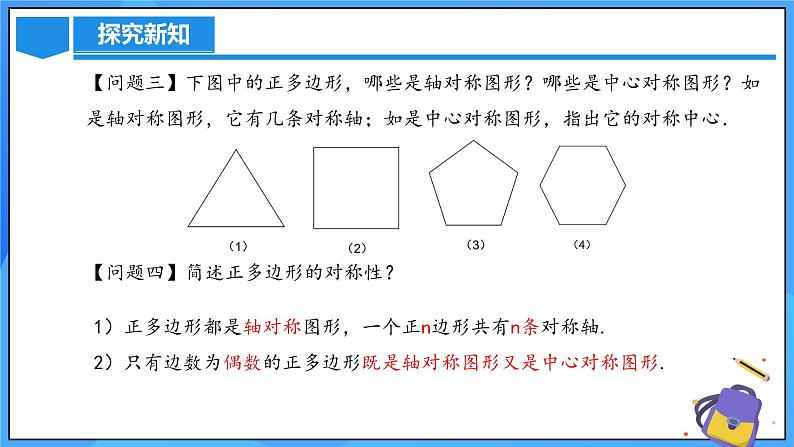
【问题三】下图中的正多边形，哪些是轴对称图形？哪些是中心对称图形？如是轴对称图形，它有几条对称轴；如是中心对称图形，指出它的对称中心．
【问题四】简述正多边形的对称性？
1）正多边形都是轴对称图形，一个正n边形共有n条对称轴.2）只有边数为偶数的正多边形既是轴对称图形又是中心对称图形.
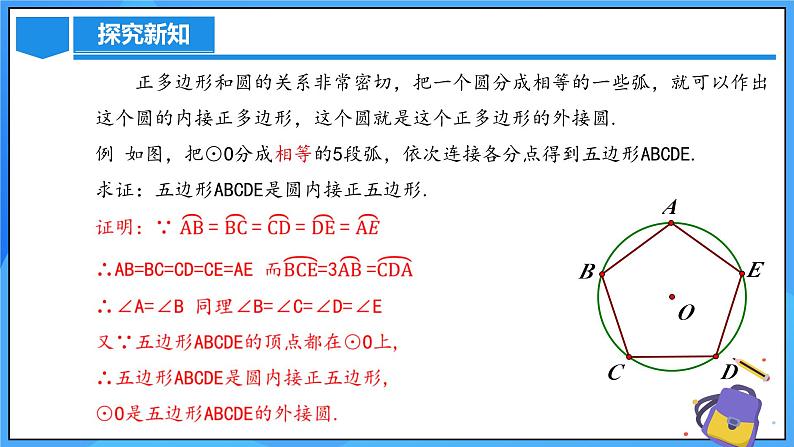
正多边形和圆的关系非常密切，把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多边形的外接圆.例 如图，把⊙O分成相等的5段弧，依次连接各分点得到五边形ABCDE. 求证：五边形ABCDE是圆内接正五边形.
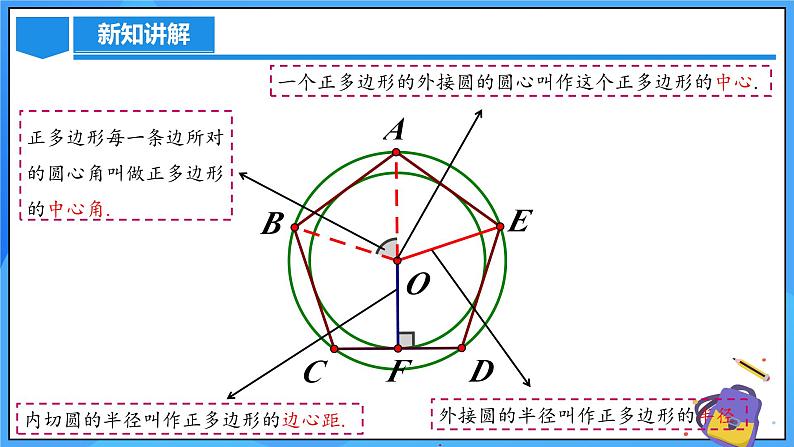
一个正多边形的外接圆的圆心叫作这个正多边形的中心.
外接圆的半径叫作正多边形的半径.
内切圆的半径叫作正多边形的边心距.
正多边形每一条边所对的圆心角叫做正多边形的中心角.
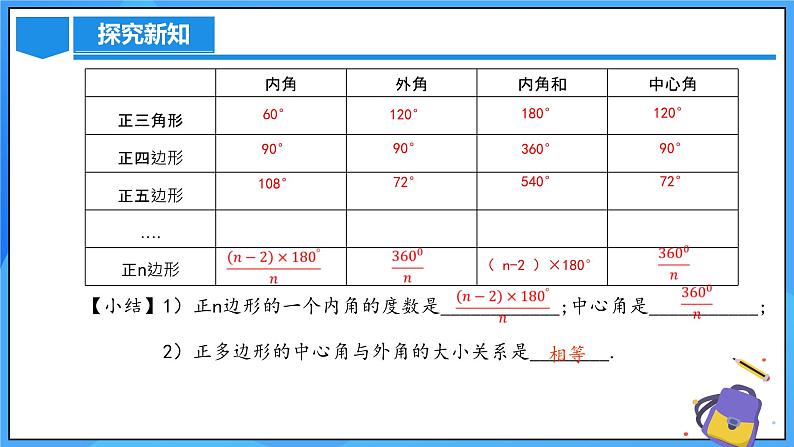
（ n-2 ）×180°
【小结】1）正n边形的一个内角的度数是____________;中心角是___________; 2）正多边形的中心角与外角的大小关系是________.
例1 有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积.
圆内接正多边形常见辅助线作法：
2）作边心距，构造直角三角形.
1）连半径，得中心角；
3）正多边形半径、边心距和正多边形边长已知其中两个量，第三个量可通过勾股定理求解.
4）若P为正n边形的周长，α为边长，r为边心距，正n边形的周长P为 _______,正n边形的面积为 _______,
1.正八边形的中心角为______.2.一个正多边形的一个外角为30°，则它的内角和为_____．3.若正六边形的边长为3，则其较长的一条对角线长为_____.4.如图，若干个全等的正五边形排成环状，图中所示的是前3个正五边形，要完成这一圆环还需正五边形的个数为_____________.
由于正多边形在生产、生活实际中有广泛的应用性，所以会画正多边形应是学生必备能力之一.【问题一】已知⊙O的半径为2cm，求作圆的内接正三角形.
作法：通过量角器度量使∠AOB=∠BOC=∠AOC=120°．
作法：通过量角器度量使∠BAO=∠CAO=30° ．
【问题二】如何把一个圆分成相等的一些弧，并画出这个圆的内接正多边形？
方法一：用量角器等分圆
【问题三】简述这两种方法的操作步骤及优缺点？
用尺规等分圆方法：先用尺规作图的方法等分圆，然后依次连接圆上各分点得到正多边形.【优缺点】这种方法有局限性，不是任意正多边形都能用此法作图，同时在作图时较复杂，同样存在作图的误差.
例2 尝试利用尺规画圆内接正四边形、正五边形、正八边形？
1.尝试画出圆内接正六边形？
作法：1）在⊙O中任意作一条直径AD．
2）分别以点A、D为圆心，⊙O的半径为半径作弧，与⊙O相交于点B、F和点C、E．
3）依次连接A、B、C、D、E、F各点．
正六边形ABCDEF就是所求作的圆内接正六边形．
1.通过本节课的学习,你学会了哪些知识？2.简述正多边形和圆的有关概念？3.简述正多边形半径和边长、边心距、中心角之间的关系？4. 简述画正多边形的方法？
P108：习题24.3 第1题，第4题，第5题，第6题