初中人教版24.4 弧长和扇形面积优质课教学ppt课件

这是一份初中人教版24.4 弧长和扇形面积优质课教学ppt课件，文件包含244弧长和扇形公式第一课时pptx、244弧长和扇形公式第一课时教学设计docx、244弧长和扇形公式第一课时导学案docx等3份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

1 理解弧长和扇形面积公式, 会计算弧长、扇形面积.2 灵活运用弧长及扇形面积公式解决实际问题.
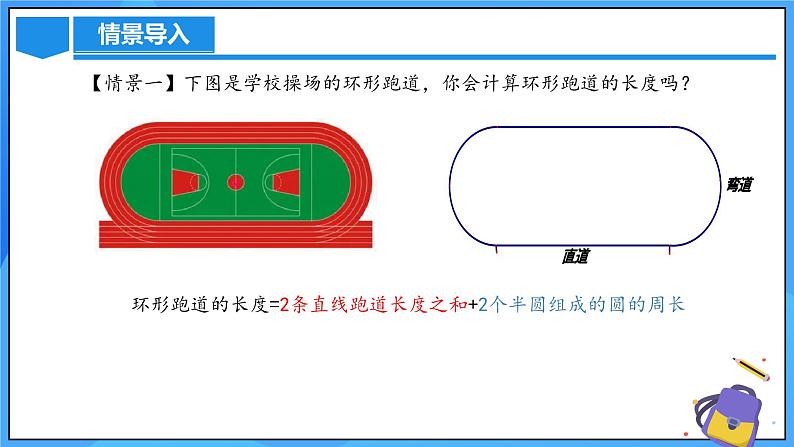
【情景一】下图是学校操场的环形跑道，你会计算环形跑道的长度吗？
环形跑道的长度=2条直线跑道长度之和+2个半圆组成的圆的周长
【情景二】运动会200米赛跑比赛中，为什么选手的起跑位置不在同一处？
因为不同的跑道，跑道一圈的长度不一样，要保证这些弯道的“展直长度”是一样的，所以运动员的起跑位置不在同一处，越靠近外侧的运动员所在跑道的长度越长，所以他的起跑位置越靠前.
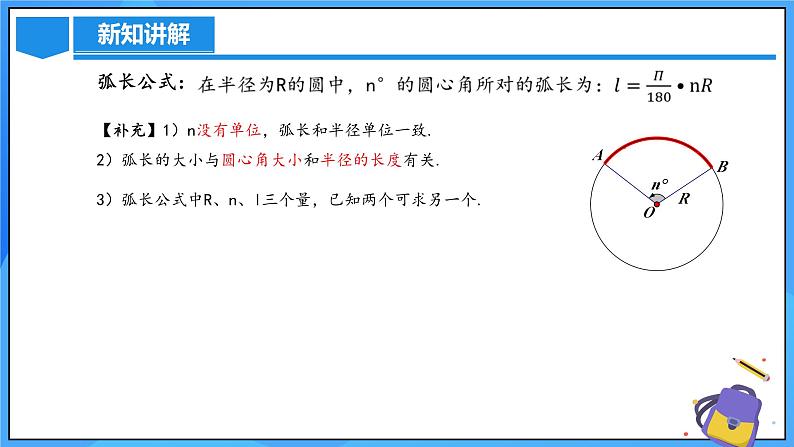
【问题一】我们知道，弧是圆的一部分，弧长就是圆周长的一部分.1) 求半径为R的圆的周长.2）圆的周长可以看作是多少度的圆心角所对的弧长.3） 1°的圆心角所对的弧长是：4） 45°的圆心角所对的弧长是：5) 90°的圆心角所对的弧长是：6) n°的圆心角所对的弧长是：
【补充】1）n没有单位，弧长和半径单位一致.2）弧长的大小与圆心角大小和半径的长度有关.3）弧长公式中R、n、l三个量，已知两个可求另一个.
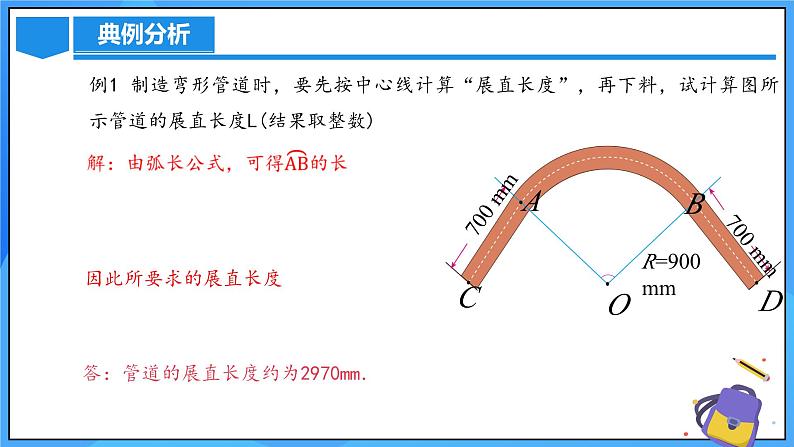
例1 制造弯形管道时，要先按中心线计算“展直长度”，再下料，试计算图所示管道的展直长度L(结果取整数)
答：管道的展直长度约为2970mm．
1.若扇形的圆心角为90°，半径为6 cm，则该扇形的弧长为__________ cm.2.若一弧长为10πcm，此弧所对的圆心角为120°，则该弧所在圆的半径为_________ cm．3.若一条弧的长为6πcm，弧的半径为6cm，则该弧所对的圆心角为__________ .
【问题二】观察图形，尝试给出扇形的概念？
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
【练一练】判断下列图片中哪些是扇形？
【问题三】由扇形的定义可知，扇形面积就是圆面积的一部分.1) 求半径为R的圆的面积.2）圆的面积可以看作是多少度的圆心角所对扇形的面积.3） 1°的圆心角所对扇形的面积是：4） 45°的圆心角所对扇形的面积是：5) 90°的圆心角所对扇形的面积是：6) n°的圆心角所对扇形的面积是：
【问题三】你觉得扇形的面积与哪些因素有关？
圆心角大小不变时，半径越长，面积越大.
圆的半径不变时，圆心角越大，面积越大.
例2 一个扇形的弧长为20πcm，半径为24cm，则该扇形的面积为_______.
1.扇形的圆心角为60°，半径为5 ,则这个扇形的弧长_______, 这个扇形的面积为______.2.已知扇形的圆心角为120°,弧长为20π，扇形面积为 ．3．一个扇形的弧长是20πcm，面积是240πcm2，则这个扇形的圆心角是_________
5. 如图，折扇完全打开后，OA、OB的夹角为120°，OA的长为30cm，AC的长为20cm，求图中阴影部分的面积S．
6.如图，水平放置的圆柱形排水管道的截面半径是0.6m，其中水面高0.3m，求截面上有水部分的面积？（结果保留小数点后两位）
1.通过本节课的学习,你学会了哪些知识？2.简述扇形的概念？3.简述弧长和扇形面积公式？
P113：练习第2题，第3题P115：习题24.4 第2题，第6题，第7题