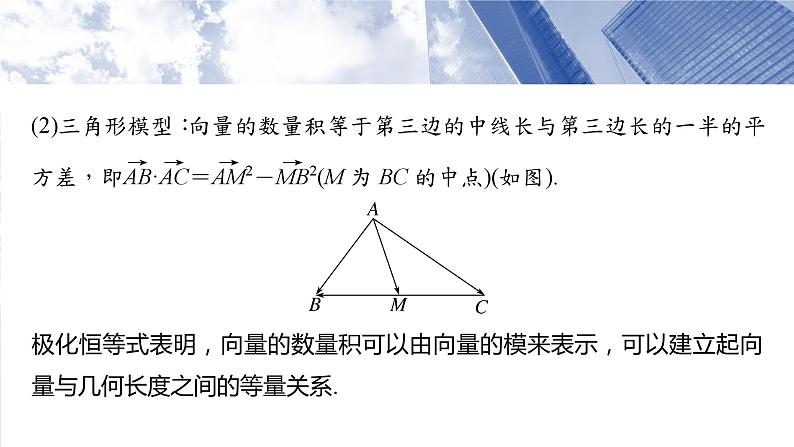
第五章　培优点7　极化恒等式 课件-2025高考数学一轮复习

这是一份第五章　培优点7　极化恒等式 课件-2025高考数学一轮复习，共46页。PPT课件主要包含了几何解释，方法三基向量法，∴由极化恒等式知，－610，方法一基底法，由极化恒等式得，取AB的中点E等内容，欢迎下载使用。

1.极化恒等式在平面向量中：(a＋b)2＝a2＋b2＋2a·b，(a－b)2＝a2＋b2－2a·b，
极化恒等式表明，向量的数量积可以由向量的模来表示，可以建立起向量与几何长度之间的等量关系.
题型一　利用极化恒等式求值
A.1 B.2 C.3 D.5
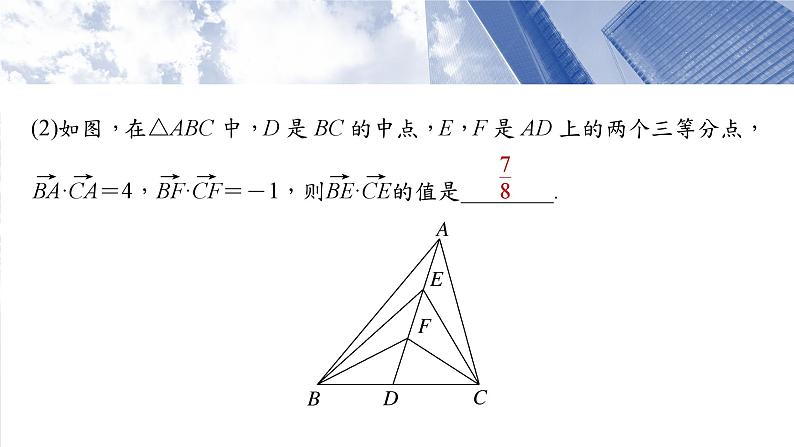
方法一(极化恒等式法)设BD＝DC＝m，AE＝EF＝FD＝n，则AD＝3n.由向量的极化恒等式，知
方法二(坐标法)以直线BC为x轴，过点D且垂直于BC的直线为y轴，建立如图所示的平面直角坐标系.设A(3a,3b)，B(－c,0)，C(c,0)，则E(2a,2b)，F(a，b)，
利用向量的极化恒等式可以快速对共起点(终点)的两向量的数量积问题进行转化，建立了向量的数量积与几何长度(数量)之间的桥梁，实现向量与几何、代数的巧妙结合，对于不共起点和不共终点的问题可通过平移等价转化为共起点(终点)的两向量的数量积问题，从而利用极化恒等式解决.
题型二　利用极化恒等式求最值(范围)
记线段PQ的中点为H(图略)，点O到直线AB的距离为d，
设MN的中点为A，连接OA，
方法二(极化恒等式法)
(1)利用极化恒等式求数量积的最值(范围)时，关键在于取第三边的中点，找到三角形的中线，再写出极化恒等式.(2)难点在于求中线长的最值(范围)，可通过观察图形或用点到直线的距离等求解.
如图所示，设P是线段AB上的任意一点，
由于P是线段AB上的任意一点，
如图所示，取BC的中点O，过点O作OH⊥BC交AD于点H，
如图，设BC的中点为D，AD的中点为M，连接DP，PM，
当且仅当M与P重合时取等号.
设圆C的半径为r，则r＝1，
(PM)min＝CM－r＝2－1＝1，
如图，圆C：(x－a)2＋(y＋a－1)2＝1的圆心C的坐标为(a,1－a)，则点C在直线l：x＋y－1＝0上，
因为点C是直线l：x＋y－1＝0上的动点，
5.已知a，b是平面内两个互相垂直的单位向量，若c满足(a－c)·(b－c)＝0，则|c|的最大值是
∵(a－c)·(b－c)＝0，∴(a＋b－2c)2＝(a－b)2，故c2＝(a＋b)·c，
在平行四边形ABOC中，因为OB＝OC，
设菱形ABOC对角线的交点为E，则由极化恒等式得