




- 重难点专题18 三角函数中w取值范围问题八大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用) 试卷 0 次下载
- 重难点专题19 三角函数零点与恒成立问题四大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用) 试卷 0 次下载
- 重难点专题21 三角函数压轴小题十五大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用) 试卷 0 次下载
- 重难点专题22 解三角形大题十四大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用) 试卷 0 次下载
- 重难点专题23 解三角形压轴小题十一大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用) 试卷 0 次下载
重难点专题20 三角函数解答题十一大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用)
展开一、注意基础知识的整合、巩固。进一步夯实基础,提高解题的准确性和速度。
二、查漏补缺,保强攻弱。在二轮复习中,针对“一模”考试中的问题要很好的解决,根据自己的实际情况作出合理的安排。
三、提高运算能力,规范解答过程。在高考中运算占很大比例,一定要重视运算技巧粗中有细,提高运算准确性和速度,同时,要规范解答过程及书写。
四、强化数学思维,构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结,以便于同学们在刷题时做到思路清晰,迅速准确。
五、解题快慢结合,改错反思。审题制定解题方案要慢,不要急于解题,要适当地选择好的方案,一旦方法选定,解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确,还要优化解题过程,提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
重难点专题20三角函数解答题十一大题型汇总
TOC \ "1-3" \h \z \u \l "_Tc146114079" 题型1识图问题 PAGEREF _Tc146114079 \h 1
\l "_Tc146114080" 题型2单调性问题 PAGEREF _Tc146114080 \h 4
\l "_Tc146114081" 题型3对称轴与对称中心问题 PAGEREF _Tc146114081 \h 5
\l "_Tc146114082" 题型4值域问题 PAGEREF _Tc146114082 \h 7
\l "_Tc146114083" 题型5最值问题 PAGEREF _Tc146114083 \h 9
\l "_Tc146114084" 题型6凑角求值问题 PAGEREF _Tc146114084 \h 11
\l "_Tc146114085" 题型7方程的根问题 PAGEREF _Tc146114085 \h 13
\l "_Tc146114086" 题型8零点问题 PAGEREF _Tc146114086 \h 14
\l "_Tc146114087" 题型9恒成立问题 PAGEREF _Tc146114087 \h 16
\l "_Tc146114088" 题型10有解问题 PAGEREF _Tc146114088 \h 17
\l "_Tc146114089" 题型11实际应用问题 PAGEREF _Tc146114089 \h 19
题型1识图问题
【例题1】(2022秋·安徽六安·高三六安二中校考阶段练习)已知函数fx=2sinωx+φ0<φ<π2的部分图像如图,该图像与y轴交于点A0,3,与x轴交于点B,C两点,D为图像的最高点,且△BCD的面积为π2.
(1)求fx的解析式及其单调递增区间;
(2)若将fx的图像向右平移π12个单位,再将所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数gx的图像,若gα=85π2<α<π,求sinα+5π12的值.
【变式1-1】1. (2022·全国·高三专题练习)已知函数fx=32sinωx+32csωx(ω>0)的周期为4.
(1)求fx的解析式;
(2)将fx的图像沿x轴向右平移23个单位得到函数gx的图像,P,Q分别为函数gx图像的最高点和最低点(如图),求∠OQP的大小.
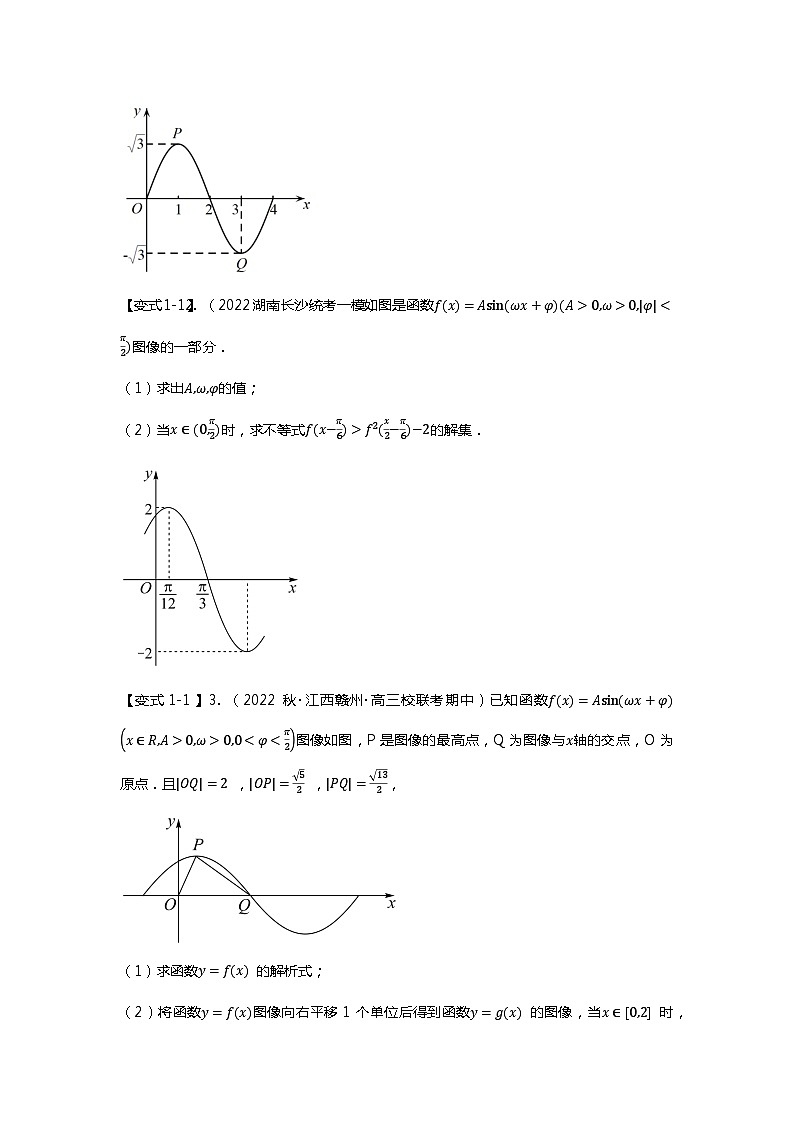
【变式1-1】2. (2022湖南长沙·统考一模)如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<π2)图像的一部分.
(1)求出A,ω,φ的值;
(2)当x∈(0,π2)时,求不等式f(x−π6)>f2(x2−π6)−2的解集.
【变式1-1】3. (2022秋·江西赣州·高三校联考期中)已知函数fx=Asinωx+φx∈R,A>0,ω>0,0<φ<π2图像如图,P是图像的最高点,Q为图像与x轴的交点,O为原点.且OQ=2 ,OP=52 ,PQ=132,
(1)求函数y=fx 的解析式;
(2)将函数y=fx图像向右平移1个单位后得到函数y=gx 的图像,当x∈0,2 时,求函数ℎx=fx·gx 的最大值.
【变式1-1】4. (2022秋·湖北武汉·高三华中师大一附中校考期中)函数fx=sinωx+φω>0,φ<π的部分图象如图所示,其中MN//x轴.
(1)求函数y=fx的解析式;
(2)将y=fx的图像向右平移π4个单位,再向上平移2个单位得到y=gx的图像,求gπ8的值.
题型2单调性问题
【例题2】(2023秋·湖南·高三校联考阶段练习)设函数fx=sinxsinx+π3−cs2x+14.
(1)求fx的最小正周期、最大值及取最大值时x的取值集合;
(2)讨论fx在区间−π2,π2上的单调性.
【变式2-1】1. (2023秋·山东临沂·高三统考期中)已知函数f(x)=3sinωxcsωx+cs2ωx﹣12(ω>0),与其图象的对称轴x=π6相邻的f(x)的个零点为5π12.
(1)判断函数f(x)在区间[﹣π6,π6]上的单调性;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,其中c=,f(C)=1.若向量π=(1,sinA),n=(sinB,﹣3),且π⊥n,求a,b.
【变式2-1】2. (2022·天津河西·统考三模)已知函数fx=cs2x+3sinxcsx−12x∈R
(1)求fx的最小正周期;
(2)讨论fx在区间−π4,π4上的单调性;
【变式2-1】3. (2022天津滨海新·校联考一模)设函数f(x)=(sinx+3csx)⋅cs(π2−x)tanx.
(1)求f(x)的最小正周期;
(2)讨论f(x)在区间(0,π2)上的单调性.
【变式2-1】4. (2022秋·四川雅安·高三雅安中学阶段练习)已知函数fx=23sinxcsx−2cs2x+1.
(1)求fx的最大值和对称中心坐标;
(2)讨论fx在0,π上的单调性.
【变式2-1】5.(2022春·安徽安庆·高三阶段练习)已知函数f(x)=sinx·(2csx−sinx)+cs2x.
(1)讨论函数f(x)在[0,π]上的单调性;
(2)设π4<α<π2,且f(α)=−5213,求sin2α的值.
题型3对称轴与对称中心问题
【例题3】(2021·陕西咸阳·校考二模)已知函数fx=2csxsinx−csx+1,x∈R
(1)求函数fx的对称轴和对称中心;
(2)当x∈π8,3π4,求函数fx的值域.
【变式3-1】1. (2022秋·天津静海·高三静海一中校考阶段练习)已知函数f(x)=2sinωxcsωx+3cs2ωx2+3cs2ωx−3+1.将周期为π的函数fx图像上所有点的横坐标伸长到原来的2倍,所得图像对应的函数为gx.
(1)求gx的单调区间;
(2)求gx图像的对称轴方程和对称中心坐标.
【变式3-1】2. (2022秋·江苏苏州·高三苏州市第五中学校开学考试)已知函数f(x)=5sinxcsx−53cs2x+532(x∈R).
(1)求f(x)的周期和最值;
(2)求f(x)的单调增区间;
(3)写出f(x)的图象的对称轴方程和对称中心坐标.
【变式3-1】3. (2022·山西吕梁·统考一模)已知函数f(x)=2asin2x+2sinxcsx−a的图象过点(0,−3).
(1)求常数a;
(2)求函数f(x)的最小正周期、单调区间、对称轴方程、对称中心坐标;
(3)当x∈[0,π2]时,求函数f(x)的值域.
【变式3-1】4. (2022秋·安徽阜阳·高三安徽省临泉第一中学校联考阶段练习)设函数fx=cs2x−π6−3cs2x−12.
(1)求fx的最小正周期及其图象的对称中心;
(2)若x0∈5π12,2π3且fx0=33−12,求cs2x0的值.
【变式3-1】5.(2021秋·安徽六安·高三六安市裕安区新安中学校考阶段练习)已知向量a=(sinωx+csωx,sinωx),向量b=(sinωx−csωx,23csωx),设函数fx=a⃑⋅b⃑+1x∈R的图象关于直线x=π3对称,其中常数ω∈(0,2).
(1)求函数fx的单调递减区间;
(2)将函数fx的图象向左平移π12个单位,再向下平移1个单位,得到函数gx的图象,求出函数gx对称中心.
题型4值域问题
【例题4】(2023春·陕西宝鸡·高三校考阶段练习)设函数fx=2sinπ6x+π3.
(1)列表并画出y=fx,x∈−2,10的图象;
(2)求函数gx=f1+x+f4−x在区间0,6上的值域.
【变式4-1】1. (2023秋·河南·高三郑州一中校联考阶段练习)设函数fx=sinx+2csx.
(1)是否存在m>0,使得fx=fm−x对∀x∈R恒成立?若存在,试给出一个符合题意的实数m并加以证明;若不存在,请说明理由;
(2)若x∈−π3,π时,求fx的值域.
【变式4-1】2. (2023·全国·高三专题练习)已知函数fx=sinxcsx−3cs2x+32.
(1)求函数fx的单调递减区间;
(2)将函数fx的图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,再将所得图象向左平移π6个单位,得到函数gx的图象,求函数ℎx=12fx+g2x在x∈π6,7π12的值域.
【变式4-1】3. (2023秋·河南·高三校联考阶段练习)在△ABC中,A+B=2C且csA+sinB=sinA+csB.
(1)求角B的大小;
(2)设函数fx=2csxsinx+π3−2sin2xsinB+3sinxcsxcs2A+C,当x∈π4,3π8时,求fx的值域.
【变式4-1】4. (2023春·陕西西安·高三西安中学校考阶段练习)已知函数fx=sinπ−ωxcsωx+cs2ωxω>0,y=fx的图象的一个对称中心到最近的对称轴的距离为π4.
(1)求ω的值;
(2)将函数y=fx的图象上各点的横坐标缩短到原来的12,纵坐标不变,得到函数y=gx的图象,求函数y=gx在区间0,π4上的值域.
【变式4-1】5.(2021秋·重庆涪陵·高三重庆市涪陵高级中学校校考阶段练习)已知数f(x)=3sinωx+π6+2sin2ωx2+π12−1(ω>0)的相邻两对称轴间的距离为π2.
(1)求f(x)的解析式;
(2)将函数f(x)的图像向右平移π6个单位长度,再把横坐标缩小为原来的12(纵坐标不变),得到函数y=g(x)的图像,当x∈−π12,π6时,求函数g(x)的值域.
(3)对于第(2)问中的函数g(x),记方程g(x)=43在x∈π6,4π3,上的根从小到依次为x1,x2,⋯xn,试确定n的值,并求x1+2x2+2x3+⋯+2xn−1+xn的值.
【变式4-5】6.(2022·全国·高三专题练习)设函数f(x)=sinx−csx (x∈R) .
(1)求函数y=f(x)⋅f(−x)的最小正周期及其对称中心;
(2)求函数y=[f(x)]2+fx+π42在−π4,π4上的值域.
题型5最值问题
【例题5】(2023·辽宁沈阳·东北育才双语学校校考一模)已知函数f(x)=2cs2ωx+23sinωxcsωx+a(ω>0,a∈R).再从条件①、条件②、条件③这三个条件中选择能确定函数f(x)解析式的两个合理条件作为已知,条件①:f(x)的最大值为1;条件②:f(x)的一条对称轴是直线x=−π12ω;条件③:f(x)的相邻两条对称轴之间的距离为π2.求:
(1)求函数f(x)的解析式;并求f(x)的单调递增区间、对称中心坐标;
(2)若将函数f(x)图象上的点纵坐标不变,横坐标变为原来的12,再向右平移π12单位,得到函数g(x)的图象,若g(x)在区间[0,m]上的最小值为g(0),求m的最大值.
【变式5-1】1. (2023秋·北京·高三北京市八一中学校考开学考试)已知函数fx=2sinωx+φ+1ω>0,φ<π2,fx图象上两相邻对称轴之间的距离为π2; ;
(Ⅰ)在①fx的一条对称轴x=−π3;②fx的一个对称中心5π12,1;③fx的图象经过点5π6,0这三个条件中任选一个补充在上面空白横线中,然后确定函数的解析式;
(Ⅱ)若动直线x=t t∈0,π与fx和gx=23sinxcsx的图象分别交于P、Q两点,求线段PQ长度的最大值及此时t的值.
注:如果选择多个条件分别解答,按第一个解答计分.
【变式5-1】2. (2022秋·安徽·高三校联考期末)设向量m=(2csωx,3sinωx),n=(csωx,2csωx),函数f(x)=m⋅n+a(ω>0,a∈R)的最大值为1,且图象相邻两个对称中心之间的距离为π2.
(1)求函数f(x)的解析式;
(2)若将函数f(x)图象上所有点的纵坐标不变,横坐标变为原来的12,再向右平移π12个单位长度,得到函数g(x)的图象,若g(x)在区间[0,t]上的最小值为g(0),求实数t的最大值.
【变式5-1】3. (2022秋·宁夏银川·高三校考阶段练习)在△ABC中,角A,B,C的对边分别为a,b,c,且sinCcsB2=(233−csC)sinB2.
(1)当B=π3,求sinC+sinA的值
(2)求B的最大值.
【变式5-1】4. (2020秋·上海黄浦·高三上海市大同中学校考阶段练习)已知a=(3,−1),b=sin2x,cs2x−π3,函数f(x)=a⋅b.
(1)若A={x|f(x)=0,x∈R},B=[−π,π],用列举法表示A∩B;
(2)求函数f(x)的单调递增区间以及当函数取得最大值时,a和b的夹角θ.
【变式5-1】5. (2020·安徽马鞍山·校联考一模)在△ABC中的内角A、B、C,sin(A−B)=sinC−sinB,D是边BC的三等分点(靠近点B),t=sin∠ABDsin∠BAD.
(1)求A的大小.
(2)当t取最大值时,求tan∠ACD的值.
题型6凑角求值问题
【例题6】(2020秋·新疆·高三乌鲁木齐市第70中校考阶段练习)已知函数f(x)=3sinωx2csωx2+cs2ωx2+3csωx+π6−12(ω>0)的图象的两相邻对称轴间的距离为π2.
(1)求函数y=fx的解析式:
(2)已知角α,β,θ满足:fα2⋅fβ2=−423且α+β=3π4,tanθ=2,求sin(θ+α)sin(θ+β)cs2θ的值.
【变式6-1】1. (2022秋·山东枣庄·高三阶段练习)已知函数f(x)=2sinωxcsωx﹣23sin2ωx+3(ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为π2.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调增区间;
(Ⅲ)若f(α)=23,求sin(56π﹣4α)的值.
【变式6-1】2. (2021秋·河南·高三阶段练习)已知函数f(x)=2sin(ωx+ϕ)ω>0,ϕ<π2图象的一条对称轴方程为x=π6,这条对称轴与相邻对称中心之间的距离为π4.
(1)求f(x)的解析式;
(2)若sin4α−cs4α=−35,α∈0,π2,求fα+π3.
【变式6-1】3. (2022·全国·高三专题练习)已知函数f(x)=sinωx(sinωx+csωx)−12(ω>0)图象的相邻两条对称轴之间的距离为2π.
(1)求f(x)的单调递增区间以及f(x)图象的对称中心坐标;
(2)是否存在锐角α,β,使α+2β=2π3,f(α+π2)⋅f(2β+3π2)=38同时成立?若存在,求出角α,β的值;若不存在,请说明理由.
【变式6-1】4. (2022·全国·高三专题练习)在下列三个条件中任选一个,补充在下面问题中,并加以解答.①图象上一个最低点为M2π3,−2;②直线x=π6是其图象的一条对称轴;③点N11π12,0是其图象的一个对称中心.
问题:已知函数fx=4csωxsinωx+φ−1 ω>0,0<φ<π2的图象与x轴的交点中,相邻两个交点之间的距离为π2,且______.
(1)求fx的解析式;
(2)若α为锐角,且fα2=65,求fα+π12的值.
【变式6-1】5.(2022·浙江·高三专题练习)已知函数f(x)=2sin(ωx+φ) 0<ω<6,|φ|<π2,f(x)的图象的一条对称轴是x=π3,一个对称中心是7π12,0.
(1)求f(x)的解析式;
(2)已知△ABC是锐角三角形,向量m =fB2+π12,fπ4,n =fB2+π3,fB+π3,且m⊥n,sinC=35,求csA.
【变式6-1】6.(2022秋·宁夏银川·高三校考阶段练习)已知函数fx=3csx⋅csx−π2+sin2x−π6−12.
(1)求fx的对称中心;
(2)若x∈0 , π4,fx=36,求cs2x的值.
【变式6-1】7.(2022·全国·高三专题练习)在①函数fx=12sin2ωx+π2+sin2ωx−π6;②函数fx=csωxsinωx+π6−14ω>0这两个条件中任选一个,补充在下面问题中,并解答.
已知________,函数fx的图像相邻两对称中心之间的距离为π2.
(1)求函数fx的最小正周期和单调递增区间;
(2)若0<θ<π6,且fθ=310,求cs2θ的值.
题型7方程的根问题
【例题7】(2023·辽宁大连·育明高中校考一模)已知函数fx=2sinωxcsφ+2sinφ−4sin2ωx2sinφ ω>0,φ<π,其图像的一条对称轴与相邻对称中心的横坐标相差π4,______,从以下两个条件中任选一个补充在空白横线中.
①函数fx的图像向左平移π3个单位长度后得到的图像关于y轴对称且f0<0;
②函数fx的图像的一个对称中心为π12,0且fπ6>0.
(1)求函数fx的解析式;
(2)若关于x的方程fx+12f2x−π3=2m有实根,求实数m的取值范围.
【变式7-1】1. (2023秋·辽宁沈阳·高三沈阳二十中校考开学考试)已知函数f(x)=3sin(ωx+φ)+2sin2ωx+φ2−1(ω>0,0<φ<π)为奇函数,且fx图象的相邻两对称轴间的距离为π2.
(1)求fx的解析式与单调递减区间;
(2)已知fx在−π6,5π6时,求方程2f2x+3fx−3=0的所有根的和.
【变式7-1】2. (2022·全国·高三专题练习)已知函数f(x)=3sinωx+φ+2sin2ωx+φ2−1(ω>0,0<φ<π)为奇函数,且f(x)图象的相邻两对称轴间的距离为π2.
(1)求f(x)的解析式与单调递减区间;
(2)将函数f(x)的图象向右平移π6个单位长度,再把横坐标缩小为原来的12(纵坐标不变),得到函数y=gx的图象,当x∈0,π2时,求方程2g2(x)+3gx−3=0的所有根的和.
【变式7-1】3. (2023·全国·高三专题练习)已知函数f(x)=sinx⋅csx+π6.
(1)求函数f(x)的最小正周期和对称中心;
(2)若x∈0,5π6,方程f(x)−m=0有两个实数解,求实数m的取值范围.
【变式7-1】4. (2022·全国·高三专题练习)已知∠A是△ABC的内角,函数fx=csx−3π2sinx−A的最大值为14.
(1)求∠A的大小;
(2)若gx=2fx+14,关于x的方程4gx2−mgx+1=0在x∈−π3,π3内有两个不同的解,求实数m的取值范围.
题型8零点问题
【例题8】(2022·全国·高三专题练习)已知函数f(x)=22sinx+π4csx−1.
(1)当x∈−π8,π8时,求f(x)的值域;
(2)是否同时存在实数a和正整数n,使得函数g(x)=f(x)−a在x∈0,nπ上恰有2021个零点?若存在,请求出所有符合条件的a和n的值;若不存在,请说明理由.
【变式8-1】1. (2023·山西太原·太原五中校考一模)已知函数fx=sinωx+φ(ω>0,0<φ<π)的周期为π,图象的一个对称中心为π4,0,将函数fx图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移π2个单位长度后得到函数gx的图象.
(1)求函数fx与gx的解析式;
(2)求实数a与正整数n,使得Fx=fx+agx在0,nπ内恰有2023个零点.
【变式8-1】2. (2022秋·福建福州·高三校考阶段练习)由两角和差公式我们得到倍角公式cs2θ=2cs2θ−1,实际上cs3θ也可以表示为csθ的三次多项式.
(1)试用csθ表示cs3θ;
(2)求sin18∘的值;
(3)已知方程4x3−3x−12=0在(−1,1)上有三个根,记为x1,x2,x3,求证:4x13+4x23+4x33=32.
【变式8-1】3. (2023·全国·高三专题练习)已知函数fx=22sin3xcs3x+22cs23x−2.
(1)求fx的单调递增区间;
(2)若函数gx=fx−2在n,m上恰有2023个零点,求m−n的最大值.
【变式8-1】4. (2020秋·安徽六安·高三校考阶段练习)将函数f(x)=−cs4x的图象向右平移π4个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数记作gx.
(1)在△ABC中,三个内角A,B,C且A
【变式8-1】5. (2022秋·安徽六安·高三六安一中阶段练习)已知函数fx=3sin2x+2cs2x+m0≤x≤π2.
(1)若函数fx的最大值为6,求常数m的值;
(2)若函数fx有两个零点x1和x2 ,求m的取值范围,并求x1和x2的和;
(3)在(1)的条件下,若gx=t−1fx−3sinx−3csx3csx+sinxt≥2,讨论函数gx的零点个数.
题型9恒成立问题
【例题9】(2023春·北京·高三校考阶段练习)已知函数fx=3sin2ωx−cs2ωx(0<ω<2),再从条件①、条件②、条件③中选择一个作为已知,
(1)求fx的解析式;
(2)当x∈0,π2时,关于x的不等式fx≤m恒成立,求实数m的取值范围.
条件①:函数fx的图象经过点π3,2;
条件②:函数fx的图象可由函数gx=2sin2x的图象平移得到;
条件③:函数fx的图象相邻的两个对称中心之间的距离为π2.
注:如果选择条件①、条件②和条件③分别解答,按第一个解答计分.
【变式9-1】1. (2020·全国·校联考二模)已知函数y=f(x)的定义域为(0,+∞),且满足f(xy)=f(x)+f(y),当x∈(1,+∞)时,有f(x)>0,且f(2)=1.
(1)求不等式f(4t)−f(1−t)<2的解集;
(2)对任意x∈0,π2,f2sin2x+π4−22csx−π4−5a+2⩾f(6−2a)恒成立,求实数a的取值范围.
【变式9-1】2. (2022秋·广东东莞·高三校考阶段练习)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π2)部分图象如下图所示.
(1)求函数f(x)的解析式,并写出f(x)单调递增区间;
(2)函数g(x)=4f(x)−a⋅2f(x)+3(a∈R),若对任意x∈[π4,π2],都有g(x)≥0恒成立,求实数a取值范围.
【变式9-1】3. (2022秋·江苏南通·高三江苏省如皋中学统考阶段练习)已知a=sinωx,csωx,b=csωx,3csωx,fx=a⋅b−32aω>0.函数y=fx的最小正周期为π
(1)求函数fx在0,π内的单调递增区间;
(2)若关于x的不等式fx−π6>2msinx+π4−2csx−π4在0,π2内恒成立,求实数m的取值范围.
【变式9-1】4. (2020秋·江苏无锡·高三校考阶段练习)已知π=sinx,csx,n=csx,−csx,设fx=π⋅n.
(1)当x∈0,π2时,求fx的值域;
(2)若锐角△ABC满足fC=0,且不等式tan2A+tan2B+mtanAtanB+1≥0恒成立,求m的取值范围.
【变式9-1】5.(2020秋·海南·高三海南华侨中学校考阶段练习)已知函数fx=xcsx,gx=sinx,x∈0,π2.
(1)求证:fx≤gx;
(2)若ax
【例题10】(2022·全国·高三专题练习)已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π2)的图象与x轴的交于A,B两点,A,B两点的最小距离为π2,且该函数的图象上的一个最高点的坐标为π12,2.
(1)求函数fx的解析式;
(2)求证:存在大于π3的正实数x0,使得不等式|f(x)|lnx>23在区间x0,e有解.(其中e为自然对数的底数)
【变式10-1】1. (2021秋·北京·高三北京一七一中校考期中)已知的函数f(x)=csx(23sinx+csx)−sin2x.
(1)求函数fx的最小正周期和单调递增区间;
(2)若当x∈0,π2时,关于x的不等式f(x)≥m有解,求实数m的取值范围.
【变式10-1】2. (2023秋·辽宁·高三辽河油田第二高级中学校考期末)已知函数fx=csx23sinx+csx−sin2x.
(Ⅰ)求函数fx的单调递增区间和最小正周期;
(Ⅱ)若当x∈0,π2时,关于x的不等式fx≥m______,求实数m的取值范围.
请选择①和②中的一个条件,补全问题(Ⅱ),并求解.其中,①有解;②恒成立.
【变式10-1】3. (2020秋·安徽合肥·高三合肥市第六中学校考期中)已知函数fx=csx.
(1)已知α,β为锐角,fα+β=−55,tanα=43,求cs2α及tanβ−α的值;
(2)函数gx=3f2x+1,若关于x的不等式g2x≥a+1gx+3a+3有解,求实数a的最大值.
【变式10-1】4. (2022·全国·高三专题练习)已知函数fx=2sinxcsx−23sin2x+3,gx=sinx.
(Ⅰ)若x∈0,π3,求函数fx的值域;
(Ⅱ)将函数fx图象向右平移π6个单位,再将图象上每一点的横坐标不变,纵坐标变为原来的2倍得到函数ℎx的图象,并设Fx=ℎx+tgx+gx+π2.若Fx>0在0,π2上有解,求实数t的取值范围.
【变式10-1】5.(2022秋·山东济南·高三山东省实验中学校考阶段练习)已知函数f(x)=sin(2x+π6)+2(sin2x−1).
(1)求函数y=f(x)的单调减区间和对称轴;
(2)若不等式f(x)+1
【例题11】(2023·全国·高三专题练习)如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0, ω>0,x∈[0,8])的图像,且图像的最高点为S(6,43).赛道的后一段为折线段MNP,为保证参赛队员的安全,限定∠MNP=120°.
(1)求实数A和ω的值以及M、P两点之间的距离;
(2)试求折线段MNP的最大值.
【变式11-1】1. (2022·山东济南·高三山东省实验中学校考阶段练习)某街道路宽OD为103米,在道路的边缘点O安装高度为11米(即OA=11)的路灯,灯杆AB与灯柱OA成120°角.当灯罩轴线BC与灯杆AB垂直时,灯罩轴线正好通过OD的中点.
(1)求灯杆AB的长;
(2)路灯采用可旋转灯口方向的锥形灯罩,灯罩轴线BC与灯的边缘光线(如图BM,BN)都成30°角.设∠ABC=θ,是否存在θ,能使路灯的光线照亮整个路面?若存在,求tanθ的取值范围;若不存在,在M,N都落在路面OD上的条件下,求MN的最大值.
【变式11-1】2. (2022·山东济南·高三山东省实验中学校考阶段练习)某街道路宽OD为103米,在道路的边缘点O安装高度为11米(即OA=11)的路灯,灯杆AB与灯柱OA成120°角.当灯罩轴线BC与灯杆AB垂直时,灯罩轴线正好通过OD的中点.
(1)求灯杆AB的长;
(2)路灯采用可旋转灯口方向的锥形灯罩,灯罩轴线BC与灯的边缘光线(如图BM,BN)都成30°角.设∠ABC=θ,是否存在θ,能使路灯的光线照亮整个路面?若存在,求tanθ的取值范围;若不存在,在M,N都落在路面OD上的条件下,求MN的最大值.
【变式11-1】3. (2022·全国·高三专题练习)如图,某圆形小区有两块空余绿化扇形草地AOB(圆心角为π3)和COD(圆心角为π2),BD为圆的直径.现分别要设计出两块社区活动区域,其中一块为矩形区域OEFG,一块为平行四边形区域MNPQ,已知圆的直径PF=2百米,且点P在劣弧AB上(不含端点),点Q在OA上、点G在OC上、点M和N在OB上、点E在OD上,记∠BOP=θ.
(1)经设计,当OE−12MN达到最大值时,取得最佳观赏效果,求θ取何值时,OE−12MN最大,最大值是多少?
(2)设矩形OEFG和平行四边形MNPQ面积和为S,求S的最大值及此时cs2θ的值.
【变式11-1】4. (2022春·上海浦东新·高三上海市实验学校校考阶段练习)如图,在矩形ABCD中,AB=2,AD=3,点E为AB的中点,F,G分别为线段AD,BC上的点,且EF⊥EG,∠AEF=θ.
(1)若△EFG的周长为f(θ),求f(θ)的解析式及θ的取值范围;
(2)求f(θ)的最值.
【变式11-1】5.(2022·全国·高三专题练习)如图,直线l1∥l2,点A是l1,l2之间的一个定点,过点A的直线EF垂直于直线l1,AE=m,AF=n(m,n为常数),点B,C分别为l1,l2上的动点,已知∠BAC=π3.设∠ACF=α(0<α<π3),△ABC的面积为Sα.
(1)若α=π4,求梯形EFCB的面积;
(2)写出Sα的解析式;
(3)求Sα的最小值.
1. (2023·湖南常德·常德市一中校考模拟预测)如图有一块半径为4,圆心角为π2的扇形铁皮AOB,P是圆弧AB上一点(不包括A,B),点M,N分别半径OA,OB上.
(1)若四边形PMON为矩形,求其面积最大值;
(2)若△PBN和△PMA均为直角三角形,求它们面积之和的取值范围.
2. (2023·北京东城·统考模拟预测)已知函数fx=23sinωxcsωx−2sin2ωx+10<ω<2.在下面两个条件中选择其中一个,完成下面两个问题:
条件①:在fx图象上相邻的两个对称中心的距离为π2;
条件②:fx的一条对称轴为x=π6.
(1)求ω;
(2)将fx的图象向右平移π3个单位(纵坐标不变),得到函数gx的图象,求函数gx在−π3,π3上的值域.
3. (2023·广东深圳·红岭中学校考模拟预测)已知函数f(x)=cs4x−sin4x+sin2x−π6.
(1)求函数f(x)在0,π2上的单调递增区间;
(2)将函数f(x)的图象向左平移φ0<φ<π4个单位长度后得到函数g(x)的图象,若函数g(x)的图象关于点π3,0成中心对称,在−π4,α上的值域为−12,1,求α的取值范围.
4. (2022·四川泸州·统考一模)已知函数fx=sinωx+φω>0,0<φ<π的图象相邻两最高点的距离为π,且有一个对称中心为π3,0.
(1)求ω和φ的值;
(2)若fθ−π6=223,且π8<θ<π4,求fθ的值.
5. (2022·四川成都·统考一模)设函数y=f(x)满足:对任意的实数x∈R有f(sinx)=−cs2x+cs2x+2sinx−3.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若方程f(x)=2a|x−12|有解,求实数a的取值范围.
6. (2020·浙江·统考模拟预测)已知△ABC中,函数f(x)=cs(3π2+x)⋅sin(A−x)的最大值为14.
(1)求∠A的大小;
(2)若g(x)=2(f(x)+14),方程4[g(x)]2−m[g(x)]+1=0在x∈[−π3,π3]内有两个不同的解,求实数m取值范围.
7. (2020·浙江·模拟预测)已知函数fx=4x2+2x.
(1)若存在实数a,b,x,使得fasinx+bcsx=−14,求a2+b2的最小值;
(2)证明:存在实数c,当fcsx=c时,恒有fcs4x=c.
8. (2023·北京·统考高考真题)设函数f(x)=sinωxcsφ+csωxsinφω>0,|φ|<π2.
(1)若f(0)=−32,求φ的值.
(2)已知f(x)在区间−π3,2π3上单调递增,f2π3=1,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使函数f(x)存在,求ω,φ的值.
条件①:fπ3=2;
条件②:f−π3=−1;
条件③:f(x)在区间−π2,−π3上单调递减.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
9. (2021·浙江·统考高考真题)设函数fx=sinx+csx(x∈R).
(1)求函数y=fx+π22的最小正周期;
(2)求函数y=f(x)fx−π4在0,π2上的最大值.
10. (2020·山东·统考高考真题)小明同学用“五点法”作某个正弦型函数y=Asin(ωx+φ)A>0,ω>0,φ<π2在一个周期内的图象时,列表如下:
根据表中数据,求:
(1)实数A,ω,φ的值;
(2)该函数在区间3π4,5π4上的最大值和最小值.
注意正余弦"第一零点"和"第二零点"的区别和联系.
正弦“第一零点”:x=2kπ;正弦“第二零点”:x=π+2kπ.
余弦"第一零点":x=-π2+2kx;余弦"第二零点":x=π2+2kπ2.
函数
Y=sinx
Y=csx
Y=tanx
单调性
[−π2+2kπ,π2+2kπ](kϵZ)上递增;
[π2+2kπ,3π2+2kπ](kϵZ)上递减
[−π+2kπ,2kπ](kϵZ)上递增;
[2kπ,π+2kπ](kϵZ)上递减
(−π2+kπ,π2+kπ)(kϵZ)上递增
函数y=Asin(ωx+φ)(A>0,ω>0)的性质
(1)奇偶性:φ=kπ(k∈Z)时,函数y=Asin(ωx+φ)为奇函数;
φ=kπ+π2(k∈Z)时,函数y=Asin(ωx+φ)为偶函数.
(2)周期性:y=Asin(ωx+φ)存在周期性,其最小正周期为T=2πω.
(3)单调性:根据y=sin t和t=ωx+φ(ω>0)的单调性来研究,由-π2+2kπ≤ωx+φ≤π2+2kπ(k∈Z)得单调增区间;由π2+2kπ≤ωx+φ≤3π2+2kπ(k∈Z)得单调减区间.
(4)对称性:利用y=sin x的对称中心为(kπ,0)(k∈Z)来解,令ωx+φ=kπ(k∈Z),求得其对称中心.
利用y=sin x的对称轴为x=kπ+π2(k∈Z)来解,令ωx+φ=kπ+π2(k∈Z)得其对称轴
求三角函数值域的常用方法
(1)求解形如y=asin x+b(或y=acs x+b)的函数的最值或值域问题时,利用正、余弦函数的有界性(-1≤sin x≤1,-1≤cs x≤1)求解.求三角函数取最值时相应自变量x的集合时,要注意考虑三角函数的周期性.
(2)求解形如y=asin2x+bsin x+c(或y=acs2x+bcs x+c),x∈D的函数的值域或最值时,通过换元,令t=sin x(或cs x),将原函数转化为关于t的二次函数,利用配方法求值域或最值即可.求解过程中要注意t=sin x(或cs x)的有界性.
1.“打散”:角度不一致,可以拆开
2.“重组”:系数次幂一致,合并为正弦余弦,便于使用辅助角“化一”
1.可以直接求解:五点画图法思维2,可以换元求解
x
−π6
π12
π3
7π12
5π6
ωx+φ
0
π2
π
3π2
2π
Asin(ωx+φ)
0
3
0
-3
0
重难点专题18 三角函数中w取值范围问题八大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用): 这是一份重难点专题18 三角函数中w取值范围问题八大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用),文件包含重难点专题18三角函数中w取值范围问题八大题型汇总原卷版docx、重难点专题18三角函数中w取值范围问题八大题型汇总解析版docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。
重难点专题16 三角函数的图像与性质八大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用): 这是一份重难点专题16 三角函数的图像与性质八大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用),文件包含重难点专题16三角函数的图像与性质八大题型汇总原卷版docx、重难点专题16三角函数的图像与性质八大题型汇总解析版docx等2份试卷配套教学资源,其中试卷共79页, 欢迎下载使用。
重难点专题14 导数压轴小题十四大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用): 这是一份重难点专题14 导数压轴小题十四大题型汇总-【划重点】备战2024年高考数学重难点题型突破(新高考通用),文件包含重难点专题14导数压轴小题十四大题型汇总原卷版docx、重难点专题14导数压轴小题十四大题型汇总解析版docx等2份试卷配套教学资源,其中试卷共135页, 欢迎下载使用。












