2025年高考数学一轮复习-第六板块-函数与导数-微专题(二)函数的方程及实际应用【课件】

这是一份2025年高考数学一轮复习-第六板块-函数与导数-微专题(二)函数的方程及实际应用【课件】，共32页。PPT课件主要包含了关键点拨，答案D等内容，欢迎下载使用。
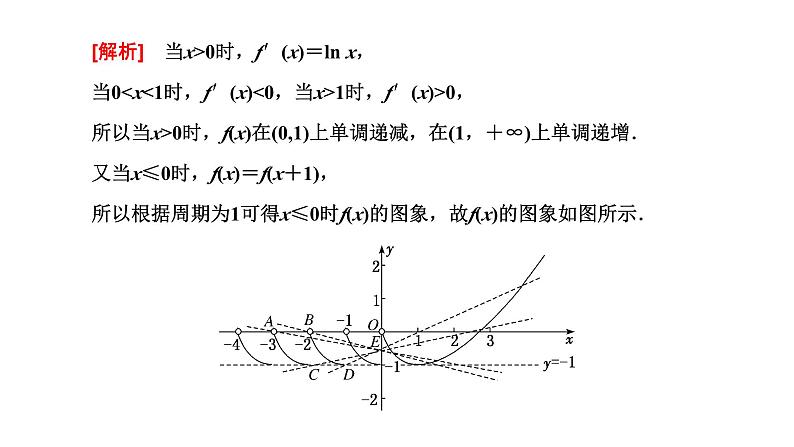
[解析]　当x>0时，f′(x)＝ln x，当00时，f(x)在(0,1)上单调递减，在(1，＋∞)上单调递增．又当x≤0时，f(x)＝f(x＋1)，所以根据周期为1可得x≤0时f(x)的图象，故f(x)的图象如图所示．
[例2]　(2022·赣州二模)已知定义在R上的函数y＝f(x)，对任意x都满足f(x＋2)＝f(x)，且当－1≤x≤1时，f(x)＝2x2，则函数g(x)＝f(x)－ln|x|的零点个数为(　　)A．12 B．14C．15 D．16[关键点拨]
[解析]　∵f(x＋2)＝f(x)，∴函数y＝f(x)是周期为2的周期函数．令g(x)＝f(x)－ln|x|＝0，则f(x)＝ln|x|，由题意得函数g(x)＝f(x)－ln|x|的零点个数即为函数y＝f(x)的图象与函数y＝ln|x|的图象交点的个数．当－1≤x≤1时，f(x)＝2x2，在同一坐标系内画出函数y＝f(x)和函数y＝ln|x|的图象(如图所示)，结合图象可得两函数的图象有14个交点，∴函数g(x)＝f(x)－ln|x|的零点个数为14.[答案]　B
已知函数有零点求参数范围常用的方法
1．(2022·吕梁一模)已知函数f(x)＝|3－2x－x2|的图象和直线2x＋ay＋7＝0有三个交点，则a＝______.
解析：不妨设x1