2025年高考数学一轮复习-第六板块-函数与导数-微专题(五)大题专攻——“函数与导数”大题的规范解题路径【课件】

这是一份2025年高考数学一轮复习-第六板块-函数与导数-微专题(五)大题专攻——“函数与导数”大题的规范解题路径【课件】，共28页。
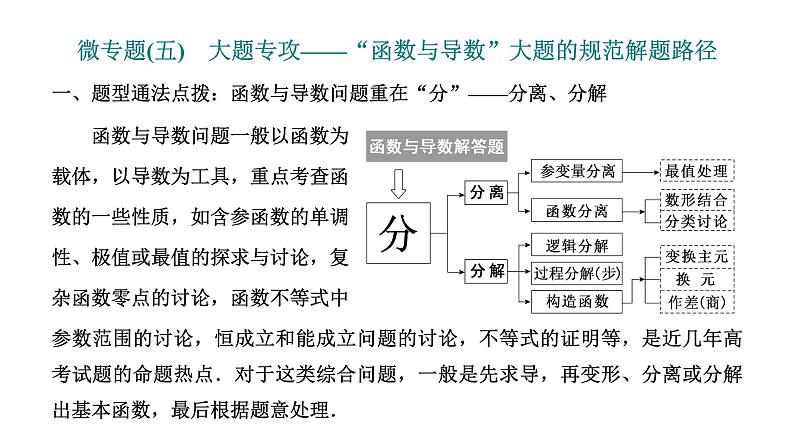
二、高频考法精研：有关x与ex，ln x的组合函数的解题技法　有关x与ex，ln x的组合函数是高考的常考内容，常将基本初等函数的概念、图象与性质糅合在一起，发挥导数的工具作用，应用导数研究函数性质、证明相关不等式(或比较大小)、求参数的取值范围(或最值)等．熟悉与x，ex，ln x有关的函数图象特征，在解答相关问题时做到“有形可寻”，对解题大有帮助.
[例1]　已知函数f(x)＝ex－ax2，若a＝1，证明：当x≥0时，f(x)≥1.
技法三　借助ln x≤x－1或ex≥x＋1进行放缩[例3]　已知函数f(x)＝xex－aln x(e为自然对数的底数，e＝2.718…)．(1)若f(x)在(0,1)上单调递减，求实数a的取值范围；(2)当a＝－1时，设g(x)＝x[f(x)－xex]－x3＋x2－b，若函数g(x)存在零点，求实数b的最大值．
设h(x)＝(x2＋x)ex，x∈(0,1)，则h′(x)＝ex(x2＋3x＋1)，当x∈(0,1)时，x2＋3x＋1>0，则h′(x)>0，所以h(x)在(0,1)上单调递增，所以h(x)