初中人教版（2024）5.2 解一元一次方程图文ppt课件

这是一份初中人教版（2024）5.2 解一元一次方程图文ppt课件，共23页。PPT课件主要包含了复习巩固，讲授新课，化归思想，归纳总结，拓展提高等内容，欢迎下载使用。
1. 能够根据题意找出实际问题中的相等关系，列出一元一次方程； 2. 运用合并同类项解形如 ．
学习重点：列方程，用合并同类项解一元一次方程．独立分析实际问题中的相等关系，列方程；体会方程中的化归思想．
学习难点：独立分析实际问题中的相等关系，列方程．
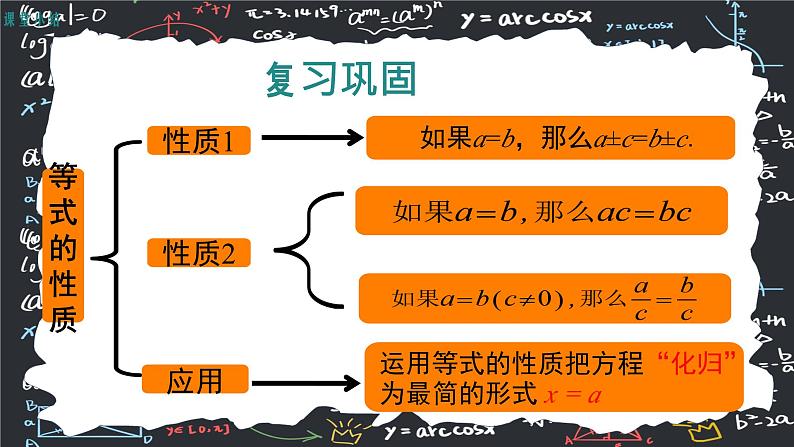
　 1、应用等式的性质解下列方程并检验: (1) x+3= 6； (2) 0.2x=4 (3) -2x+4=0； (4)
我们已经知道，直接利用等式的性质可以解简单的方程.本节我们将结合方程的具体特点，继续研究如何解一元一次方程
例1、某校三年共购买计算机140台，去年购买数量是前年的2倍，今年购买的数量又是去年的2倍．前年这个学校购买了多少台计算机？
设前年这个学校购买了计算机x台，尝试列出方程.
　　设前年这个学校购买了计算机x台，则去年购买计算机_____台，今年购买计算机_____台，
根据“三年共购买计算机 140台”，可以得到如下相等关系 前年购买量十去年购买量十今年购买量=140.
x+2x+4x＝140
问题2：解方程的最终目标形式是什么？
他们是同类项，可以合并成一项
合作探究（小组讨论）问题1：观察方程的左边有什么特点？
解方程，就是把方程变形，化归为 x = a(a为常数) 的形式.
问题3：怎样解这个方程呢？
思考：如何将此方程转化为x＝a（a为常数）的形式?
依据：乘法分配律的逆用
思考1：合并同类项的依据是什么？
思考2：系数化为1的依据是什么？
思考3：上述解方程中合并同类项和系数化为1的作用分别是什么？蕴含了什么数学思想？
还有不同的设法吗？还可以列怎样的方程？
设去年购买计算机x台.
设今年购买计算机x台.
解：合并同类项，得 系数化为1，得
例2.某工厂的产值连续增长，去年是前年的1.5倍，今年是去年的2倍，这三年总产值为550万元．前年的产值是多少？
分析：设前年的产值是x万元，根据题意可得去年的产值是1.5x万元，今年的产值是1.5x×2＝3x万元，根据这三年的总产值为550万元，列出方程求解即可．解：设前年的产值是x万元，由题意得x+1.5x+1.5x×2＝550，解得：x＝100．答：前年的产值是100万元．
分析实际问题中的数量关系，利用其中的相等关系列出方程建立数学模型，是解决实际问题的一种数学方法.
用方程解决实际问题的过程：
2.对方程 合并同类项正确的是( )
A. B. C. D.
3.方程 的解是( )
A. B. C. D.
解：合并同类项，得−?=? 系数化为1，得 ?=−?
解：合并同类项，得 ??=? 系数化为1，得 ?=?
5、有一列数，按一定规律排列成1，－3，9，－27，81，－243，···，其中某三个相邻数的和是－1 701，这三个数各是多少？
（1）你今天学习的解方程有哪些步骤？
（2）解方程中合并同类项和系数化为1的作用分别是什么？蕴含了什么数学思想？