
2023-2024学年福建省泉州市晋江市磁灶中学等校联考高二(下)期末数学试卷(含解析)
展开一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合M={−2,−1,0,1,2},N={x|−x2+x+6≤0},则M∩N=( )
A. {−2}B. {2}C. {−2,−1,0,1}D. {0,1,2}
2.若i(1−z)=1,则z+z−=( )
A. −2B. −1C. 1D. 2
3.已知空间中不过同一点的三条直线l,m,n.“l,m,n共面”是“l,m,n两两相交”的( )
A. 充分不必要条件 B. 既不充分也不必要条件 C. 充分必要条件 D. 必要不充分条件
4.已知α为锐角,csα=1+ 54,则sinα2=( )
A. 3− 58B. −1+ 58C. 3− 54D. −1+ 54
5.已知a>1,b>1,a=b3,则lga+3lgb10的最小值为( )
A. 4B. 6C. 8D. 10
6.甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演,若甲不站在两端,丙和丁相邻,则不同的排列方式共有( )
A. 12种B. 24种C. 36种D. 48种
7.已知向量a=(2,1),a+b=(1,4),则向量a在b方向上的投影向量为( )
A. 1 10bB. −1 10bC. −110bD. 110b
8.已知a,b,c∈(0,1),且a−5=lna−ln5,b−4=lnb−ln4,c−3=lnc−ln3,则a,b,c的大小关系是( )
A. b
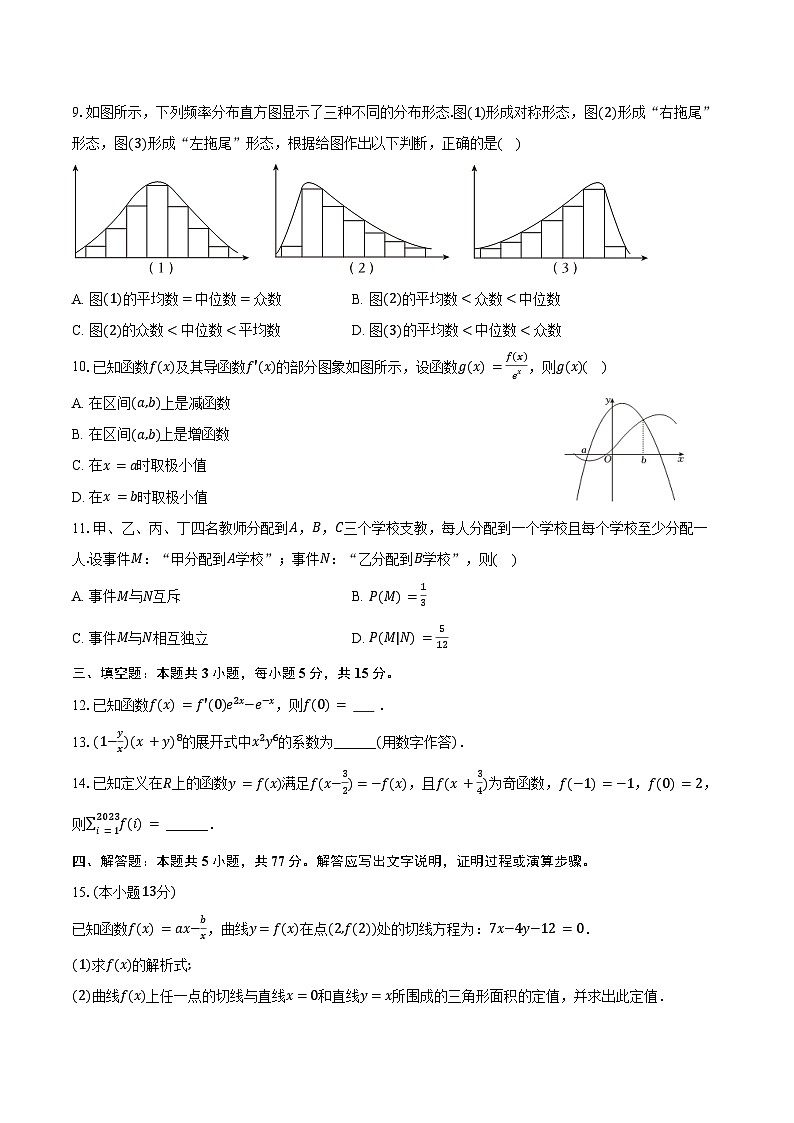
9.如图所示,下列频率分布直方图显示了三种不同的分布形态.图(1)形成对称形态,图(2)形成“右拖尾”形态,图(3)形成“左拖尾”形态,根据给图作出以下判断,正确的是( )
A. 图(1)的平均数=中位数=众数B. 图(2)的平均数<众数<中位数
C. 图(2)的众数<中位数<平均数D. 图(3)的平均数<中位数<众数
10.已知函数f(x)及其导函数f′(x)的部分图象如图所示,设函数g(x)=f(x)ex,则g(x)( )
A. 在区间(a,b)上是减函数
B. 在区间(a,b)上是增函数
C. 在x=a时取极小值
D. 在x=b时取极小值
11.甲、乙、丙、丁四名教师分配到A,B,C三个学校支教,每人分配到一个学校且每个学校至少分配一人.设事件M:“甲分配到A学校”;事件N:“乙分配到B学校”,则( )
A. 事件M与N互斥B. P(M)=13
C. 事件M与N相互独立D. P(M|N)=512
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数f(x)=f′(0)e2x−e−x,则f(0)= .
13.(1−yx)(x+y)8的展开式中x2y6的系数为______(用数字作答).
14.已知定义在R上的函数y=f(x)满足f(x−32)=−f(x),且f(x+34)为奇函数,f(−1)=−1,f(0)=2,则i=12023f(i)= ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知函数f(x)=ax−bx,曲线y=f(x)在点(2,f(2))处的切线方程为:7x−4y−12=0.
(1)求f(x)的解析式;
(2)曲线f(x)上任一点的切线与直线x=0和直线y=x所围成的三角形面积的定值,并求出此定值.
16.(本小题15分)
已知△ABC的内角A,B,C所对的边分别为a,b,c,f(x)=4csxsin(x−π6)的最大值为f(A).
(1)求角A;
(2)若点D在BC上,满足BC=3DC,且AD= 7,AB= 3,解这个三角形.
17.(本小题15分)
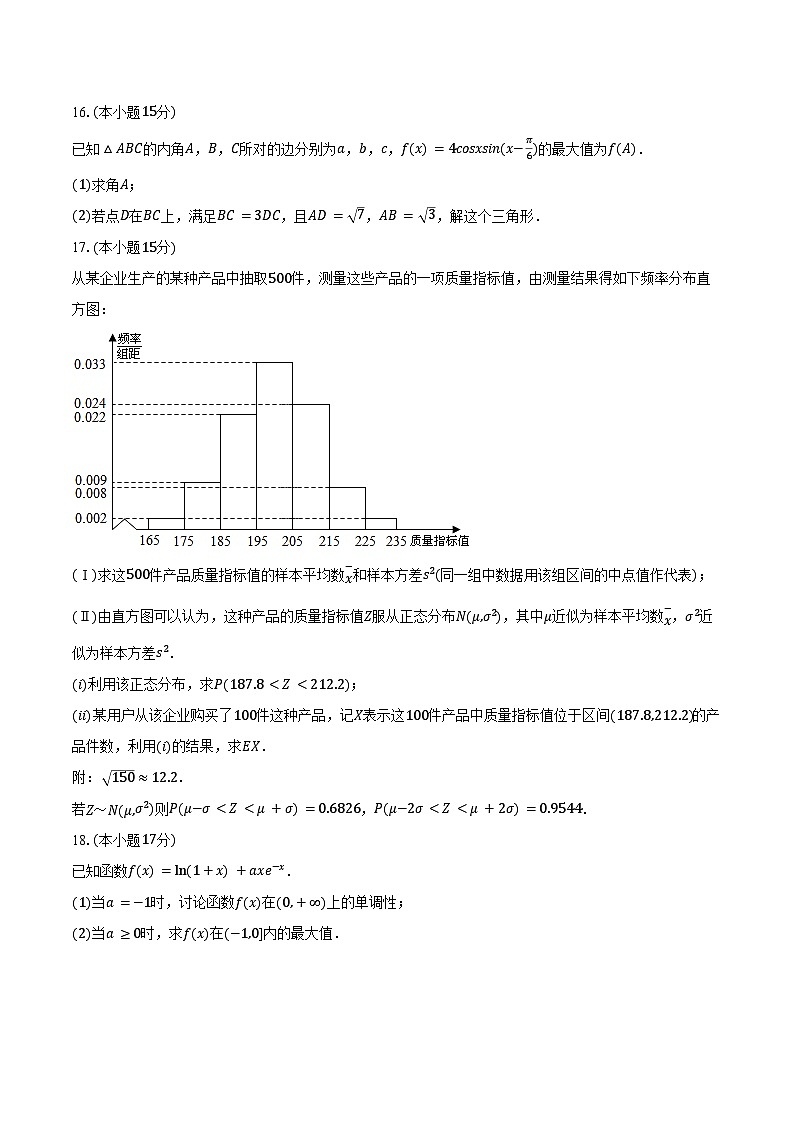
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
(Ⅰ)求这500件产品质量指标值的样本平均数x−和样本方差s2(同一组中数据用该组区间的中点值作代表);
(Ⅱ)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数x−,σ2近似为样本方差s2.
(i)利用该正态分布,求P(187.8
附: 150≈12.2.
若Z~N(μ,σ2)则P(μ−σ
已知函数f(x)=ln(1+x)+axe−x.
(1)当a=−1时,讨论函数f(x)在(0,+∞)上的单调性;
(2)当a≥0时,求f(x)在(−1,0]内的最大值.
19.(本小题17分)
为考察药物M对预防疾病A以及药物N对治疗疾病A的效果,科研团队进行了大量动物对照试验.根据100个简单随机样本的数据,得到如表联表:(单位:只)
(1)依据α=0.1的独立性检验,分析药物M对预防疾病A的有效性;
(2)用频率估计概率,现从患病的动物中用随机抽样的方法每次选取1只,用药物N进行治疗.已知药物N的治愈率如下:对未服用过药物M的动物治愈率为12,对服用过药物M的动物治愈率为34.若共选取3次,每次选取的结果是相互独立的.记选取的3只动物中被治愈的动物个数为X,求X的分布列和数学期望.
附:χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),n=a+b+c+d.
答案解析
1.A
【解析】解:∵−x2+x+6≤0,∴x2−x−6≥0,(x−3)(x+2)≥0,∴x≥3或x≤−2,
N={x|x≥3或x≤−2},M={−2,−1,0,1,2},则M∩N={−2}.
故选:A.
2.D
【解析】解:∵i(1−z)=1,
∴1−z=1i=−i,即z=1+i,
∴z+z−=1+i+1−i=2.
故选:D.
3.D
【解析】解:空间中不过同一点的三条直线l,m,n,
若“l,m,n两两相交”,则“l,m,n共面”,
反之不成立,l,m,n可能相互平行,
∴“l,m,n共面”是“l,m,n两两相交”的必要不充分条件,
故选:D.
4.D
【解析】解:csα=1+ 54,
则csα=1−2sin2α2,
故2sin2α2=1−csα=3− 54,即sin2α2=3− 58=( 5)2+12−2 516=( 5−1)216,
∵α为锐角,
∴sinα2>0,
∴sinα2=−1+ 54.
故选:D.
5.B
【解析】解:∵a>1,b>1,∴lga>0,lgb>0,
又∵a=b3,∴lga+3lgb10=3lgb+3lgb≥6,当且仅当lgb=1lgb,即b=10时取等号,
∴lga+3lgb10的最小值为6.
故选:B.
6.B
【解析】解:把丙和丁捆绑在一起,4个人任意排列,有A22⋅A44=48种情况,
甲站在两端的情况有33C21AA22=24种情况,
∴甲不站在两端,丙和丁相邻的不同排列方式有48−24=24种,
故选:B.
7.D
【解析】解:因为向量a=(2,1),a+b=(1,4),所以b=(−1,3),
向量a在b方向上的投影向量为a⋅b|b|⋅b|b|=−2+31+9b=110b.
故选:D.
8.C
【解析】解:a−5=lna−ln5,b−4=lnb−ln4,c−3=lnc−ln3,即a−lna=5−ln5,b−lnb=4−ln4,c−lnc=3−ln3,
令f(x)=x−lnx,x∈(0,+∞),则f′(x)=1−1x=x−1x,
由f′(x)=0得x=1,由f′(x)>0得x>1,由f′(x)<0得0
又f(a)=f(5),f(b)=f(4),f(c)=f(3),5>4>3>1,
则f(5)>f(4)>f(3),即f(a)>f(b)>f(c),
∵a,b,c∈(0,1),
∴a
9.ACD
【解析】解:图(1)的分布直方图是对称的,所以平均数=中位数=众数,A正确;
图(2)众数最小,右拖尾平均数大于中位数,B错误,C正确;
图(3)左拖尾众数最大,平均数小于中位数,D正确.
故选:ACD.
10.BC
【解析】解:由图象知,当x
已知g(x)=f(x)ex,函数定义域为R,
可得g′(x)=f′(x)−f(x)ex,
因为ex>0,
所以当x
当x>b时,g′(x)=f′(x)−f(x)ex<0,g(x)单调递减,
所以函数g(x)在x=a处取得极小值,在x=b处取得极大值,
故选:BC.
11.BD
【解析】解:对于A,甲分配到A学校的事件与乙分配到B学校的事件可以同时发生,即事件M与N不互斥,A错误;
对于B,甲分配到A,B,C三个学校是等可能的,则P(M)=13,B正确;
对于C,由选项B知,P(N)=13,P(MN)=1+C21C21C42A33=536,显然P(MN)≠P(M)P(N),
因此事件M与N相互不独立,C错误;
对于D,由选项BC知,P(M|N)=P(MN)P(N)=53613=512,D正确.
故选:BD.
12.−2
【解析】解:由函数f(x)=f′(0)e2x−e−x求导得:f′(x)=2f′(0)e2x+e−x,当x=0时,f′(0)=2f′(0)+1,解得f′(0)=−1,
因此f(x)=−e2x−e−x,
所以f(0)=−2.
故答案为:−2.
13.−28
【解析】解:由已知可得(1−yx)(x+y)8=(x+y)8−yx(x+y)8,
所以由二项式定理可得多项式(1−yx)(x+y)8的展开式中含x2y6的项为C86x2y6−yxC85x3y5=−28x2y6,
(1−yx)(x+y)8的展开式中x2y6的系数为−28.
故答案为:−28.
14.−1
【解析】解:∵f(x−32)=−f(x),①
∴f(x−3)=f(x),即f(x+3)=f(x),②
∴定义在R上的函数y=f(x)是以3为周期的函数.
又f(x+34)为奇函数,
∴函数y=f(x)关于点(34,0)成中心对称,
∴f(x)+f(32−x)=0,③
由①②得:f(−1)=−f(−52)=−f(12)=−1,
∴f(12)=1,代入③,有f(1)=−1.
∴f(−1)+f(0)+f(1)=−1+2−1=0.
∴i=12023f(i)=674×(f(1)+f(2)+f(3))+f(1)=f(1)=−1.
故答案为:−1.
15.解:(1)求导函数可得:f′(x)=a+bx2,
∵曲线y=f(x)在点(2,f(2))处的切线方程为7x−4y−12=0.
∴f(2)=12,f′(2)=74,
∴2a−b2=12,a+b4=74,
∴a=1,b=3,
∴f(x)的解析式为f(x)=x−3x;
(2)设(x0,x0−3x0)为曲线f(x)上任一点,则切线的斜率为1+3x02,
∴切线方程为y−(x0−3x0)=(1+3x02)(x−x0),
令x=0,可得y=−6x0,
由切线方程与直线y=x联立,求得交点横坐标为x=2x0,
∴曲线f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值12×|2x0|×|−6x0|=6.
【解析】(1)求导函数,利用曲线y=f(x)在点(2,f(2))处的切线方程为7x−4y−12=0,建立方程,可求得a=1,b=3,从而可得f(x)的解析式;
(2)求出切线方程,从而可计算切线与直线x=0和直线y=x所围成的三角形面积.
16.解:(1)由f(x)=4csxsin(x−π6)⇒f(x)=4csx(sinxcsπ6−csxsinπ6)=2 3sinxcsx−2cs2x= 3sin2x−(cs2x+1)=2sin(2x−π6)−1.
由三角函数的性质,可得2A−π6=π2+2kπ,即A=π3+kπ(k∈Z),
结合A∈(0,π),取k=0,得A=π3;
(2)如图所示,可得AD=AB+BD=AB+23BC=AB+23(AC−AB)=13AB+23AC,
所以AD2=49b2+2×29bccs∠BAC+19c2⇒7=49b2+2 39b+13⇒b=2 3(舍负),
由余弦定理得a2=b2+c2−2bccs∠BAC=12+3−6=9,解得a=3,
由此可得a2+c2=12=b2,所以B=π2,C=π2−A=π6.
综上所述,a=3,b=2 3,c= 3,∠BAC=π3,B=π2,C=π6.
【解析】(1)根据三角恒等变换公式化简f(x)表达式,然后利用三角函数的性质与特殊角的三角函数值,求出角A的大小;
(2)根据平面向量的基本定理、向量数量积的公式,求得AC长,再利用余弦定理求得BC长,最后由勾股定理的逆定理判断出角B、C的大小,可得答案.
17.解:(Ⅰ)抽取产品的质量指标值的样本平均数x−和样本方差s2分别为:
x−=170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
s2=(−30)2×0.02+(−20)2×0.09+(−10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.
(Ⅱ)(i)由(Ⅰ)知Z~N(200,150),从而P(187.8
依题意知X~B(100,0.6826),所以EX=100×0.6826=68.26.
【解析】(Ⅰ)根据频率分布直方图的数据,即可求出;
(Ⅱ)(i)由(Ⅰ)知Z~N(200,150),从而求出P(187.8
18.解:(1)当a=−1时,f(x)=ln(1+x)−xex,f′(x)=ex+x2−1(1+x)ex,且(1+x)ex>0,
当x>0时,ex>1,x2>0,则ex+x2−1>0,即f′(x)>0,
故函数f(x)在(0,+∞)上单调递增;
(2)f′(x)=11+x+a(1−x)ex=ex+a(1−x2)(1+x)ex,
令Q(x)=ex+a(1−x2),则Q′(x)=ex−2ax,
由x∈(−1,0]且a≥0,可得−2ax≥0,ex>0,则Q′(x)>0,Q(x)在(−1,0]内单调递增,
所以Q(x)>Q(−1)=1e>0,
又当x∈(−1,0]时,(1+x)ex>0,
所以f′(x)>0,f(x)在(−1,0]内单调递增,
故f(x)max=f(0)=0.
【解析】(1)根据求导公式和运算法则可得f′(x)=ex+x2−1(1+x)ex,由x>0可得(1+x)ex>0,ex+x2−1>0,即可求解;
(2)由题意可得f′(x)=ex+a(1−x2)(1+x)ex=Q(x)(1+x)ex,利用导数讨论函数Q(x)的性质可得Q(x)>0,进而f′(x)>0,则f(x)在(−1,0]内单调递增,即可求解.
19.解:(1)零假设H0:药物M对预防疾病A无效果,
补充完整的列联表如下所示:
所以χ2=100×(30×10−15×45)275×25×45×55=10033≈3.030>2.706,
根据小概率值α=0.1的独立性检验,我们推断零假设不成立,即认为药物M对预防疾病A有效果.
(2)设A表示药物N的治愈率,B1表示未服用过药物M且患病,B2表示服用过药物M且患病,
由题意得,P(B1)=1525=0.6,P(B2)=1025=0.4,且P(A|B1)=0.5,P(A|B2)=0.75,
所以P(A)=P(B1)×P(A|B1)+P(B2)×P(A|B2)=0.6×0.5+0.4×0.75=0.6,
即药物N的治愈率p=0.6=35,
所以X~B(3,35),
所以P(X=0)=C30(25)3=8125,P(X=1)=C31(35)1(25)2=36125,P(X=2)=C32(35)2(25)1=54125,P(X=3)=C33(35)3=27125,
所以随机变量X的分布列如下表所示:
数学期望E(X)=0×8125+1×36125+2×54125+3×27125=95.
【解析】(1)提出零假设H0,计算χ2的值,并与附表中的数据进行对比,即可作出判断;
(2)利用全概率公式求出药物N的治愈率p=35,利用X~B(3,35),结合二项分布的概率公式与数学期望的计算方法,求解即可.药物M
疾病A
合计
未患病
患病
未服用
15
45
服用
45
合计
25
α
0.100
0.050
0.010
0.001
xα
2.706
3.841
6.635
10.828
药物M
疾病A
合计
未患病
患病
未服用
30
15
45
服用
45
10
55
合计
75
25
100
x
0
1
2
3
P
8125
36125
54125
27125
2023-2024学年福建省福州市多校联考高二(下)期末数学试卷(含解析): 这是一份2023-2024学年福建省福州市多校联考高二(下)期末数学试卷(含解析),共14页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省泉州市晋江市五校联考高二(下)期末数学试卷(含详细答案解析): 这是一份2022-2023学年福建省泉州市晋江市五校联考高二(下)期末数学试卷(含详细答案解析),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年福建省平山中学、内坑中学、磁灶中学、永春二中、永和中学高一上学期期中联考数学试题(含解析): 这是一份2023-2024学年福建省平山中学、内坑中学、磁灶中学、永春二中、永和中学高一上学期期中联考数学试题(含解析),共13页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












