还剩9页未读，
继续阅读
2023-2024学年黑龙江省齐齐哈尔市龙江县八年级（下）期末数学试卷（含答案）
展开这是一份2023-2024学年黑龙江省齐齐哈尔市龙江县八年级（下）期末数学试卷（含答案），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列各式是最简二次根式的是( )
A. 12B. 0.2C. 2D. 20
2.在下列四组数中，属于勾股数的是( )
A. 1，2，3B. 1， 2， 3C. 4，5，6D. 5，12，13
3.下列计算正确的是( )
A. 3+ 7= 10B. 5 3− 3=5
C. 8÷2= 4D. (−3)×(−6)=3 2
4.在下列给出的条件中，能判定四边形ABCD为平行四边形的是( )
A. AB//CD，AD=BC B. ∠A=∠B，∠C=∠D
C. AO=OC，DO=OB D. AB=AD，CB=CD
5.在射击选拔赛中，选手甲、乙、丙、丁各射击10次，平均环数与方差情况如表所示.若要从中选拔一名成绩较好且发挥稳定的选手参加运动会，则最终入选的选手是( )
A. 甲B. 乙C. 丙D. 丁
6.关于一次函数y=−2x+2，下列结论不正确的是( )
A. 图象与直线y=−2x平行B. 图象与y轴的交点坐标是(1,0)
C. 图象经过第一、二、四象限D. y随自变量x的增大而减小
7.小明学了在数轴上表示无理数的方法后，进行了练习：首先画数轴，原点为O，在数轴上找到表示数2的点A，然后过点A作AB⊥OA，使AB=1；再以O为圆心，OB的长为半径作弧，交数轴正半轴于点P，那么点P表示的数是( )
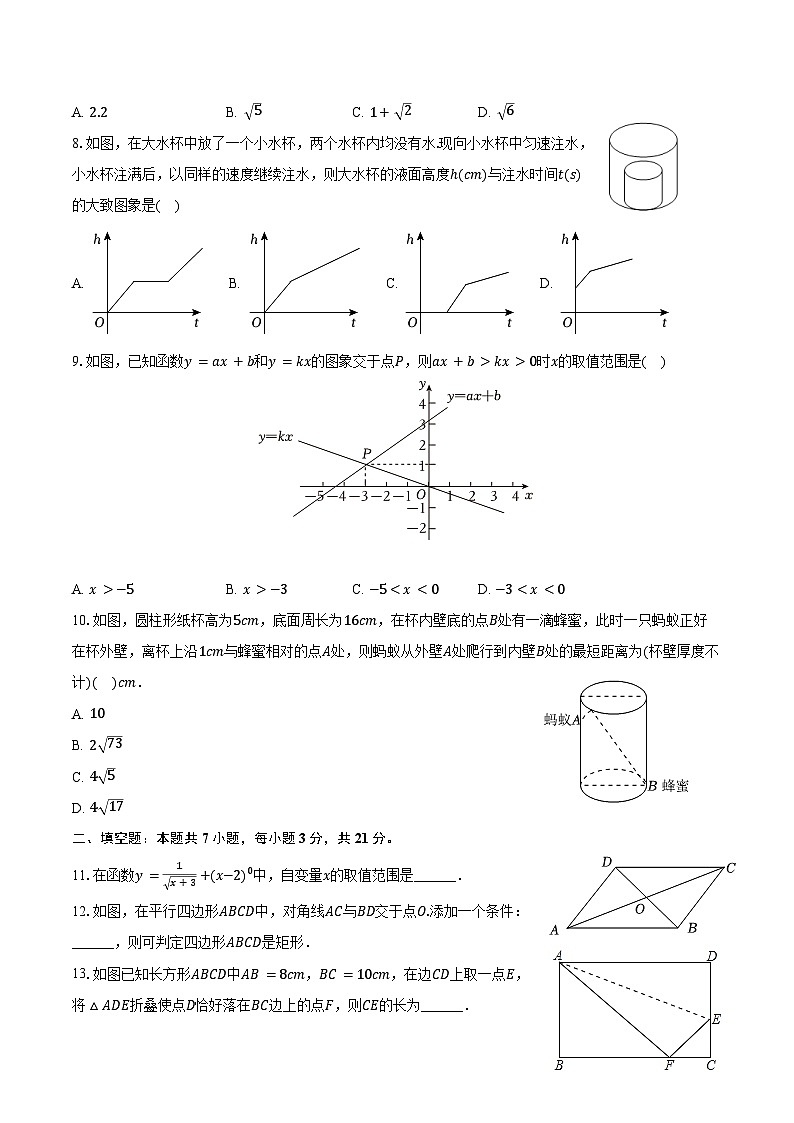
A. 2.2B. 5C. 1+ 2D. 6
8.如图，在大水杯中放了一个小水杯，两个水杯内均没有水.现向小水杯中匀速注水，小水杯注满后，以同样的速度继续注水，则大水杯的液面高度ℎ(cm)与注水时间t(s)的大致图象是( )
A. B. C. D.
9.如图，已知函数y=ax+b和y=kx的图象交于点P，则ax+b>kx>0时x的取值范围是( )
A. x>−5B. x>−3C. −5
A. 10
B. 2 73
C. 4 5
D. 4 17
二、填空题：本题共7小题，每小题3分，共21分。
11.在函数y=1 x+3+(x−2)0中，自变量x的取值范围是______．
12.如图，在平行四边形ABCD中，对角线AC与BD交于点O.添加一个条件：______，则可判定四边形ABCD是矩形．
13.如图已知长方形ABCD中AB=8cm，BC=10cm，在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，则CE的长为______．
14.如图，在∠MON的两边上分别截取OA，OB，使OA=OB；分别以点A，B为圆心，OA长为半径作弧，两弧交于点C；连接AC，BC，AB，OC.若AB=2cm，四边形OACB的面积为4cm2.则OC的长为______cm．
15.已知点(−3,y1)，(1,y2)，(−2,y3)都在直线y=2x−1上，则y1，y2，y3的大小关系是______．
16.如图，O为坐标原点，四边形OABC为矩形，A(20,0)，C(0,8)，D为OA的中点，点P在边BC上运动，当PD=OD时，点P的坐标为______．
17.已知，如图，点A1为x轴上一点，它的坐标为(1,0)，过点A1作x轴的垂线与直线OM：y=x交于点B1，以线段A1B1为边作正方形A1B1C1A2；延长A2C1交直线OM于点B2，再以线段A2B2为边作正方形A2B2C2A3；延长A3C2交直线OM于点B3，再以线段A3B3为边作正方形A3B3C3A4…依此类推，C2024的
坐标为______．
三、解答题：本题共7小题，共69分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题10分)
计算：
(1) 24÷ 3− 13× 6+ 32；
(2)(2023−π)0+ 32÷ 8−|1− 3|−(12)−2．
19.(本小题9分)
为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查，设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组：x<8.5；B组：8.5≤x<9；C组：9≤x<9.5；D组：9.5≤x<10；E组：x≥10．
根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：
(1)本次共调查了______名学生；
(2)补全条形统计图；
(3)在本次调查的数据的中位数落在第______组；
(4)若该校有4500名学生，请估计该校睡眠时间不足9小时的学生有多少名？
20.(本小题9分)
小乐是一个善于思考的学生，学习完“二次根式”和“勾股定理”后，他发现可以有多种方法求三角形的面积，以下是他的数学笔记，请认真阅读并完成任务，
(1)请根据思路1的公式，求△ABC的面积；
(2)请你结合思路2，在如图所示的网格中(正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点)，完成下列任务，
①画出△ABC，要求三个顶点都在格点上；
②结合图形，写出△ABC面积的计算过程．
21.(本小题10分)
如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE//AC，且DE=12AC，连接CE．
(1)求证：四边形OCED为矩形；
(2)连接AE，若BD=6，AE= 73，求菱形ABCD的周长．
22.(本小题11分)
2024年4月25日，搭载神舟十八号载人飞船的长征二号F遥十八运载火箭，在酒泉卫星发射中心点火升空，将航天员叶光富、李聪和李广苏顺利送入太空，神舟十八号载人飞船发射取得圆满成功.某航天模型销售店看准商机，推出“神舟”和“天宫”模型.已知销售店老板购进2个“神舟”模型和4个“天宫”模型一共需要100元；购进3个“神舟”模型和2个“天宫”模型一共需要90元．
(1)分别求每个“神舟”模型和“天宫”模型的进货价格；
(2)该销售店计划购进两种模型共100个，且“神舟”模型的数量不超过“天宫”模型数量的一半.若每个“神舟”模型的售价为40元，每个“天宫”模型的售价为30元，则购进多少个“神舟”模型时，销售这批模型的利润最大？最大利润是多少元？
23.(本小题10分)
下面是某项目化学习小组的部分学习过程再现，请阅读并解答问题．
【童话故事】“龟兔赛跑”讲述了这样的故事：兔子和乌龟从起点同时出发，领先的兔子看着缓慢爬行的乌龟，骄傲起来，在路边小树处睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟先到达了终点．
【分组探究】
A组成员用x表示兔子和乌龟从起点出发所行的时间，y1、y2分别表示兔子和乌龟所行的路程，画出了能大致表示上面故事情节的图象，如图1．
根据图1回答下列问题：
(1)赛跑的全程是______米，乌龟比兔子早到达终点______分钟；
(2)乌龟在这次比赛中的平均速度是______米/分钟；
(3)求兔子睡醒后的函数解析式.(不需要写自变量取值范围)
【故事改编】
B组成员对童话故事进行了改编：兔子输了比赛，心里很不服气，它们约定再次赛跑，兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑，乌龟、兔子的速度及赛场均和A组的数据一致，它们同时出发，结果兔子先到达了终点，小组成员根据故事情节绘制如图2的图象．
根据图2回答问题：
(4)图2中，自变量x表示兔子和乌龟所行的时间，y1、y2分别表示兔子和乌龟所行的路程，在乌龟行进过程中，请直接写出当兔子出发多长时间，乌龟和兔子相距100米？
24.(本小题10分)
【问题情境】神奇的半角模型
在几何图形中，共顶点处的两个角，其中较小的角是较大的角的一半时，我们称之为半角模型.截长补短法是解决这类问题常用的方法．
如图1，在正方形ABCD中，以A为顶点的∠EAF=45°，AE、AF与BC、CD分别交于E、F两点，为了探究EF、BE、DF之间的数量关系，小明的思路如下：
如图2，延长CB到点H，使BH=DF，连接AH，先证明△ADF≌△ABH，再证明△AHE≌△AFE.从而得到EF、BE、DF之间的数量关系．
(1)提出问题：EF、BE、DF之间的数量关系为______．
(2)知识应用：如图3，AB=AD，∠B=∠D=90°，以A为顶点的∠BAD=120°，∠EAF=60°，AE、AF与BC、CD分别交于E、F两点，你认为(1)中的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．
(3)知识拓展：如图4，在四边形ABCD中，AB=AD=a，BC=b，CD=c.∠ABC与∠D互补，AE、AF与BC、CD分别交于E、F两点，且∠EAF=12∠BAD，请直接写出△EFC的周长= ______.(用含a、b、c的式子表示.)
参考答案
1.C
2.D
3.D
4.C
5.A
6.B
7.B
8.C
9.D
10.A
11.x>−3且x≠2
12.AC=BD(或∠DAB=90°)(答案不唯一，正确即可)
13.3cm
14.4
15.y1
17.(22024,22023)
18.解：(1)原式= 24÷3− 13×6+4 2
=2 2− 2+4 2
=5 2；
(2)原式=1+ 32÷8+1− 3−4
=1+2+1− 3−4
=− 3．
19.(1)100；
(2)补全条形统计如下：
(3)C；
(4)4500×40100=1800(人)，
答：估计该校睡眠时间不足9小时的学生有1800名．
20.解：(1)由题意，得S△ABC= 14[a2b2−(a2+b2−c22)2]
= 14[42×( 5)2−(42+( 5)2−( 13)22)2]
=4．
(2)①如图，△ABC即为所求．(画法不唯一)
②过点A作AD⊥CB于点D，由题意，得AD=2．
∴S△ABC=12CB⋅AD=12×4×2=4．
21.(1)证明：∵四边形ABCD是菱形，
∴AC⊥BD，AO=OC=12AC，
∴∠DOC=90°，
∵DE//AC，DE=12AC，
∴DE=OC，DE//OC，
∴四边形OCED是平行四边形，
又∵∠DOC=90°，
∴平行四边形OCED是矩形；
(2)解：由(1)可知，平行四边形OCED是矩形，
∴∠ECA=90°，EC=OD=12BD=3，DE=OC=12AC，
由勾股定理可得，AC= AE2−EC2= 73−9=8，
∴OC=4，
∴DC= OC2+OD2= 42+32=5，
∴菱形ABCD的周长=5×4=20．
22.解：(1)设每个“神舟”模型的进货价格为x元，每个“天宫”模型的进货价格为y元．
由题意得2x+4y=1003x+2y=90，
解得x=20y=15．
答：每个“神舟”模型的进货价格为20元，每个“天宫”模型的进货价格为15元．
(2)设购进m个“神舟”模型，(100−m)个“天宫”模型时，销售这批模型的利润最大，最大利润为w元．
由题意得，w=(40−20)m+(30−15)(100−m)=5m+1500．
m≤12(100−m)，解得，m≤1003，
∵5>0，
∴w随m的增大而增大．由题意知，m取整数．
∴当m=33时，w取得最大值，为5×33+1500=1665(元)．
∴当购进33个“神舟”模型时，销售这批模型的利润最大，最大利润为1665元．
23.(1)1200，10；
(2)20；
(3)设兔子睡醒后的函数解析式为y=kx+b，
把(50,400)，(70,1200)代入得：
50k+b=40070k+b=1200，
解得k=40b=−1600，
∴兔子睡醒后的函数解析式为y=40x−1600；
(4)由图象可得，乌龟的速度为(1200−400)÷40=20(米/分钟)，兔子的速度为1200÷30=40(米/分钟)，
∴y1=40x，y2=400+20x，
∵乌龟和兔子相距100米，
∴|40x−(400+20x)|=100，
即20x−400=100或20x−400=−100，
解得x=25或x=15，
∴当兔子出发25分钟或15分钟，乌龟和兔子相距100米．
24.(1)EF=DF+BE；
(2)成立，理由如下：延长CB到点G，使BG=DF，连接AG，
∵AB=AD，∠ABG=∠D，
∵BG=DF，
∴△ADF≌△ABG(SAS)，
∴AG=AF，∠GAB=∠DAF，
∵∠EAF=60°，∠BAD=120°，
∴∠BAE+∠DAF=60°，
∴∠GAE=60°，
∵AE=AE，
∴△AGE≌△AFE(SAS)．
∴GE=EF，
∴EF=DF+BE；
(3)b+c．
选手
甲
乙
丙
丁
平均环数
9.0
9.0
8.8
8.8
方差
0.41
0.52
0.41
0.52
题目：已知在△ABC中，AC= 5,BC=4,AB= 13，求△ABC的面积，
思路1：可以利用八年级下册课本16页“阅读与思考”中的海伦−秦九韶公式求△ABC的面积，海伦公式，S= p(p−a)(p−b)(p−c)，其中p=12(a+b+c)，
秦九韶公式，S= 14[a2b2−(a2+b2−c22)2]，
思路2：可以利用勾股定理在正方形网格中构造三角耏，将△ABC的面积．
相关试卷
2023-2024学年黑龙江省齐齐哈尔市龙江县数学八上期末联考试题含答案：
这是一份2023-2024学年黑龙江省齐齐哈尔市龙江县数学八上期末联考试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，4的平方根是，如图，中的周长为等内容，欢迎下载使用。
2022-2023学年黑龙江省齐齐哈尔市龙江县七年级（下）期末数学试卷（含解析）：
这是一份2022-2023学年黑龙江省齐齐哈尔市龙江县七年级（下）期末数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年黑龙江省齐齐哈尔市龙江县八年级（下）期末数学试卷（含解析）：
这是一份2022-2023学年黑龙江省齐齐哈尔市龙江县八年级（下）期末数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
