2023-2024学年广西贵港市桂平市八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年广西贵港市桂平市八年级（下）期末数学试卷（含答案），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.已知：点P的坐标为(−1,2)，则点P所在的象限是( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
2.下面图形中，是中心对称图形的是( )
A. B. C. D.
3.我们把每一组数的频数与数据总数的比叫作这一组数据的频率(relative frequency).在“relative”中，字母“e”出现的频率是( )
A. 14B. 18C. 38D. 12
4.由线段a，b，c组成的三角形是直角三角形的是( )
A. a=2，b=3，c=4B. a=3，b=4，c=5
C. a=4，b=5，c=6D. a=6，b=8，c=11
5.在平面直角坐标系中，点P(−5,3)关于x轴对称的点的坐标为( )
A. (5,3)B. (5,−3)C. (−5,−3)D. (3,−5)
6.一个n边形的内角和为720°，则n等于( )
A. 4B. 5C. 6D. 7
7.下列图象中，表示y不是x的函数的是( )
A. B. C. D.
8.将直线y=2x−1向上平移4个单位，可得到直线( )
A. y=2x+3B. y=2x+4C. y=−2x−4D. y=−2x+3
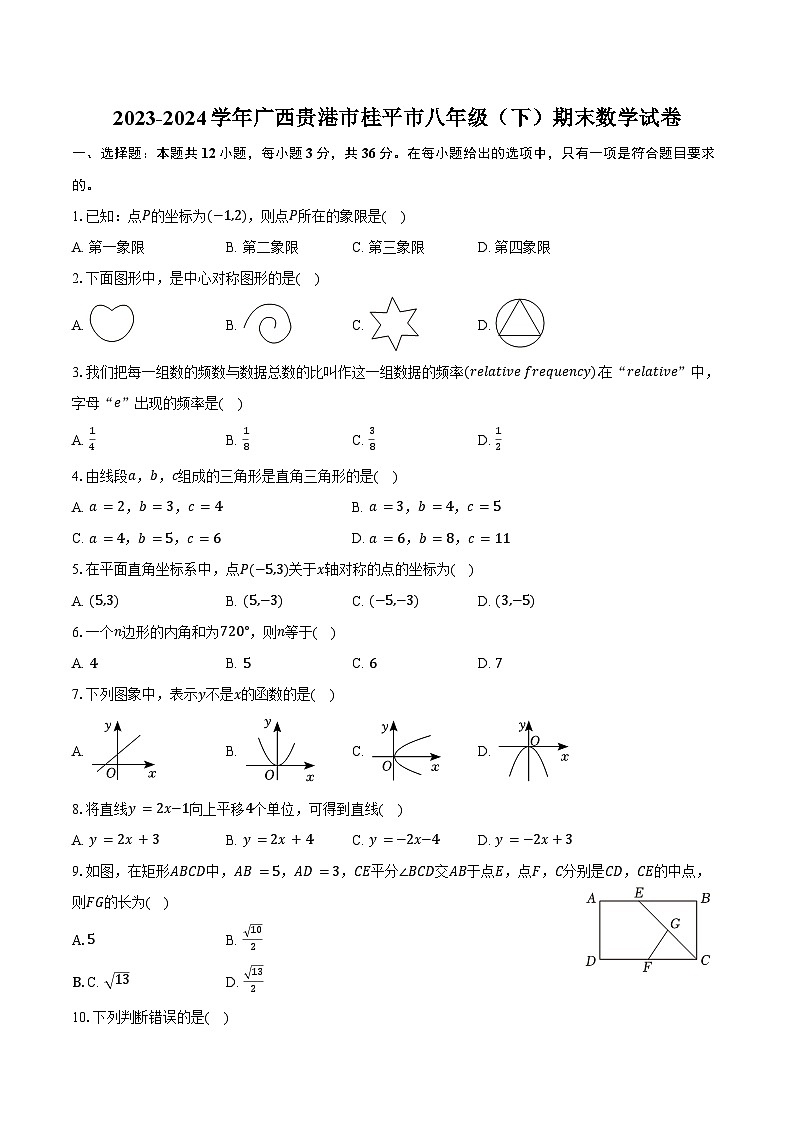
9.如图，在矩形ABCD中，AB=5，AD=3，CE平分∠BCD交AB于点E，点F，C分别是CD，CE的中点，则FG的长为( )
5B. 102
C. 13D. 132
10.下列判断错误的是( )
A. 对角线互相垂直且相等的平行四边形是正方形 B. 对角线相等且互相平分的四边形是矩形
C. 对顶角相等 D. 同旁内角互补
11.某星期日上午10：00，小星从家匀速步行到附近的图书馆，看完书后他匀速跑步回家，已知跑步的速度是步行速度的2倍，如图表示小星离家的距离y(千米)与所用的时间x(分钟)之间的关系，下列说法正确的是( )
A. 小星在图书馆看书的时间是70分钟
B. 小星家与图书馆的距离为4千米
C. 小星的步行速度是5千米/小时
D. 小星回到家的时刻是上午11：25
12.如图，在正方形ABCD中，AB=4，AC与BD相交于点O，N是AO的中点，点M在边上，且BM=3，P为对角线BD上一点，当对角线BD平分∠NPM时，|PM−PN|的值为( )
A. 1
B. 2
C. 2
D. 3
二、填空题：本题共6小题，每小题2分，共12分。
13.分解因式：x2−3x=______．
14.正比例函数y=kx(k≠0)的图象经过点A(−1,5)，则k=______．
15.在Rt△ABC中，D是斜边AB的中点，若AB=13，则DC的长是______．
16.设矩形的一条对角线长为2cm，两条对角线组成的对顶角中，有一组是120°，则矩形的周长是______．
17.在“探索一次函数y=kx+b的系数k，b与图象的关系”活动中，老师给出了直角坐标系中的三个点：A(0,2)，B(2,3)，C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象，并得到对应的函数表达式y1=k1x+b1，y2=k2x+b2，y3=k3x+b3.分别计算k1+b1，k2+b2，k3+b3的值，其中最大的值等于______．
18.如图，在菱形ABCD中，∠A=60°，AB=4，动点E、F分别在线段AB、BC上，且BE=CF，则EF的最小值为______．
三、解答题：本题共8小题，共72分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题6分)
计算：(−3)2÷[2−(−7)]+6×(−13)．
20.(本小题6分)
已知T=4n(n−2m)−(m−2n)2+m2．
(1)化简T；
(2)若m，n是菱形ABCD两条对角线的长，且该菱形的面积为6，求T的值．
21.(本小题10分)
如图，已知△ABC三个顶点的坐标分别为A(−3,2)，B(−4,−2)，C(0,−3)，将△ABC先向右平移5个单位．再向下平移3个单位，它的像是△A1B1C1．
(1)请画出△A1B1C1，并直接写出点A1的坐标；
(2)△ABC外有一点M经过同样的平移后得到点M1(5,3)，直接写出点M的坐标；
(3)连接线段MM1，AA1，则这两条线段之间的关系是______．
22.(本小题10分)
如图，已知函数y1=3x+b和y2=ax−2的图象交于点P(−1,−4)，这两个函数的图象与x轴分别交于点A、B．
(1)分别求出这两个函数的解析式；
(2)求△ABP的面积；
(3)根据图象直接写出不等式3x+b+2≤ax的解集．
23.(本小题10分)
已知：如图，在▱ABCD中，点E，F分别为AB、CD的中点，BD是对角线，AG//DB交CB的延长线于G．
(1)求证：DE=FB；
(2)若四边形DEBF是菱形，求证：四边形AGBD是矩形．
24.(本小题10分)
某校八年级学生进行了一次视力调查，绘制出频数分布表和频数直方图的一部分如下．
请根据图表信息回答下列问题：
(1)在频数分布表中，a的值为______，b的值为______．
(2)将频数直方图补充完整；
(3)甲同学说“我的视力情况是此次抽样调查所得数据的中位数”，问甲同学的视力情况在哪个范围内？
(4)若视力在4.9以上(含4.9)均属正常，求视力正常的人数占被调查人数的百分比．
25.(本小题10分)
如图，在△ABC中，∠C=90°，∠ABC=60°，以点B为圆心、任意长为半径画圆弧分别交边AB，BC于点E，F，再分别以点E，F为圆心，以大于12EF的长为半径画圆弧，两弧相交于点G，连接BG并延长交AC于点D．
(1)求证：BD平分∠ABC；
(2)若AD=4，求△BCD的周长．
26.(本小题10分)
综合与实践
【模型探索】如图1，在正方形ABCD中，点E，F分别在边DC，BC上，若AF⊥BE，则AF与BE的数量关系为______；
【模型应用】如图2，将边长为2的正方形ABCD折叠，使点B落在CD边的中点E处，点A落在点F处，折痕交AD于点M，交BC于点N，求折痕MN的长度；
【迁移应用】如图3，正方形ABCD的边长为12，点F是BC上一点，将△ABF沿AF折叠，使点B落在点B′处，连接BB′；并延长交CD于点E.若CE=5，求EB′的长度．
参考答案
1.B
2.C
3.A
4.B
5.C
6.C
7.C
8.A
9.D
10.D
11.D
12.A
13.x(x−3)
14.−5
15.6.5
16.(2+2 3)cm
17.5
18.2 3
19.解：原式=9÷(2+7)−2
=9÷9−2
=1−2
=−1．
20.解：(1)T=4n(n−2m)−(m−2n)2+m2
=4n2−8mn−m2+4mn−4n2+m2
=−4mn．
(2)∵m，n是菱形ABCD两条对角线的长，且该菱形的面积为6，
∴12mn=6，
∴mn=12，
∴T=−4mn=−4×12=−48．
21.(1)如图，△A1B1C1即为所求，A1(2,−1)．
(2)由题意M(0,5)．
(3)AA1=MM1，AA1//MM1
22.解：(1)∵将点P(−1,−4)代入y1=3x+b，得−4=3×(−1)+b，
解得b=−1；
将点P(−1,−4)代入y2=ax−2，得−4=a×(−1)−2，
解得a=2，
∴这两个函数的解析式分别为y1=3x−1和y2=2x−2；
(2)∵在y1=3x−1中，令y1=0，得x=13，
∴A(13,0)．
∴OA=13，
∵在y2=2x−2中，令y2=0，得x=1，
∴B(1,0)．
∴OB=1，
∴AB=OB−OA=1−13=23，
∴S△ABP=12AB×4=12×23×4=43；
(3)∵3x+b+2≤ax，
∴3x+b≤ax−2，
由函数图象可知，当x≤−1时，3x+b≤ax−2．
∴当x≤−1时，3x+b+2≤ax．
23.(1)证明：∵四边形ABCD是平行四边形，
∴AD//BC，∠BAD=∠C，AD=CB，AB=CD，
∵点E，F分别是AB，CD的中点，
∴AE=12AB，CF=12CD，
∴AE=CF．
在△ADE和△CBF中，AD=CB∠EAD=∠CAE=CF，
∴△ADE≌△CBF(SAS)，
∴DE=FB；
(2)证明：∵AD//BC，AG//DB，
∴四边形AGBD是平行四边形，
∵四边形BEDF是菱形，
∴BE=DE=AE=12AB，
∴△ABD是直角三角形，∠ADB=90°，
∴四边形AGBD是矩形．
24.解：(1)抽取的总人数是：20÷0.1=200(人)，
则a=200×0.3=60(人)，
b=1−0.1−0.2−0.35−0.3=0.05，
故答案为：60，0.05．
(2)根据(1)求出的数据，补全频数分布直方图如下：
(3)中位数落在第3组内，甲同学的视力情况在4.6≤x<4.9范围内；
(4)视力正常的人数占被调查人数的百分比是60+10200×100%=35%．
25.(1)证明：连接FG，EG，
由作图知，BE=BF，FG=EG，
在△BEG与△BFG中，
BE=BFFG=EGBG=BG，
∴△BEG≌△BFG(SSS)，
∴∠FBG=∠EBG，
∴BD平分∠ABC；
(2)解：∵∠C=90°，∠ABC=60°，
∴∠A=180°−90°−60°=30°，
∵BD平分∠ABC；
∴∠ABD=∠CBD=12∠ABC=30°，
∴∠A=∠ABD，
∴AD=BD=4，
∴CD=12BD=2，
∴BC= BD2−CD2=2 3，
∴△BCD的周长=BD+CD+BC=4+2+2 3=6+2 3．
26.【模型探索】AF=BE；
【模型应用】如图2，过C作CP//MN交AD于P，
∵将边长为2的正方形ABCD折叠，使点B落在CD边的中点E处，
∴点B与点E关于MN对称，
∴BE⊥MN，
∴CP⊥BE，
∵点E是CD边的中点，
∴CE=12CD=1，
∴BE= BC2+CE2= 5，
由【模型探索】知CP=BE= 5，
∵AD//BC，CP//MN，
∴四边形CPMN是平行四边形，
∴MN=CP= 5；
【迁移应用】∵四边形ABCD是正方形，
∴∠C=90°，
∵BC=12，CE=5，
∴BE= BC2+CE2=13，
∵将△ABF沿AF折叠，使点B落在点B′处，
∴点B与点B′关于AF对称，
∴BE⊥AF于H，BB′=2BH，
由【模型探索】知，AF=BE=13，BF=CE=5，
∵S△ABF=12AB⋅BF=12AF⋅BH，
∴BH=AB⋅BFAF=12×513=6013，
∴BB′=12013，
∴EB′=13−12013=4913．
视力
频数(人)
频率
4.0≤x<4.3
20
0.1
4.3≤x<4.6
40
0.2
4.6≤x<4.9
70
0.35
4.9≤x<5.2
a
0.3
5.2≤x<5.5
10
b