




高考一轮复习 高三数学知识点专题讲解1 集合课件PPT
展开强基础 固本增分
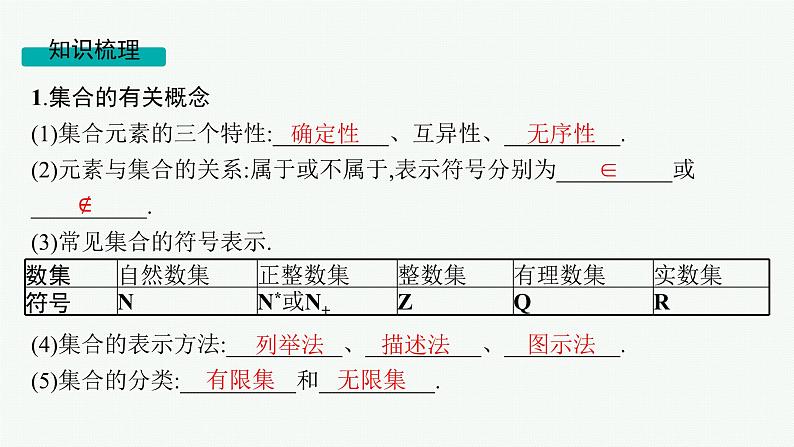
1.集合的有关概念(1)集合元素的三个特性:__________、互异性、__________. (2)元素与集合的关系:属于或不属于,表示符号分别为__________或__________. (3)常见集合的符号表示.
(4)集合的表示方法:__________、__________、__________. (5)集合的分类:__________和__________.
微点拨空集的本质是集合中不含有任何元素,但其表现形式却是多种多样的,它与方程、不等式有着密切的联系,例如:集合{x|ax+1=0},{x|x2+x+a=0}, {x|a
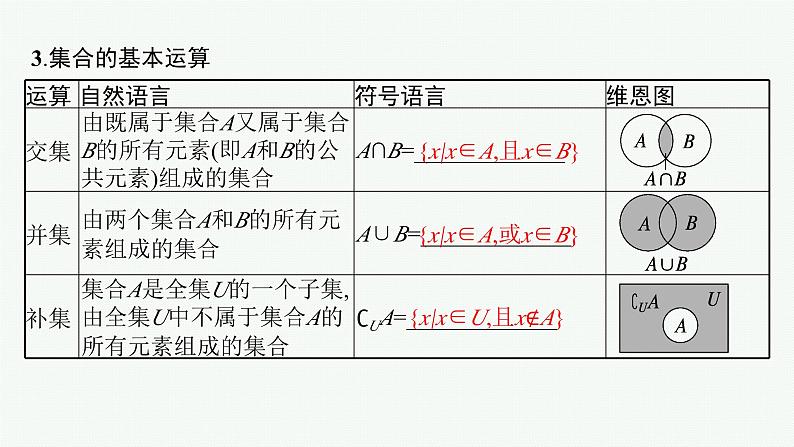
{x|x∈A,或x∈B}
{x|x∈U,且x∉A}
微点拨集合运算的性质(1)并集的性质:A∪⌀=⌀∪A=A;A∪A=A;A∪B=B∪A;A∪B=A⇔B⊆A.(2)交集的性质:A∩⌀=⌀∩A=⌀;A∩A=A;A∩B=B∩A;A∩B=A⇔A⊆B.(3)补集的性质:A∪(∁UA)=U;A∩(∁UA)=⌀;∁U(∁UA)=A;∁U(A∩B)=(∁UA)∪(∁UB); ∁U(A∪B)=(∁UA)∩(∁UB).
常用结论1.若非空集合A含有n个元素,则A有2n个子集,有(2n-1)个真子集,有(2n-2)个非空真子集.2.空集是任何集合的子集,是任何非空集合的真子集.3.等价关系:A⊆B⇔A∩B=A⇔A∪B=B⇔∁UA⊇∁UB.4.集合元素个数满足:card(A∪B)=card(A)+card(B)-card(A∩B).
题组一 思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.若3∈{0,1,x+2,x2-1},则实数x的值为1,-2,2.( )2.{x|y=3x-1}={y|y=3x-1}.( )3.集合A={x|ax-1=0}必有2个子集.( )4.若集合A是非空集合,且A∪B=A∪C,则B=C.( )5.若A∪B⊆A∩B,则必有A=B.( )
题组二 回源教材6.(人教B版必修第一册1.1.2练习B第2题改编)已知集合A={x|x=3m-1,m∈N}, B={x|x=3m+2,m∈N},则集合A与集合B之间的关系是__________.
7.(人教B版必修第一册1.1.3练习B第4题)设全集U={2,4,a2},集合A={4,a+3}, ∁UA={1},则实数a的值为__________.
解析 A={-1,2,5,8,…},B={2,5,8,11,…},所以B⫋A.
8.(人教A版必修第一册习题1.2第5题)已知集合A={x|0
解析 因为B⊆A,所以a≥2.
题组三 连线高考9.(2022·新高考Ⅱ,1)已知集合A={-1,1,2,4},B={x||x-1|≤1},则A∩B=( )A.{-1,2}B.{1,2}C.{1,4}D.{-1,4}
解析 B={x|0≤x≤2},则A∩B={1,2},故选B.
解析 ∵A⊆B,∴a-2=0或2a-2=0.若a-2=0,则a=2,A={0,-2},B={1,0,2},显然A⊈B;若2a-2=0,则a=1,A={0,-1},B={1,-1,0},A⊆B成立.故选B.
研考点 精准突破
考点一 集合的基本概念
例1(1)(2024·山东烟台模拟)已知集合A={1,3,m2-1},B={1,3,m+1},若A=B,则实数m等于( )A.-1或2B.0或1C.2D.-1
解析 因为A=B,所以m2-1=m+1,解得m=2或m=-1,当m=2时,B={1,3,3}不满足集合元素的互异性,舍去;当m=-1时,A={1,3,0},B={1,3,0}符合题意,故选D.
(3)(2024·河南开封模拟)已知A={x|x2-ax+1<0},若2∈A,且3∉A,则a的取值范围是( )
规律方法解决集合概念问题的解题技巧 (1)弄清集合中的元素类型,即确定集合是数集还 是点集,还是其他元素; (2)弄清楚集合元素满足的限制条件,确定元素的 属性; (3)注意检验集合中的元素是否满足互异性,确定 集合元素的个数.(4)弄清楚描述法表示的集合中相关字母变量的取 值范围及条件.
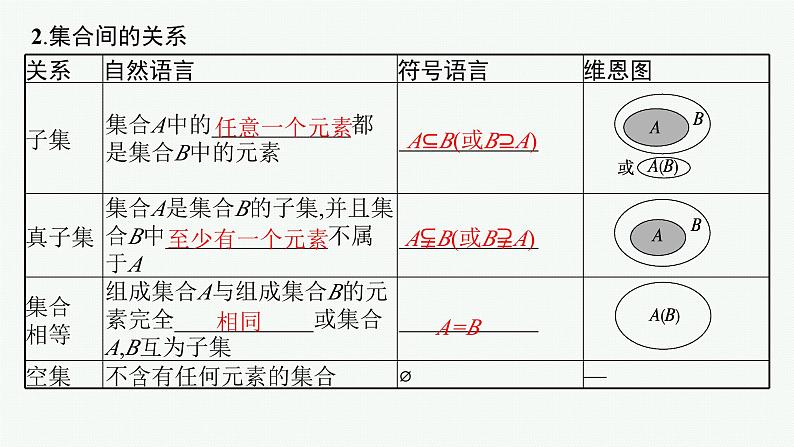
考点二 集合间的基本关系
例2(1)(2024·黑龙江哈尔滨模拟)集合A={x∈N|y=lg(4-x)}的子集个数为( )A.2B.4C.8D.16
解析 依题意,A={x∈N|x<4}={0,1,2,3},共有4个元素,所以其子集个数为24=16,故选D.
A.M⊆NB.M=NC.M⊇ND.M∩N=⌀
(3)(2024·山东德州模拟)已知集合A={x|x2-4≤0},B={x||x-a|<1},若B⊆A,则实数a的取值范围是( )A.(-1,1)B.[-1,1]C.[-1,1)D.(-1,1]
解析 由已知得A={x|x2-4≤0}={x|-2≤x≤2},B={x||x-a|<1}={x|a-1
解 由已知得A={x|x2-4<0}={x|-2
变式探究2若将本例(3)条件中的集合B改为B={x||x-1|
综上,实数a的取值范围是(-∞,1].
规律方法1.判断两集合关系的方法
2.根据两集合的关系求参数的方法(1)已知两个集合之间的关系求参数时,要明确集合中的元素,对含参数的集合是否为空集进行分类讨论,做到不漏解.(2)若集合中的元素是一一列举的,依据集合间的关系,转化为解方程(组)求解,此时注意集合中元素的互异性.(3)若集合表示的是不等式的解集,常依据数轴转化为不等式(组)求解,此时需注意端点值能否取到.
[对点训练1](2024·山东聊城模拟)已知集合A={x|0≤x≤2},B={x|a
考点三 集合的运算(多考向探究预测)
考向1 集合的基本运算例3(1)(2023·新高考Ⅰ,1)已知集合M={-2,-1,0,1,2},N={x|x2-x-6≥0},则M∩N=( )A.{-2,-1,0,1}B.{0,1,2}C.{-2}D.{2}
解析 由题意,x2-x-6≥0,解得x≤-2或x≥3,N=(-∞,-2]∪[3,+∞).因为M={-2,-1,0,1,2},所以M∩N={-2}.故选C.
(3)(2024·广东深圳模拟)已知A={x|y=ln(x+2)},B={y|y=sin x},则∁AB=( )A.(-2,-1]∪[1,+∞)B.(-2,-1]∪(1,+∞)C.(-2,-1)∪[1,+∞)D.(-2,-1)∪(1,+∞)
解析 因为A={x|y=ln(x+2)}={x|x>-2},B={y|y=sin x}={y|-1≤y≤1},则∁AB=(-2,-1)∪(1,+∞),故选D.
规律方法解集合运算问题的三个注意点
A.A∪B=AB.A∩B=BC.A∪B=BD.A∩B=⌀
解析 因为x2-3x-10<0,所以-2
考向2 利用集合的运算求参数值例4(2024·江苏无锡模拟)已知集合A={x∈Z|-1
[对点训练3](1)(2024·浙江金华模拟)已知集合A={x|lg(x+a)>0}, B={x|x2≥4},若A∪B=R,则实数a的取值范围是( )A.(3,+∞)B.(-1,+∞)C.[3,+∞)D.[-1,+∞)
解析 由已知得A={x|x>1-a},B={x|x≤-2或x≥2},又A∪B=R,所以1-a≤-2,即a≥3,故选C.
(2)(2024·山西太原模拟)已知A,B为非空数集,且A={0,1},(∁RA)∩B={-1},则符合条件的集合B的个数为( )A.1B.2C.3D.4
解析 因为(∁RA)∩B={-1},A={0,1},所以-1∈B,0可能属于B,1可能属于B,所以B={-1}或B={-1,0}或B={-1,1}或B={-1,1,0},故满足条件的集合B的个数为4,故选D.
考点四 Venn图的应用
例5(2024·广东汕头模拟)某年级先后举办了数学、历史、音乐的讲座,其中有85人听了数学讲座,70人听了历史讲座,61人听了音乐讲座,16人同时听了数学、历史讲座,12人同时听了数学、音乐讲座,9人同时听了历史、音乐讲座,还有5人听了全部讲座,则听讲座的人数为__________.
解析 将已知条件用Venn图表示出来如图所示,所以听讲座的人数为62+7+5+11+45+4+50=184.
规律方法Venn图解决集合中的元素个数问题在一些实际问题中,涉及有限集合的元素个数计算问题,这时依据题意画出 Venn图表示集合及集合的交、并、补集,直观简洁,事半功倍,在各个区域标出元素个数,然后利用容斥原理即可解决问题.
高考数学一轮复习题型讲解+专题训练(新高考专用)专题01集合(原卷版+解析): 这是一份高考数学一轮复习题型讲解+专题训练(新高考专用)专题01集合(原卷版+解析),共45页。试卷主要包含了【2022年新高考II卷】,【2022年全国甲卷理科】,【2022年全国乙卷文科】等内容,欢迎下载使用。
高考数学一轮复习知识点讲解+真题测试专题9.5抛物线(知识点讲解)(原卷版+解析): 这是一份高考数学一轮复习知识点讲解+真题测试专题9.5抛物线(知识点讲解)(原卷版+解析),共29页。
高考数学一轮复习知识点讲解+真题测试专题9.4双曲线(知识点讲解)(原卷版+解析): 这是一份高考数学一轮复习知识点讲解+真题测试专题9.4双曲线(知识点讲解)(原卷版+解析),共33页。












