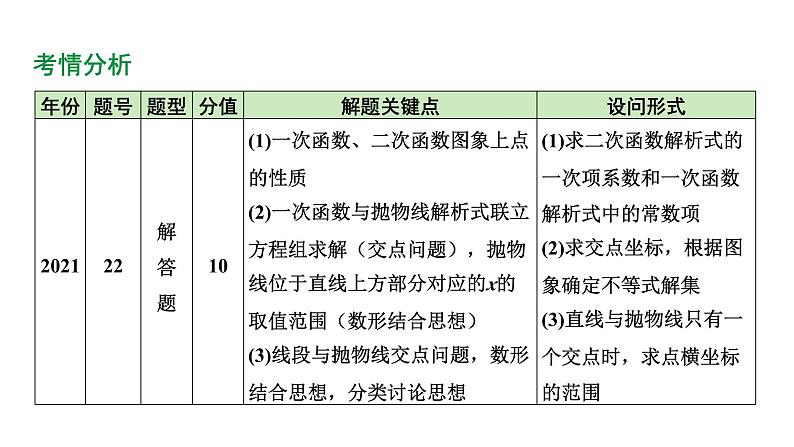
河南省2024年数学中考热点备考重难专题：二次函数图象与性质综合题交点问题（课件）

这是一份河南省2024年数学中考热点备考重难专题：二次函数图象与性质综合题交点问题（课件），共23页。PPT课件主要包含了课件说明，课堂练兵，课后小练，典例精讲，交点问题，考情分析等内容，欢迎下载使用。
一、课件设计初衷 基于老师在总复习过程中对重难题型有较大的需求，以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性，有助于学生题图结合梳理题意，理解平面图形的变化过程.二、课件亮点1.依据区域考情，针对性选题 按照本地区考情及考法选题，针对性强，有效提高老师备课效率2.贴近学生实际解题情境，形式符合教学习惯 审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注，帮助学生梳理关键信息，激发学生兴趣，调动积极性3.含解题思路引导与方法总结，提高课堂互动性 通过问题启发式解题思路点拨，激发学生数学思考与探索. 方法总结使学生复习一类题，会一类题，取得有效的复习成果三、课件使用场景适用于中考专题复习或题位复习
二次函数图象与性质综合题
(1)求抛物线的解析式及顶点坐标；
解：(1)∵抛物线y＝x2＋bx＋c交x轴于C，D两点，点C的坐标为(－1，0).对称轴为直线x＝1，∴∴抛物线的解析式为y＝x2－2x－3＝(x－1)2－4，∴抛物线的顶点坐标为(1，－4)；
(2)当－1≤x≤2时，求y的取值范围；
先画出抛物线对称轴x＝1
自变量取值在对称轴同侧，还是异侧，
开口向上，自变量在对称轴异侧，在顶点处y取值最小，离对称轴较远的端点处，y值最大
－1≤x≤2在对称轴异侧
(2)∵抛物线开口向上，顶点坐标为(1，－4)，∴函数最小值为y＝－4，对称轴为直线x＝1，∵|－1－1|＞|2－1|，∴当x＝－1时，y＝1＋2－3＝0为函数最大值，∴当－1≤x≤2时，y的取值范围是－4≤y≤0；
(3)连接AB，若抛物线y＝x2＋bx＋c向下平移k(k＞0)个单位时，与线段AB只有一个公共点，结合函数图象，直接写出k的取值范围．
观察图形你发现了什么？
①抛物线顶点在线段AB上
练习题 已知：抛物线y＝x2－2x＋3a＋1(a为常数)．(1)当a＝1时，求该抛物线的顶点坐标；
解：(1)当a＝1时，抛物线的顶点坐标为(1，3)；
y＝x2－2x＋1＋3a化为顶点式，将a＝1直接代入
练习题 已知：抛物线y＝x2－2x＋3a＋1(a为常数)．
(2)抛物线上有两点M(－1，yM)，N(2，yN)，请比较yM与yN的大小；
异侧：离对称轴的距离或利用对称性转化到同侧比较大小
确定两点与对称轴的关系（同侧/异侧）
同侧：结合增减性，判断；
(2)易知抛物线的对称轴为直线x＝1，∵抛物线开口向上，且1－(－1)＝2，2－1＝1，2＞1，∴yM＞yN；
(3)在平面直角坐标系中，若该抛物线在x≤3的部分与直线y＝2x－3有两个交点，求a的取值范围．
看到交点问题，想到什么方法？
有两个交点，说明什么？
联立的一元二次方程中b2－4ac＞0
另外，别忘了x≤3！
练习1 如图，已知抛物线y＝x2＋bx＋c分别交x轴、y轴于点A(－1，0)，C(0，－3)，连接AC.
(1)求抛物线的解析式；
(2)∵y＝x2－2x－3＝(x－1)2－4，∴抛物线开口向上，对称轴为直线x＝1，将x＝－2代入y＝x2－2x－3得y＝5，∴抛物线经过(－2，5)，∵点(－2，5)关于对称轴的对称点为(4，5)，y1≥y2，∴－2≤m＜m＋1≤4，解得－2≤m≤3；
(2)若P(x1，y1)，Q(x2，y2)是抛物线上两点，当x1≤－2，m≤x2≤m＋1时，均有y1≥y2，求m的取值范围；
(3)将该抛物线向左平移n(n＞0)个单位长度后，得到一条新抛物线，若新抛物线与线段AC只有一个交点，请直接写出n的取值范围．
【解法提示】由题意得新抛物线的解析式为y＝(x－1＋n)2－4，当新抛物线过点C(0，－3)时，将其代入得(0－1＋n)2－4＝－3，解得n＝2或n＝0(舍去)，当新抛物线过点A(－1，0)时，将其代入得(－1－1＋n)2－4＝0，解得n＝4或n＝0(舍去)，∴当新抛物线与线段AC只有一个交点时，n的取值范围为2≤n≤4.
练习2 (2022河南预测卷)在平面直角坐标系中，二次函数y＝x2＋bx＋c的图象过(－2，0)，(4，0)两点．(1)求二次函数的解析式；
练习2 (2022河南预测卷)在平面直角坐标系中，二次函数y＝x2＋bx＋c的图象过(－2，0)，(4，0)两点．
(2)当－1≤x≤5时，求函数值的取值范围；
(2)∵y＝x2－2x－8＝(x－1)2－9，∴抛物线的对称轴为直线x＝1.当x＝1时，y有最小值－9.∵5－1＞1－(－1)，∴当x＝5时，y有最大值，y最大＝(5－1)2－9＝7.∴当－1≤x≤5时，函数值的取值范围为－9≤y≤7；
(3)一次函数y＝(3＋m)x＋6＋2m的图象与二次函数y＝x2＋bx＋c的图象的交点的横坐标分别为x1，x2，且x1＜5＜x2，求m的取值范围．
(3)∵y＝(3＋m)x＋6＋2m＝(3＋m)(x＋2)，∴一次函数y＝(3＋m)x＋6＋2m的图象过定点(－2，0).又∵x＝－2时，y＝x2－2x－8＝(－2)2－2×(－2)－8＝0，∴x1＝－2.∵x2＞5，∴当x＝5时，一次函数的图象在二次函数图象的上方，