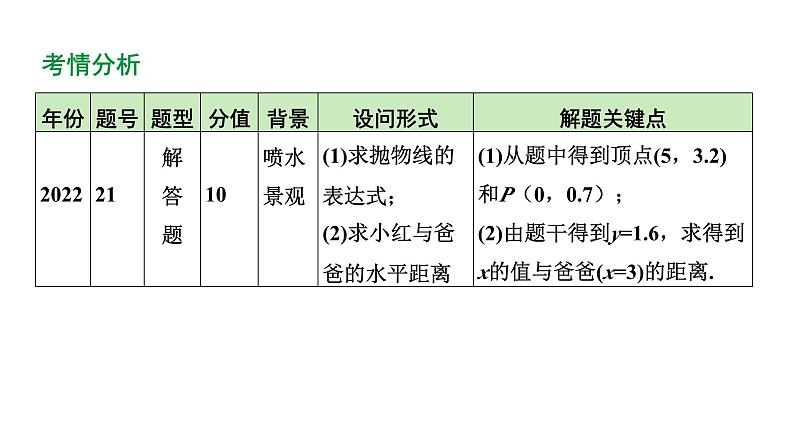
河南省2024年数学中考热点备考重难专题：抛物线型实际应用题（课件）

这是一份河南省2024年数学中考热点备考重难专题：抛物线型实际应用题（课件），共24页。PPT课件主要包含了课件说明，抛物线型实际应用题，课堂练兵，课后小练，典例精讲，考情分析，方法总结等内容，欢迎下载使用。

一、课件设计初衷 基于老师在总复习过程中对重难题型有较大的需求，以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性，有助于学生题图结合梳理题意，理解平面图形的变化过程.二、课件亮点1.依据区域考情，针对性选题 按照本地区考情及考法选题，针对性强，有效提高老师备课效率2.贴近学生实际解题情境，形式符合教学习惯 审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注，帮助学生梳理关键信息，激发学生兴趣，调动积极性3.含解题思路引导与方法总结，提高课堂互动性 通过问题启发式解题思路点拨，激发学生数学思考与探索. 方法总结使学生复习一类题，会一类题，取得有效的复习成果三、课件使用场景适用于中考专题复习或题位复习
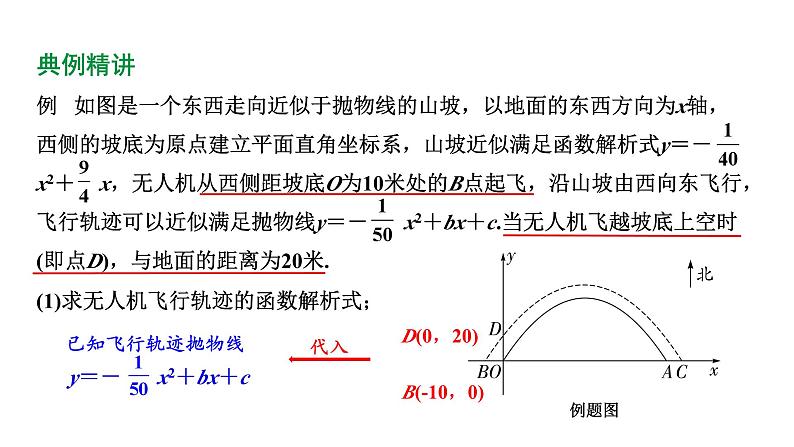
(1)求无人机飞行轨迹的函数解析式；
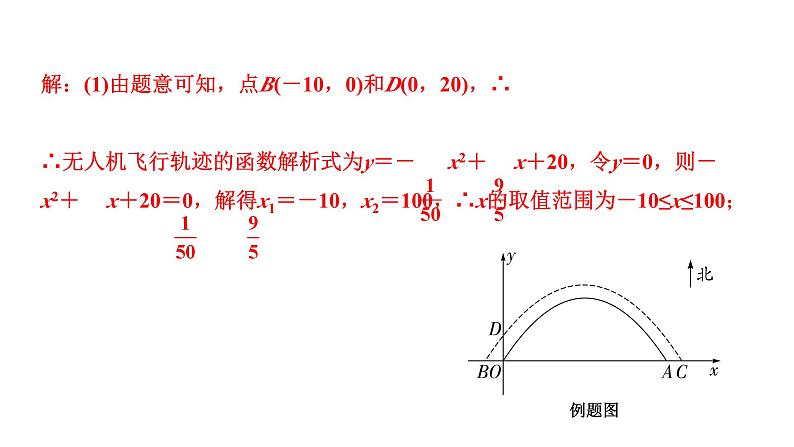
解：(1)由题意可知，点B(－10，0)和D(0，20)，∴∴无人机飞行轨迹的函数解析式为y＝－ x2＋ x＋20，令y＝0，则－ x2＋ x＋20＝0，解得x1＝－10，x2＝100，∴x的取值范围为－10≤x≤100；
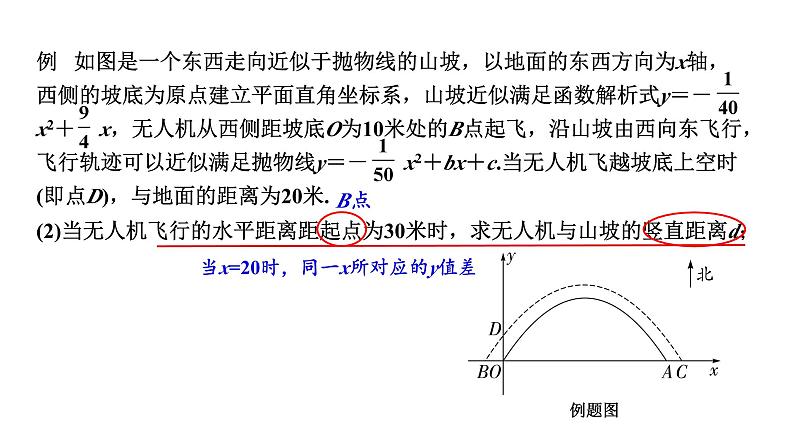
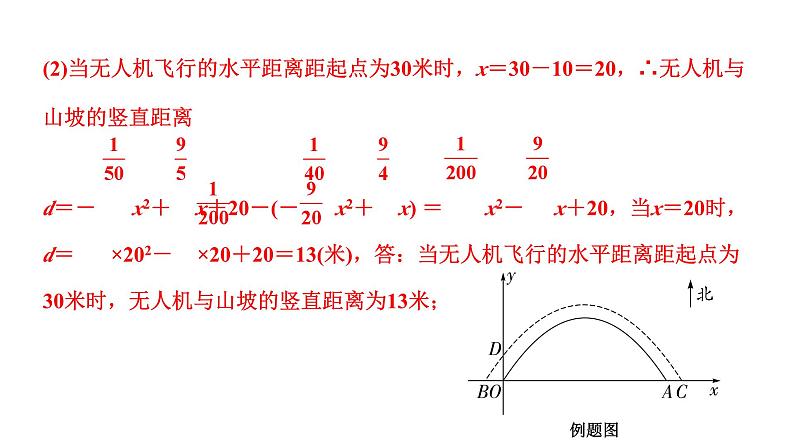
(2)当无人机飞行的水平距离距起点为30米时，求无人机与山坡的竖直距离d；
当x=20时，同一x所对应的y值差
(2)当无人机飞行的水平距离距起点为30米时，x＝30－10＝20，∴无人机与山坡的竖直距离d＝－ x2＋ x＋20－(－ x2＋ x) ＝ x2－ x＋20，当x＝20时，d＝ ×202－ ×20＋20＝13(米)，答：当无人机飞行的水平距离距起点为30米时，无人机与山坡的竖直距离为13米；
(3)由于山坡上有障碍物，无人机不能离山坡过近．当无人机与山坡的竖直距离大于9米时，无人机飞行才是安全的，请判断无人机此次飞行是否安全，并说明理由．
只要证明竖直距离d横大于9，即为安全
在解抛物线型实际应用时，解题的关键从情境入手，将题干中的信息转化为抛物线中的相关信息，一般为将距离转化为点位置（常需要分类讨论思想）和点坐标，再根据二次函数性质解题
求点坐标间距离水平距离：x轴上两点间的（水平）距离，图象上两点距y轴的距 离，实质是求两点横坐标之差的绝对值；竖直距离：两条抛物线上同一横坐标所对应y值之差；
是否安全通过类问题：判断两条抛物线上同一横坐标所对应y值之差是否大于定值，大于则能安全通过。
练习 如图1的某种发石车是古代一种远程攻击的武器，发射出去的石块的运动轨迹是抛物线的一部分，且距离发射点20米时达到最大高度10米．将发石车置于山坡底部O处，山坡上有一点A，点A与点O的水平距离为30米，与地面的竖直距离为3米，AB是高度为3米的防御墙．若以点O为原点，建立如图2的平面直角坐标系．(1)求石块运动轨迹所在抛物线的解析式；
根据已知信息设顶点式，代入原点坐标
练习 如图1的某种发石车是古代一种远程攻击的武器，发射出去的石块的运动轨迹是抛物线的一部分，且距离发射点20米时达到最大高度10米．将发石车置于山坡底部O处，山坡上有一点A，点A与点O的水平距离为30米，与地面的竖直距离为3米，AB是高度为3米的防御墙．若以点O为原点，建立如图2的平面直角坐标系．
(2)试通过计算说明石块能否飞越防御墙AB；
当x=30时，y值能否大于防御墙的高度（即点B的纵坐标）
(3)在竖直方向上，试求石块飞行时与坡面OA的最大距离．
第一步 表示距离 即为同一x下，两y值之差
(3)设直线OA的解析式为y＝kx(k≠0)，把(30，3)代入，得3＝30k，∴k＝ ．故直线OA的解析式为y＝ x．如图，设直线OA上方的抛物线上的一点P的坐标为(t，－ t2+t)，过点P作PQ⊥x轴，交OA于点Q，交x轴于点D，则Q(t， t)，∴PQ＝－ t2+t－ t＝－ t2+ t＝－ (t－18)2+8.1．∵二次项系数为负，∴图象开口向下，PQ有最大值∴当t＝18时，PQ取最大值，最大值为8.1．答：在竖直方向上，石块飞行时与坡面OA的最大距离是8.1米．
练习1 如今我国的大棚（如图1）种植技术已十分成熟．小明家的菜地上有一个长为16米的蔬菜大棚，其横截面顶部为抛物线型，大棚的一端固定在离地面高1米的墙体A处，另一端固定在离地面高2米的墙体B处，现对其横截面建立如图2所示的平面直角坐标系．已知大棚上某处离地面的高度y（米）与其离墙体A的水平距离x（米）之间的关系满足y＝﹣ x2+bx+c，现测得A，B两墙体之间的水平距离为6米．(1)直接写出b，c的值；
练习1 如今我国的大棚（如图1）种植技术已十分成熟．小明家的菜地上有一个长为16米的蔬菜大棚，其横截面顶部为抛物线型，大棚的一端固定在离地面高1米的墙体A处，另一端固定在离地面高2米的墙体B处，现对其横截面建立如图2所示的平面直角坐标系．已知大棚上某处离地面的高度y（米）与其离墙体A的水平距离x（米）之间的关系满足y＝﹣ x2+bx+c，现测得A，B两墙体之间的水平距离为6米．
(2)求大棚的棚顶到地面的距离；
(3)小明的爸爸欲在大棚内种植黄瓜，需搭建高为 米的竹竿支架若干，已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿，则共需要准备多少根竹竿？
(3)令y＝ ，则有 ，解得x1＝ ，x2＝ ，又∵0≤x≤6，∴大棚内可以搭建支架的土地的宽为6﹣ ＝ （米），又大棚的长为16米，∴需要搭建支架部分的土地面积为16× ＝88（平方米），故共需要88×4＝352（根）竹竿，答：共需要准备352根竹竿．
练习2 如图所示，一小球M从地面上的点O处抛出，球的抛出路线是抛物线的一部分，以过O的水平线为x轴，以过O且垂直于x轴的直线为y轴建立平面直角坐标系，OA是一个坡度为 的斜坡，若小球到达最高点的坐标为（4，8），（坡度：坡角的正切）(1)求抛物线的函数解析式；
练习2 如图所示，一小球M从地面上的点O处抛出，球的抛出路线是抛物线的一部分，以过O的水平线为x轴，以过O且垂直于x轴的直线为y轴建立平面直角坐标系，OA是一个坡度为 的斜坡，若小球到达最高点的坐标为（4，8），（坡度：坡角的正切）
(2)小球在斜坡上的落点A的垂直高度为多少米？