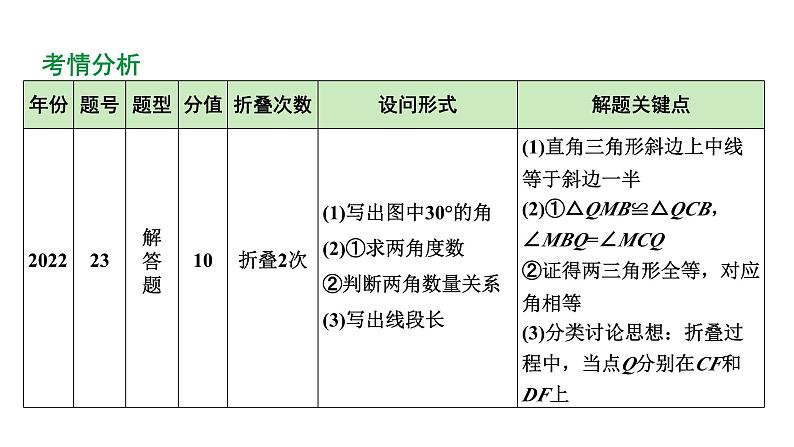
河南省2024年数学中考热点备考重难专题：综合与实践与折叠有关的探究（课件）

这是一份河南省2024年数学中考热点备考重难专题：综合与实践与折叠有关的探究（课件），共26页。PPT课件主要包含了课件说明，课堂练兵，课后小练，典例精讲，考情分析等内容，欢迎下载使用。

一、课件设计初衷 基于老师在总复习过程中对重难题型有较大的需求，以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性，有助于学生题图结合梳理题意，理解平面图形的变化过程.二、课件亮点1.依据区域考情，针对性选题 按照本地区考情及考法选题，针对性强，有效提高老师备课效率2.贴近学生实际解题情境，形式符合教学习惯 审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注，帮助学生梳理关键信息，激发学生兴趣，调动积极性3.含解题思路引导与方法总结，提高课堂互动性 通过问题启发式解题思路点拨，激发学生数学思考与探索. 方法总结使学生复习一类题，会一类题，取得有效的复习成果三、课件使用场景适用于中考专题复习或题位复习
综合与实践 与折叠有关的探究
例 (2022河南逆袭卷)综合与实践问题情境：如图，已知四边形ABCD是边长为2的菱形，且∠A＝60°，点E，F，G，H为四条边上的动点，且满足AE＝CH，AF＝CG，将菱形ABCD分别沿EF和GH折叠，点A的对应点为A′，点C的对应点为C′，连接A′G，C′F，得到四边形A′FC′G.
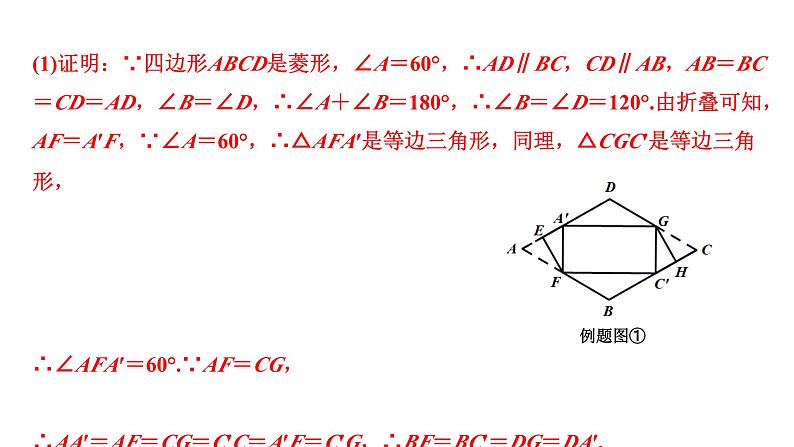
操作探究：(1)如图①，当点A′与点C′分别落在菱形ABCD的边AD和BC上时，求证：四边形A′FC′G是矩形；
矩形的判定定理有哪些？
①3个角是直角的四边形
②对角线相等的平行四边形
△EA′F≌△HC′G
△DA′G≌△BC′F
△CGC′为等边三角形
四边形A′FC′G是平行四边形
③有一个角为直角的平行四边形
题意可得∠A′FC′=90°
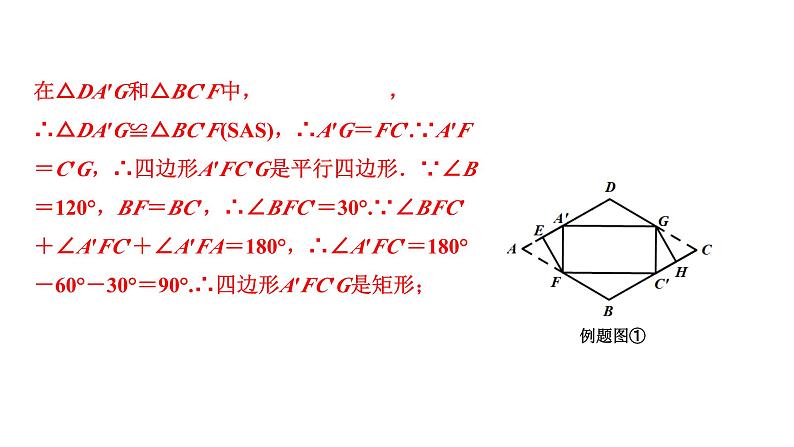
(1)证明：∵四边形ABCD是菱形，∠A＝60°，∴AD∥BC，CD∥AB，AB＝BC＝CD＝AD，∠B＝∠D，∴∠A＋∠B＝180°，∴∠B＝∠D＝120°.由折叠可知，AF＝A′F，∵∠A＝60°，∴△AFA′是等边三角形，同理，△CGC′是等边三角形，∴∠AFA′＝60°.∵AF＝CG，∴AA′＝AF＝CG＝C′C＝A′F＝C′G，∴BF＝BC′＝DG＝DA′.
在△DA′G和△BC′F中， ，∴△DA′G≌△BC′F(SAS)，∴A′G＝FC′.∵A′F＝C′G，∴四边形A′FC′G是平行四边形．∵∠B＝120°，BF＝BC′，∴∠BFC′＝30°.∵∠BFC′＋∠A′FC′＋∠A′FA＝180°，∴∠A′FC′＝180°－60°－30°＝90°.∴四边形A′FC′G是矩形；
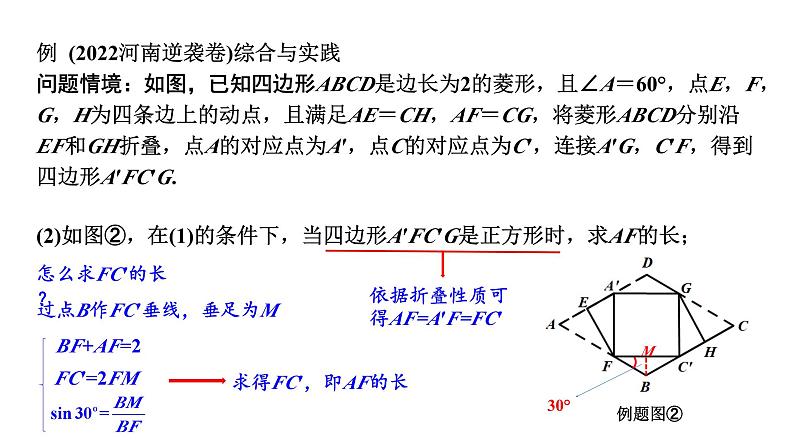
(2)如图②，在(1)的条件下，当四边形A′FC′G是正方形时，求AF的长；
依据折叠性质可得AF=A′F=FC′
过点B作FC′垂线，垂足为M
拓展延伸：(3)如图③，隐去右边折叠部分，若点F是AB边的中点，当A′F垂直于菱形ABCD的边时，请直接写出AE的长．
【解法提示】当A′F垂直于菱形ABCD的边时，分两种情况讨论如下：①如解图②，当A′F⊥AB，即A′F⊥CD时，∠AFA′＝90°，由折叠的性质得∠EFA＝∠A′FE＝45°，过点E作EG⊥AB于点G，则∠GEF＝45°，∴EG＝FG，设AG＝x，∵∠A＝60°，∴EG＝FG＝ x，AE＝2x，∵AB＝2，F是AB的中点，∴AF＝1，∴x＋ x＝1，解得x＝ ，∴AE＝ －1；②如解图③，当A′F⊥AD，即A′F⊥BC时，设A′F交AD于点H，则∠AHF＝90°，∵∠A＝60°，∴HF＝ AF＝ ，由折叠的性质得A′F＝AF＝1，∠A′＝∠A＝60°，∴A′H＝1－ ，∴AE＝A′E＝2A′H＝2－ .综上所述，AE的长为 －1或2－ .
练习 (2022河南定心卷)观察猜想(1)如图①，在矩形ABCD中，点E是BC的中点，将△DCE沿直线DE折叠后得到△DFE，点F在矩形ABCD的内部，延长DF交AB于点G，连接EG，猜想△DEG是直角三角形，请你证明这个猜想；
依据折叠性质得∠C=∠DFE=∠B
E是BC中点得EC=EF=BE
解： (1)∵四边形ABCD是矩形，∴∠B＝∠C＝90°，由折叠的性质得，∠DFE＝∠C＝90°，EC＝EF，∠CED＝∠FED，∴∠GFE＝90°＝∠B，∵E为BC的中点，∴BE＝EC，∴BE＝EF，∵EG＝EG，∴Rt△BEG≌Rt△FEG(HL)，∴∠BEG＝∠FEG，∵∠CED＝∠FED，∠BEC＝∠BEG＋∠FEG＋∠FED＋∠CED＝180°，∴∠GED＝∠FEG＋∠FED＝ ∠BEC＝90°，∴△DEG是直角三角形；
类比探究(2)若将图①中的矩形ABCD变为如图②的平行四边形，其他条件不变，那么(1)中的猜想是否仍然成立？请说明理由；
参考(1)中证明方法，证明△BEG≌△FEG
(2)(1)中的猜想仍成立，理由如下：
如解图，连接BF，∵四边形ABCD是平行四边形，∴∠ABC＋∠C＝180°，由折叠的性质得，∠DFE＝∠C，EC＝EF，∠CED＝∠FED，∵∠GFE＋∠DFE＝180°，∴∠ABC＝∠GFE，∵E为BC的中点，∴BE＝EC，
∴BE＝EF，∴∠EBF＝∠EFB，∴∠GBF＝∠GFB，∴GB＝GF，∵EG＝EG，∴△EBG≌△EFG(SSS)，∴∠BEG＝∠FEG，∵∠CED＝∠FED，∠BEC＝∠BEG＋∠FEG＋∠FED＋∠CED＝180°，∴∠GED＝∠FEG＋∠FED＝ ∠BEC＝90°，∴△DEG是直角三角形，(1)中的猜想仍然成立；
拓展延伸(3)在(2)的基础上，若∠ABC＝60°，AB＝6，G为AB边的三等分点，请直接写出BC的长．
【解法提示】如解图，过点G作GH⊥AD交DA的延长线于点H，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠HAG＝∠B＝60°.若G为AB边的三等分点，分两种情况讨论如下：①如解图①，此时AG＝ AB＝2，∴AH＝ AG＝1，GH＝ AG＝ ，由(2)得FG＝BG＝4，由折叠的性质得DF＝DC＝6，∴DG＝DF＋FG＝10，在Rt△DGH中，DG2＝DH2＋GH2，即102＝(1＋AD)2＋( )2，解得AD＝ －1(负值已舍去)，∴BC＝AD＝ －1；
练习 (2022甘肃黑白卷)如图是人教版八年级上册数学教材第79页的部分内容．把一张长方形的纸沿对角线折叠，重合部分是一个等腰三角形吗？为什么？
问题解决：(1)如图①，已知矩形ABCD(AB>AD)，将矩形纸片沿对角线AC折叠，使点B落在点P的位置，AP交CD于点Q.请判断△ACQ的形状，并进行证明；
解：(1)△ACQ是等腰三角形．证明：∵AB∥CD，∴∠BAC＝∠DCA，由折叠的性质可知∠BAC＝∠PAC，∴∠PAC＝∠DCA，∴QA＝QC，∴△ACQ是等腰三角形；
练习1 (2022甘肃黑白卷)如图是人教版八年级上册数学教材第79页的部分内容．把一张长方形的纸沿对角线折叠，重合部分是一个等腰三角形吗？为什么？
拓展延伸：(2)如图②，折叠矩形ABCD使点B落在CD上的点E处，折痕为GH，过点E作EF∥BC交GH于点F，连接BF，发现四边形BFEG是特殊四边形，请先写出是哪种特殊四边形，并进行证明；
(2)四边形BFEG是菱形．证明：由折叠的性质知GB＝GE，BF＝EF，∠BGF＝∠EGF.∵EF∥BC，∴∠BGF＝∠EFG，∴∠EGF＝∠EFG，∴EG＝EF，∴GB＝GE＝BF＝EF，∴四边形BFEG是菱形；
类比迁移：(3)在(2)的基础上，若AD＝6，AB＝10，当点E在CD边上移动时，折痕的端点G，H也随着移动，若限定G，H分别在线段BC，AB上移动，求四边形BFEG面积的变化范围．