函数模型及其应用课件- 高三数学一轮复习

这是一份函数模型及其应用课件- 高三数学一轮复习，共44页。PPT课件主要包含了学习目标，核心体系，活动方案，活动一基础训练，活动二典型例题，备用题等内容，欢迎下载使用。
1. 了解常见函数的性质.2. 了解常见函数模型在社会生活中的广泛应用．
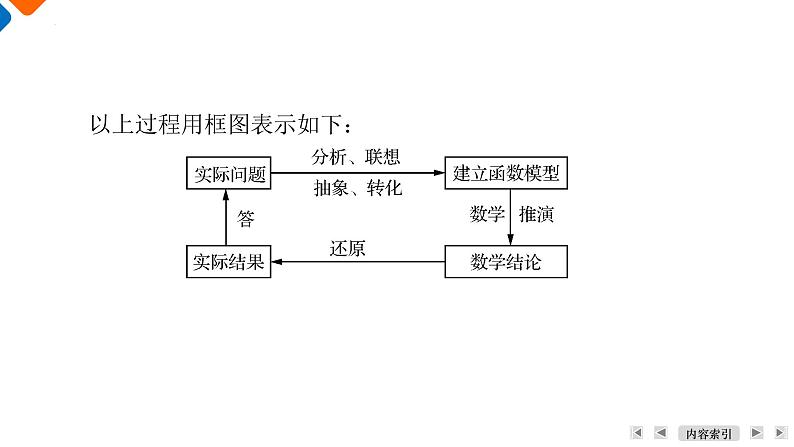
函数应用问题的解题四步骤：(1) 审题：弄清题意，分清条件和结论，理顺数量关系，初步选择函数模型；(2) 建模：将文字语言转化为符号语言，利用数学知识建立相应的函数模型；(3) 解模：求解函数模型，得出数学结论；(4) 还原：将数学结论还原为实际意义的问题．
以上过程用框图表示如下：
1. (2023无锡校联考)“青年兴则国家兴，青年强则国家强”，作为当代青少年，我们要努力奋斗，不断进步．假设我们每天进步1%，则一年后的水平是原来的1.01365≈37.8倍，这说明每天多百分之一的努力，一年后的水平将成倍增长．如果将我们每天的“进步”率从目前的10%提高到20%，要使我们的水平是原来应达水平的1 500倍，那么大约需要(参考数据：lg2≈0.301，lg3≈0.477，lg11≈1.041)(　　)A. 82天 B. 84天C. 86天 D. 88天【分析】 利用对数的运算性质结合估算即可求得结果．
2. (2023南京第五高级中学校考)住房的许多建材都会释放甲醛．甲醛是一种无色、有着刺激性气味的气体，对人体健康有着极大的危害．新房入住时，空气中甲醛浓度不能超过0.08 mg/m3，否则，该新房达不到安全入住的标准．若某套住房自装修完成后，通风x(x＝1,2,3，…，50)周与室内甲醛浓度y(单位：mg/m3)之间近似满足函数关系式y＝0.48－0.1f(x)(x∈N*)，其中f(x)＝lga[k(x2＋2x＋1)](k>0，x＝1,2,3，…，50)，且f(2)＝2，f(8)＝3，则该住房装修完成后要达到安全入住的标准，至少需要通风(　　)A. 17周 B. 24周C. 28周 D. 26周【分析】 由已知数据求得参数a，k，然后解不等式f(x)≥4即可．
【解析】 f(x)＝lga[k(x＋1)2]＝lgak＋2lga(x＋1)，由f(2)＝2，f(8)＝3，得lgak＋2lga3＝2，lgak＋2lga9＝3，两式相减，得lga9＝1，则a＝9，所以lgak＋2＝3，k＝9，该住房装修完成后要达到安全入住的标准，则0.48－0.1f(x)≤0.08，则f(x)≥4，即1＋2lg9(x＋1)≥4，解得x≥26，故至少需要通风26周．
3. 据调查，某自行车存车处在某星期日的存车量为4 000辆次，其中变速车存车费是每辆一次0.3元，普通车存车费是每辆一次0.2元．若普通车存车量为x辆次，存车费总收入为y元，则y关于x的函数关系式是_________________________．
【解析】 由题意，得y＝0.2x＋0.3(4 000－x)＝－0.1x＋1 200，其中0≤x≤4 000.
【答案】 y＝－0.1x＋1 200，x∈[0,4 000]
4. 某种商品进价为4元/件，当日均零售价为6元/件时，日均销售100件，当单价每增加1元，日均销量减少10件，试计算该商品在销售过程中，若每天固定成本为20元，则单价为________元/件时，日利润最大．
【解析】 设单价为(6＋x)元/件，则日均销售量为(100－10x)件，故日利润y＝(6＋x－4)(100－10x)－20＝－10x2＋80x＋180＝－10(x－4)2＋340(0≤x0且a≠1)，则k＝－4，此时y＝－4ax(a>0且a≠1)不满足当x＝2时，y＝8，故不选；若选③y＝klgax(a>0且a≠1)，当x＝0时无意义，故不选．所以选①的函数模型来描述x，y之间的关系．由题意，得当0≤x10p3C. p3＝100p0 D. p1≤100p2
2. (多选)(2023全国高三专题练习)某医药研究机构开发了一种新药，据监测，如果患者每次按规定的剂量注射该药物，注射后每毫升血液中的含药量y(单位：μg)与时间t(单位：h)之间的关系近似满足如图所示的曲线. 据进一步测定，当每毫升血液中含药量不少于0.125 μg时，治疗该病有效，则下列结论中正确的是(　　)
【分析】 利用图象分别求出两段函数解析式，再进行逐个分析，即可解决．
3. (2023全国高三专题练习)折纸是我国民间的一种传统手工艺术，明德小学在课后延时服务中聘请了民间艺术传人给同学们教授折纸. 课堂上，老师给每位同学发了一张长为12 cm，宽为10 cm的矩形纸片，要求大家将纸片沿一条直线折叠．若折痕(线段)将纸片分为面积比为1∶3的两部分，则折痕长度的取值范围是________.【分析】 求出长方形纸片的面积，不妨设折痕将纸片分成两部分的面积分别为S1，S2，则S1＝30cm2，分三种情况，表达出折痕的平方，根据S1＝30cm2得到自变量的取值范围，结合函数的单调性，求出折痕长度的取值范围．
【答案】 [10,13]
【分析】 根据题意，列出分段函数，分段求最值，即可得到结论．
【答案】 200　 10 000