




青岛版八年级上册1.1 全等三角形优秀课件ppt
展开通过实例理解全等图形概念和特征,并能识别图形的全等.
掌握全等三角形的性质,并能应用性质解决简单问题.
掌握全等三角形的相关概念及表示方法.
1.大家分别观察下面的三组图片,若将每一组中的两张图片用适当的方式叠合在一起,它们能够完全重合吗?
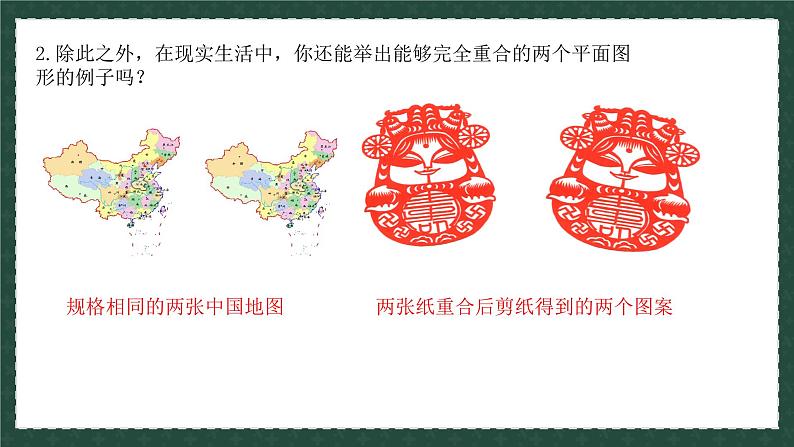
2.除此之外,在现实生活中,你还能举出能够完全重合的两个平面图形的例子吗?
同一张底片洗出的相同尺寸的两张照片
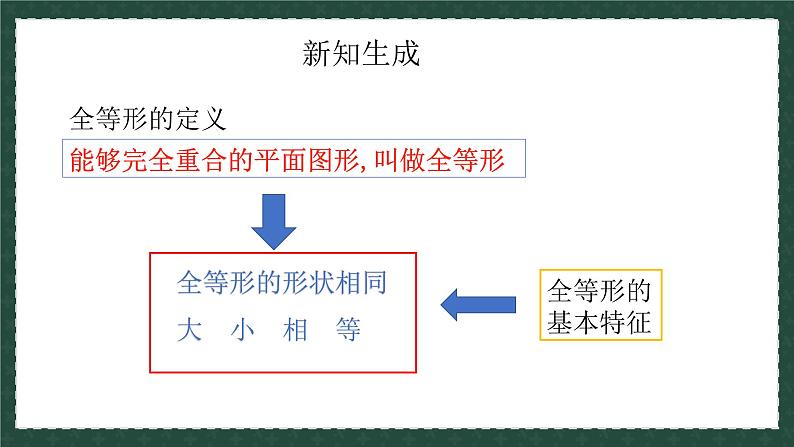
能够完全重合的平面图形,叫做全等形
1.秦兵马俑坑发现于1974年,它被国际上誉为“世界第八大奇迹”.
你能找出图中的兵哪些是全等形吗?
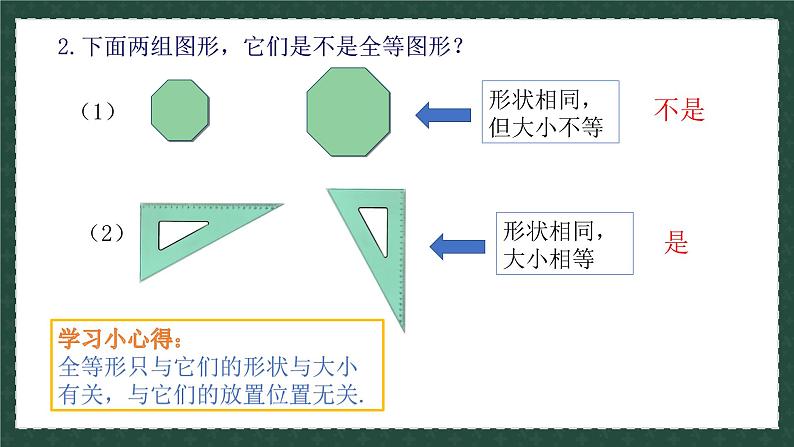
2.下面两组图形,它们是不是全等图形?
学习小心得:全等形只与它们的形状与大小有关,与它们的放置位置无关.
1.用硬纸片任意剪一个三角形,记为△ABC.然后用它做模版,沿它的边缘在纸上画一个三角形,记为△A´B´C´,则△ABC与△A´B´C´是全等形吗?
能够完全重合的两个三角形称为全等三角形
2.当下图中的两个全等三角形完全重合时,你能说出哪些顶点、哪些边、哪些角分别重合吗?
点A与点A´,点B与点B´,点C与点C´
AB与A´B´,AC与A´C´,BC与点B´C´
∠A与∠A´,∠B与∠B´,∠C与∠C´
3.根据这两个全等三角形之间的对应关系,大家思考下列问题
(1)以对应顶点为顶点的角是 对应角吗?举例说明.
(2)以两组对应顶点为端点的 边是对应边吗?举例说明.
(3)对应角所对的边是对应边 吗?举例说明.
(4)对应边所对的角是对应角 吗?举例说明.
对应顶点、对应边、对应角之间的关系规律
(1)以对应顶点为顶点的角是对应角.(2)以两组对应顶点为端点的边是对应边.(3)对应角所对的边是对应边.(4)对应边所对的角是对应角.
4.我们知道“两直线平行”用符号“∥”表示,与此类似,三角形全 等也可以用符号表示.
例如,△ABC与△A´B´C´全等,记作△ABC≌ △A´B´C´,读作△ABC全等于△A´B´C´,符号“≌ ”,读作:“全等于”
在书写两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上,这样可以比较容易地找出全等三角形的对应边与对应角.
(2)这两个三角形的对应角之间有什么关系?
(3)这两个三角形的面积之间有什么关系?
(4)这两个三角形的周长之间有什么关系?
(1)这两个三角形的对应边之间有什么关系?
(2)全等三角形对应角相等
(3)全等三角形面积相等
(4)全等三角形周长相等
例1:如图,△ABC≌△DEF.(1)试找出它们的对应边和对应角.
解:对应边分别是: AB与DE,AC与DF,BC与EF
对应角分别是:∠A与∠D,∠B与∠E,∠ABC与∠DFE
(2)写出这两个三角形中相等的边
解: ∵ΔABC≌ΔDEF ∴AB=DE,AC=DF,BC=EF.
(3)写出图中相等的角.
(4)AB与DE有什么位置关系?
(5)若∠B=60°,∠A=70°,求∠EFD的度数.
∵∠B+∠A+∠ACB=180°
∴∠ACB=180°-∠B-∠A=50°
∴∠EFD=∠ACB=50°
(6)若BF=3cm,求CE的长度.
∴BC-CF=EF-CF
1.已知△ABC 与△DEF全等,其中∠B与∠F是对应角,AB与DF是对应边,写出其它的对应角和对应边.
其它两组对应边为:AC与DE,BC与EF
其它两组对应角为:∠A与∠D,∠C与∠E
2.已知下列图形中的两个三角形全等,请找出它们的对应边与对应角.
对应边为:AB与CD,OB与OD,OA与OC
对应角为:∠AOC与COD,∠A与∠C,∠B与∠D
对应角为:∠C与∠E,∠A与∠D,∠B与∠F
对应边为:AC与ED,CB与EF,AB与DF
对应角为:∠AOB与AOC,∠B与∠C,∠BAO与∠CAO
对应角为:∠BAD与∠CAE,∠B与∠C,∠ADB与∠AEC
对应边为:AD与AE,BD与CE,AB与AC
对应边为:OA与OA,AB与AC,OB与OC
(1) 有公共边的,公共边是对应边(2) 有公共角的,公共角是对应角(3) 有对顶角的,对顶角是对应角(4) 有直角的,直角一定是对应角(5) 两个全等三角形最大边是对应边,最小边也是对应边(6) 两个全等三角形最大角是对应角,最小角也是对应角
运用性质确定法寻找对应元素的常用规律
3.如果△ABC≌△ADE,则与AB相等的边是 ,与∠B相等的角是 ,与∠BAD相等的角是 .
4.已知△ABD≌△CDB (1)∠ABD的对应角是 (2)边AD的对应边是 (3)边AB与边CD的位置关系是 (4)与∠ABC相等的角是
1.已知△ABC≌△DCB.(1)若AB=7cm,CO=5cm,求OD的长度.(2)若∠DBC=80°,∠D=60°,求∠DBO的度数.
2.如图,正方形ABCD沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,NM=5cm,∠DAM=35°求CM的长度与∠BAN的度数.
3.如右图,已知△ABC≌△DFE, 且AC与DE是对应边,若BE=14cm, FC=4cm,求BC的长度.
4.已知Rt△ACB与Rt△DEF全等,,∠C=∠E=90°,AC=4,BC=3.,试求EF的长度.
分两种情况讨论(1)若AC与EF是对应边 ∵Rt△ACB与Rt△DEF全等 ∴EF=AC=4
(2)若AC与DE 是对应边 ∵Rt△ACB与Rt△DEF全等 ∴EF=BC=3
学习小心得:我们在运用全等三角形的性质进行有关计算时,若两个全等三角形的对应关系不能确定,则通常要进行分类讨论.
1.下列说法正确的是( )A.所有的等边三角形都是全等三角形 B.全等三角形是指面积相等的三角形C.周长相等的三角形是全等三角形D.全等三角形是指形状相同大小相等的三角形
3.如图,已知△ABC ≌ △FED,试说明AC∥FD
2.如果△ABC≌△DEF,且△ABC的周长为100 cm,A,B分别与D,E对应, AB=30 cm,DF=25 cm,则BC的长为( ) A.45 cm B.55 cm C.30 cm D. 25 cm
数学七年级上册1.1 我们身边的图形世界课文内容ppt课件: 这是一份数学七年级上册<a href="/sx/tb_c75111_t3/?tag_id=26" target="_blank">1.1 我们身边的图形世界课文内容ppt课件</a>,共21页。PPT课件主要包含了学习目标,你是这样想的吗,议一议,几何体的探究,请你想一想,谁来说一说,几何体的面,体与面的关系等内容,欢迎下载使用。
人教版八年级上册第十二章 全等三角形12.1 全等三角形教学ppt课件: 这是一份人教版八年级上册第十二章 全等三角形12.1 全等三角形教学ppt课件,共20页。PPT课件主要包含了全等三角形,全等三角形的性质,同步练习1,全等于,同步练习2,同步练习3,公共点,公共角,公共边等内容,欢迎下载使用。
数学1.1 全等三角形课前预习课件ppt: 这是一份数学1.1 全等三角形课前预习课件ppt,共23页。PPT课件主要包含了它们会全等吗,翻折旋转,大小都不变,ABC,FDE,EFD,“≌”,读作全等于,几何语言,公共点等内容,欢迎下载使用。














