



九年级上册1.2 怎样判定三角形相似完美版ppt课件
展开学习目标:1.理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用。2.通过应用,培养识图能力和推理论证能力。3.培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值。
重点:理解平行线分线段成比例的事实,并解决实际问题。
难点:探究平行线分线段成比例并简单判定三角形相似。
即对应角相等,对应边的比相等,我们说△ABC与△DEF相似,记作 △ABC∽△DEF,△ABC和△DEF的相似比为k,△DEF与△ABC的相似比为 .
由相似多边形的定义我们知道,在△ABC与△DEF中,如果∠A=∠D, ∠B=∠E, ∠C=∠F,
思考:判定两个三角形相似时,是否存在简便的判定方法呢?
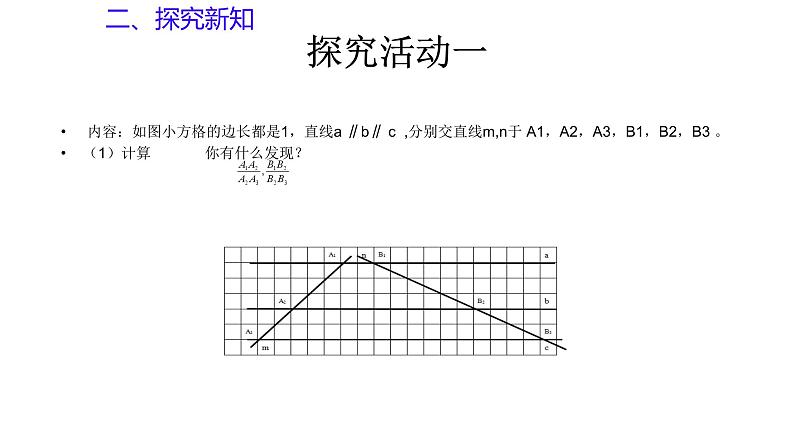
内容:如图小方格的边长都是1,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。 (1)计算 你有什么发现?
(2)将b向下平移到如下图的位置,直线m,n与直线b的交点分别为A2,B2 。你在问题(1)中发现的结论还成立吗?如果将b平移到其他位置呢?
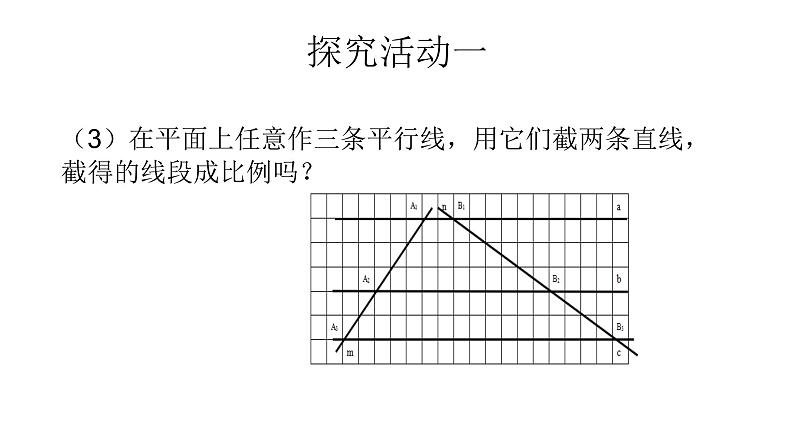
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
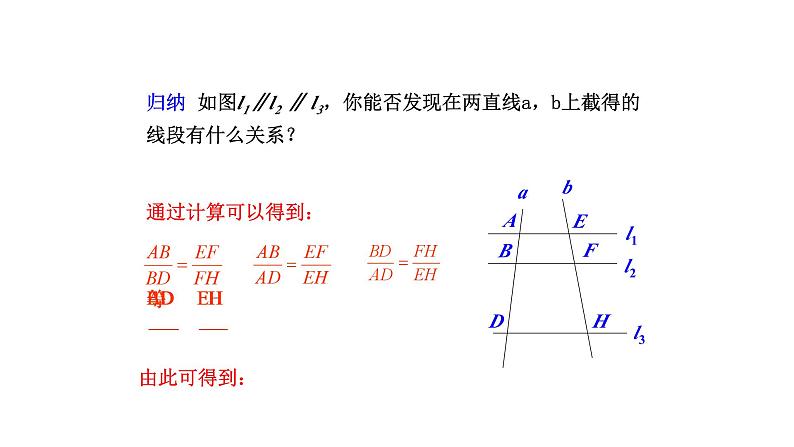
归纳 如图l1∥l2 ∥ l3,你能否发现在两直线a,b上截得的线段有什么关系?
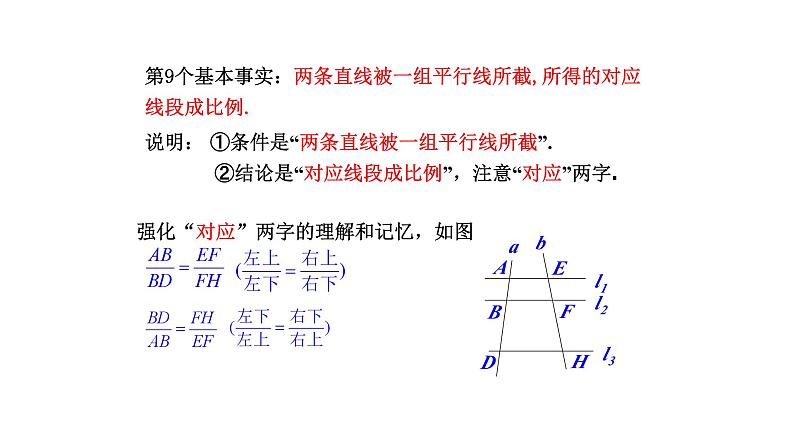
第9个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
说明: ①条件是“两条直线被一组平行线所截”. ②结论是“对应线段成比例”,注意“对应”两字.
强化“对应”两字的理解和记忆,如图
例题1:如图,l1∥l2∥l3,试根据图形写出成比例线段.
例题2:如图3,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。过点A1作直线n的平行线,分别交直线b,c于点C2,C3。(如图4 ),图4中有哪些成比例线段?
如图,DE∥BC,试证明
证明:在△ADE与△ABC中,
过E作EF∥AB交BC于F,
∵四边形DBFE是平行四边形,
平行于三角形一边,并且与其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
拓展:平行于三角形一边的直线与其他两边(或延长线)相交,所得的三角形与原三角形________.
图中共有____对相似三角形.
例题3:已知,如图,AB∥EF∥CD,
△AOB∽△FOE
1、如图,在△ABC中,D、E分别是AB和AC上的点,且 DE∥BC, (1)如果AD = 3.2cm, DB = 1.2cm ,AE=2.4cm,那么EC的长是多少? (2)如果AB = 5cm, AD=3cm,AC = 4cm ,那么EC的长是多少?
2. 如图,A,B两点被池塘隔开,在AB外取一点C,连接AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=38cm,则AB的长为 .
3.如图,在△ABC中,DG∥EH∥FI∥BC,(1)请找出图中所有的相似三角形;(2)如果AD=1,DB=3,那么DG﹕BC=_______.
△ADG∽△AEH∽△AFI∽△ABC
4.如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.
解析:与△ABC相似的三角形有3个:
△ADE △GFC △GOE
5.如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,∠BAC=45°,∠ACB=40°.(1)求∠AED和∠ADE的大小. (2)求DE的长.
由(1)知△ADE∽△ABC,
(1)第9个基本事实:
平行于三角形一边,并且与其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
两条直线被一组平行线所截,所得的对应线段成比例。
平行于三角形一边的直线与其他两边(或延长线)相交,所得的三角形与原三角形相似。
1.必做作业: ①课本P17练习1,2;习题1.1 ——复习与巩固 ②预习1.22.选做作业: 习题1.1 ——复习与巩固第三题
初中数学青岛版(2024)九年级上册3.2 确定圆的条件优秀作业课件ppt: 这是一份初中数学青岛版(2024)九年级上册<a href="/sx/tb_c75359_t3/?tag_id=26" target="_blank">3.2 确定圆的条件优秀作业课件ppt</a>,共23页。PPT课件主要包含了课堂导入,探究新知,课堂练习等内容,欢迎下载使用。
初中数学青岛版(2024)九年级上册3.2 确定圆的条件优秀作业ppt课件: 这是一份初中数学青岛版(2024)九年级上册<a href="/sx/tb_c75359_t3/?tag_id=26" target="_blank">3.2 确定圆的条件优秀作业ppt课件</a>,文件包含32确定圆的条件第1课时分层作业解析版docx、32确定圆的条件第1课时分层作业原卷版docx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
数学2.5 解直角三角形的应用精品课件ppt: 这是一份数学<a href="/sx/tb_c99061_t3/?tag_id=26" target="_blank">2.5 解直角三角形的应用精品课件ppt</a>,共21页。PPT课件主要包含了2边之间的关系,1角之间的关系,两条边或一边一角,温故知新,转化思想,情境导入,能力拔高,课堂小结等内容,欢迎下载使用。














