初中数学湘教版八年级上册2.3 等腰三角形背景图ppt课件

这是一份初中数学湘教版八年级上册2.3 等腰三角形背景图ppt课件，共34页。

知识点1　等腰三角形的性质
1.(新独家原创)如图所示的是一个等腰三角形的风筝,其一 个底角是72°,则顶角的度数是 (　　)A.36°　     B.54°C.36°或54°　    D.54°或72°
解析　∵等腰三角形的底角为72°,∴它的顶角为180°-72°-72°=36°.故选A.
2.(易错题)(2024湖南师大附中植基中学期中)已知等腰三角 形的一个外角为130°,则它的顶角的度数为 (　　)A.50°　     B.80°或50°C.70°或50°　    D.70°或80°
解析　易错点:本题易出现漏解的情况.∵等腰三角形的一个 外角等于130°,∴等腰三角形的一个内角为180°-130°=50°.当50°为顶角时,其他两角为65°、65°;当50°为底角时,其他两角为50°、80°.所以等腰三角形的顶角为50°或80°.故选B.
3.(2024湖南娄底双峰期中)如图,△ABC中,AB=AC,CD⊥AB 于点D,若∠A=40°,则有 (　　) A.∠1=50°　    B.∠1=40°　    C.∠1=35°　    D.∠1=20°
解析　∵CD⊥AB,∴∠ADC=90°,∵AB=AC,∠A=40°,∴∠ ABC=∠ACB=70°,∴∠1=90°-∠ABC=90°-70°=20°.故选D.
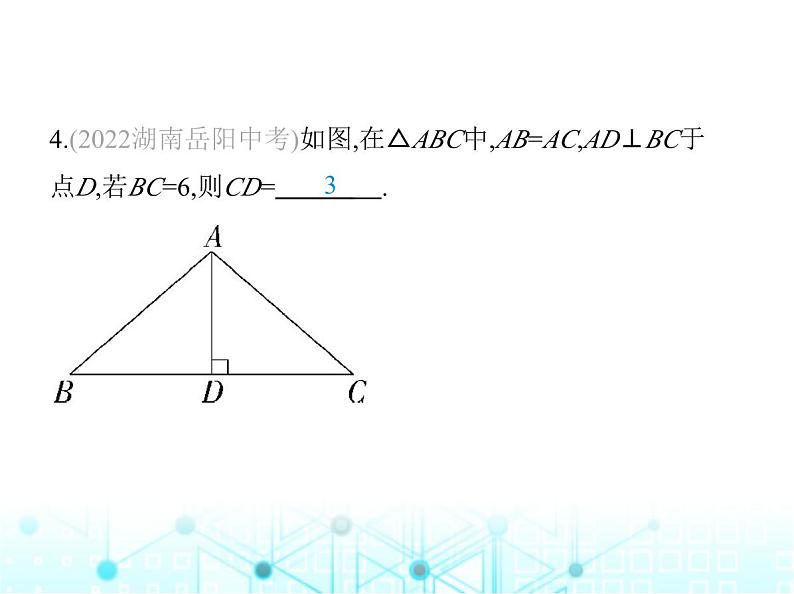
4.(2022湖南岳阳中考)如图,在△ABC中,AB=AC,AD⊥BC于 点D,若BC=6,则CD=　　　    . 
解析　∵AB=AC,AD⊥BC,∴CD=BD,∵BC=6,∴CD=3.
5.如图,在△ABC中,∠B=90°,AB=BD,AD=CD,求∠CAD的度 数.
解析　∵在△ABC中,∠B=90°,AB=BD,∴∠BAD=∠ADB=45°,∵AD=CD,∴∠DCA=∠CAD,∴∠BDA=2∠CAD=45°,∴∠CAD=22.5°.
6.(2023湖南益阳中考)如图,AB∥CD,直线MN与AB,CD分别 交于点E,F,CD上有一点G且GE=GF,∠1=122°,求∠2的度数. 
解析　∵AB∥CD,∴∠MFD=∠1=122°,∵GE=GF,∴∠GFE=∠GEF=180°-∠MFD=180°-122°=58°,∴∠2=180°-58°-58°=64°.
7.如图,在△ABC中,AB=AC,∠BAC和∠ACB的平分线相交于 点D,∠ADC=130°,求∠BAC的度数.
解析　∵AB=AC,AE平分∠BAC,∴AE⊥BC,∴∠AEC=90°,∵∠ADC=130°,∴∠CDE=50°,∴∠DCE=180°-∠AEC-∠CDE=40°,又∵CD平分∠ACB,∴∠ACB=2∠DCE=80°,∵AB=AC,∴∠B=∠ACB=80°,∴∠BAC=180°-(∠B+∠ACB)=20°.
知识点2　等边三角形的性质
8.(2024湖南长沙雅礼教育集团期中)如图,△ABC为等边三角 形,AM∥CN.若∠BAM=25°,则∠BCN= (　　) A.65°　    B.60°　    C.45°　    D.35°
解析　∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,∵AM ∥CN,∴∠MAC+∠ACN=180°,∴∠BAM+∠BAC+∠ACB+∠BCN=180°,即25°+60°+60°+∠BCN=180°,∴∠BCN=35°.故选D.
9.(2022辽宁鞍山中考)如图,直线a∥b,等边三角形ABC的顶 点C在直线b上,∠2=40°,则∠1的度数为 (　　) A.80°　    B.70°　    C.60°　    D.50°
解析　如图,∵△ABC为等边三角形,∴∠A=60°,∵∠A+∠3+ ∠2=180°,∴∠3=180°-40°-60°=80°,∵a∥b,∴∠1=∠3=80°. 故选A. 
10.如图,等边△ABC中,BE和CD分别是AC和AB边上的高,且 相交于点F,则∠BFC的度数为　　　    . 
解析　∵△ABC是等边三角形,∴∠A=60°,∵BE和CD分别是 AC和AB边上的高,∴∠BEC=90°,∠ADC=90°,∴∠ACD=180°-∠A-∠ADC=180°-60°-90°=30°,∴∠BFC=∠BEC+∠ACD=90°+30°=120°.
11.(2024湖南长沙长郡教育集团期中)如图,已知线段AD是等 边△ABC的高,点E在AC上,且AE=AD,则∠ADE=　　　    . 
解析　∵△ABC是等边三角形,AD是等边△ABC的高,∴∠DAC=∠DAB= ∠BAC=30°,∵AE=AD,∴∠ADE=∠AED= = =75°.
12.(2023甘肃白银中考,5,★★☆)如图,BD是等边△ABC的边 AC上的高,以点D为圆心,DB长为半径作弧交BC的延长线于 点E,则∠DEC= (　　)A.20°　    B.25°　    C.30°　    D.35°
解析　在等边△ABC中,∠ABC=60°,∵BD是AC边上的高,∴ BD平分∠ABC,∴∠CBD= ∠ABC=30°,∵BD=ED,∴∠DEC=∠CBD=30°.故选C.
13.(2024山东青岛期末,18,★★☆)如图,等边△ABC中,点D、 E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在点 B'处,DB'、EB'分别交边AC于点F、G.如果测得∠GEC=36°, 那么∠ADF=　　　    . 
解析　∵△ABC为等边三角形,∴∠B=60°,∵∠GEC=36°,∴∠BEG=180°-∠GEC=180°-36°=144°,由翻折的性质得∠BED=∠GED,∠BDE=∠FDE,∴∠BED= ∠BEG= ×144°=72°,∴∠BDE=180°-∠B-∠BED=180°-60°-72°=48°,∴∠BDE=∠FDE=48°,∴∠BDF=∠BDE+∠FDE=96°,
∴∠ADF=180°-∠BDF=180°-96°=84°.
14.(2024湖南邵阳期末,18,★★☆)如图所示,将三个形状、 大小完全一样的等边三角形的一个顶点重合放置,∠BAD=30°,∠GAE=15°,则∠CAF=　　　    . 
解析　∵△ABC,△ADE,△AFG是等边三角形,∴∠BAC=∠DAE=∠FAG=60°,∴∠DAE-∠CAD=∠BAC-∠CAD,∴∠CAE=∠BAD=30°,∴∠CAF=∠FAG-∠CAE-∠GAE=60°-30°-15°=15°.
15.(2024湖南娄底期中,16,★★★)如图,在第1个△A1BC中,∠ B=20°,A1B=CB.在边A1B上任取一点D,延长CA1到点A2,使A1A2 =A1D,连接A2D,得到第2个△A1A2D,在边A2D上任取一点E,延 长A1A2到点A3,使A2A3=A2E,连接A3E,得到第3个△A2A3E,……, 按此方法继续下去,第n个等腰三角形的底角度数是　　     .
解析　∵在△CBA1中,∠B=20°,A1B=CB,∴∠BA1C= =80°,∵A1A2=A1D,∠BA1C是△A1A2D的外角,∴∠DA2A1= ∠BA1C= ×80°;同理∠EA3A2= ×80°,∠FA4A3= ×80°,……∴第n个等腰三角形的底角度数是 ×80°.
16.(2024湖南娄底市直学校期中,24,★★☆)如图,在等腰△ ABC中,AB=AC,点D在BC上,且AD=AE.(1)若∠BAC=90°,∠BAD=30°,求∠EDC的度数.(2)若∠BAC=α(α>30°),∠BAD=30°,求∠EDC的度数.(3)猜想∠EDC与∠BAD的数量关系.(不必证明) 
解析　(1)∵∠BAC=90°,AB=AC,∴∠B=∠C= (180°-∠BAC)=45°,∴∠ADC=∠B+∠BAD=45°+30°=75°,∵∠DAC=∠BAC-∠BAD=90°-30°=60°,AD=AE,∴∠ADE=∠AED= (180°-∠DAC)=60°,∴∠EDC=∠ADC-∠ADE=75°-60°=15°.(2)与(1)类似,由题意得∠B=∠C= (180°-∠BAC)=90°- α,