湘教版八年级上册2.3 等腰三角形课堂教学ppt课件

这是一份湘教版八年级上册2.3 等腰三角形课堂教学ppt课件，共45页。

知识点3　等腰三角形的判定
1.(2024湖南长沙天心月考)在△ABC中,∠A和∠B的度数如 下,能判定△ABC是等腰三角形的是 (　　)A.∠A=30°,∠B=60°　    B.∠A=70°,∠B=50°C.∠A=40°,∠B=70°　    D.∠A=60°,∠B=80°
解析    A.∠C=180°-30°-60°=90°,B.∠C=180°-50°-70°=60°,D.∠C=180°-80°-60°=40°,∴选项A,B,D中的度数不能判定△ABC是等腰三角形;C.∠C=180°-40°-70°=70°=∠B,能判定△ABC是等腰三角形.故选C.
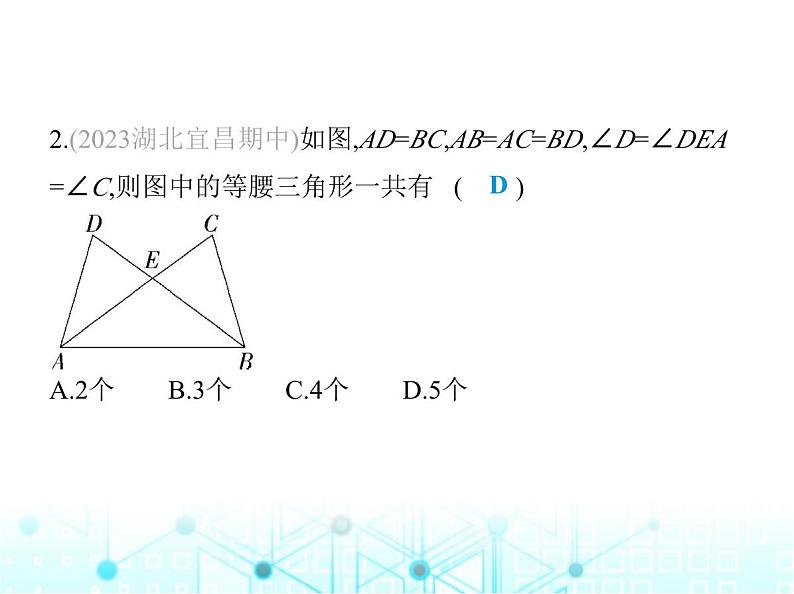
2.(2023湖北宜昌期中)如图,AD=BC,AB=AC=BD,∠D=∠DEA =∠C,则图中的等腰三角形一共有 (　　) A.2个　    B.3个　    C.4个　    D.5个
解析　∵AB=AC=BD,∴△ABD和△ABC是等腰三角形,∵∠D=∠C=∠DEA=∠BEC,∴AD=AE,BC=BE,∴△ADE和△BEC是等腰三角形,∵AD=BC,∴AE=BE,∴△AEB是等腰三 角形,故题图中共有5个等腰三角形.故选D.
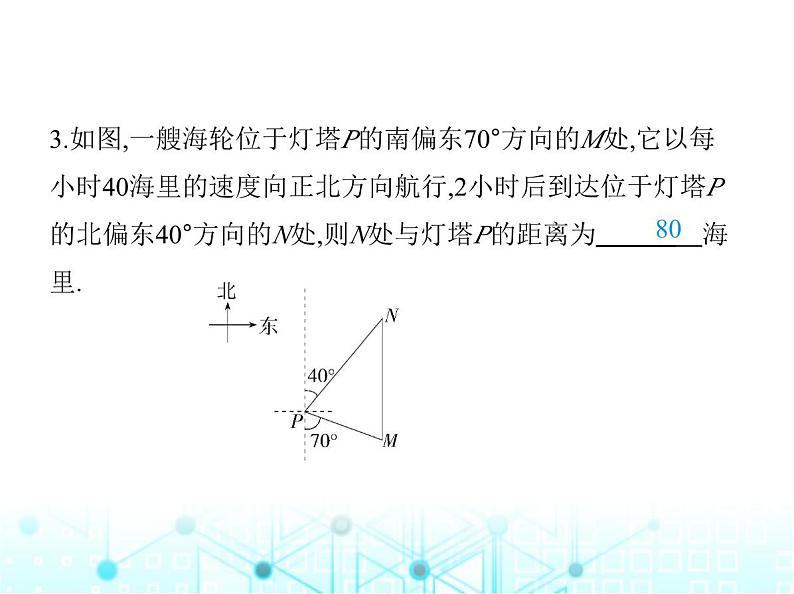
3.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每 小时40海里的速度向正北方向航行,2小时后到达位于灯塔P 的北偏东40°方向的N处,则N处与灯塔P的距离为　　　    海 里. 
解析　如图,∵MN∥PQ,∴∠M=∠APM=70°,∵∠NPM=180°-70°-40°=70°,∴∠NPM=∠M,∴NP=MN=40×2=80(海里),故答案为80. 
4.(新独家原创)如图,将一个长方形ABCD沿着线段BD折叠, 使点C落在点F处,BF与AD相交于E点,若AB=4,BE=5,则重叠 部分的面积是　　　    . 
解析　如图,由折叠可知∠1=∠2,易知∠1=∠3,∴∠2=∠3,∴ED=EB=5,∴重叠部分的面积= DE·AB= ×5×4=10. 
5.(2024湖南永州冷水滩期中)已知:如图,AB=AC,D是AB上一 点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形. 
证明　∵AB=AC,∴∠B=∠C,∵DE⊥BC,∴∠FEB=∠FEC=90°,∴∠B+∠EDB=∠C+∠EFC=90°,∴∠EFC=∠EDB,∵∠EDB=∠ADF,∴∠EFC=∠ADF,∴AD=AF,∴△ADF是等腰三角形.
6.如图,在△ABC中,DE∥AC,EF∥AB,∠BED=∠CEF.(1)试证明△ABC是等腰三角形.(2)探索AB+AC与四边形ADEF周长的关系.
解析　(1)证明:∵DE∥AC,∴∠BED=∠C,∵EF∥AB,∴∠CEF=∠B,∵∠BED=∠CEF,∴∠B=∠C,∴△ABC是等腰三角形.(2)由(1)可得∠C=∠CEF=∠BED=∠B,∴EF=CF,DE=DB,∴AB+AC=AD+BD+CF+AF=AD+DE+EF+ AF=四边形ADEF的周长.
知识点4　等边三角形的判定
7.(2024湖南长沙明德教育集团期中)下列条件中,不能得到 等边三角形的是 (　　)A.有两个内角是60°的三角形B.三边都相等的三角形C.有一个角是60°的等腰三角形D.有两个外角相等的等腰三角形
解析　两个外角相等说明该三角形中有两个内角相等,而等 腰三角形的两个底角是相等的,故不能确定该三角形是等边 三角形.故选D.
8.由于木质衣架没有柔韧性,在挂置衣服的时候不太方便操 作.小明设计了一种衣架,在使用时能轻易收拢,套进衣服后 松开即可.如图,OA=OB=20 cm,当衣架收拢时,∠AOB=60°,此 时A,B两点之间的距离是　　　    cm. 
解析　如图,连接AB.∵OA=OB,∠AOB=60°,∴△OAB是等边三角形,∴AB=OA=20 cm.故答案为20. 
9.如图,在△ABC中,∠ABC=60°,AB=5,若C、B、D三点共线, BE平分∠ABD,AE∥BD,则△ABE的周长是　　　    . 
解析　∵∠ABC=60°,∴∠ABD=180°-60°=120°,∵BE平分∠ABD,∴∠ABE=∠DBE=60°,∵AE∥BD,∴∠EAB=∠ABC=60°,∴∠ABE=∠EAB=60°,∴△ABE是等边三角形,∴AB=BE=AE=5,∴△ABE的周长是AB+BE+AE=15.
10.如图,∠B=∠C,AB∥DE,EC=ED,求证:△DEC为等边三角 形. 
证明　∵∠B=∠C,AB∥DE,∴∠DEC=∠B=∠C,∵EC=ED,∴∠C=∠EDC,∴∠DEC=∠C=∠EDC=60°,∴△DEC为等边三角形.
11.如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD, 求证:△OCD是等边三角形.
证明　∵OA=OB,∴∠B=∠A=60°,∵AB∥CD,∴∠C=∠A=60°,∠D=∠B=60°,∴∠DOC=180°-∠D-∠C=60°,∴△OCD是等边三角形.
12.(2024广西南宁武鸣期中,10,★★☆)如图,在△ABC中,BO, CO分别平分∠ABC和∠ACB,过点O的直线MN∥BC,交AB, AC于点M,N.若MN=6 cm,则BM+CN= (　　) A.6 cm　    B.7 cm　    C.8 cm　    D.9 cm
解析　∵∠ABC、∠ACB的平分线相交于点O,∴∠MBO=∠OBC,∠OCN=∠OCB,∵MN∥BC,∴∠OBC=∠MOB,∠NOC= ∠OCB,∴∠MBO=∠MOB,∠NOC=∠OCN,∴BM=MO,ON= CN,∴BM+CN=MO+ON=MN=6 cm.故选A.
13.(2024湖南郴州永兴期中,9,★★★)如图,AC=DC=3,∠BAC的平分线AD⊥BD于点D,点E为AC的中点,则图中两个 阴影部分面积之差的最大值为 (　　) A.1.5　    B.3　    C.4.5　    D.9
解析　如图,延长BD,AC交于点H.设AD交BE于点O.∵AD⊥ BH,∴∠ADB=∠ADH=90°,∴∠ABD+∠BAD=90°,∠H+∠HAD=90°,∵AD平分∠BAC,∴∠BAD=∠HAD,∴∠ABD=∠H,∴AB=AH,∵AD⊥BH,∴BD=DH,∵DC=CA,∴∠CDA=∠CAD,∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,∴∠CDH=∠H,∴CD=CH=AC,∵E为AC中点,∴AE=EC,
∴S△ABE= S△ABH,S△CDH= S△ABH,∵S△OBD-S△AOE=S△ADB-S△ABE=S△ADH-S△CDH=S△ACD,∵AC=CD=3,∴当DC⊥AC时,△ACD的面积最大,最大面积为 ×3×3=4.5.故选C.
14.(数形结合思想)(2023江西中考,10,★★☆)将含30°角的直 角三角板和直尺按如图所示的方式放置,已知∠α=60°,点B,C 表示的刻度分别为1 cm,3 cm,则线段AB的长为　　　    cm. 
解析　∵直尺的两对边相互平行,∴∠ACB=∠α=60°,∵∠A =60°,∴∠ABC=180°-∠ACB-∠A=180°-60°-60°=60°,∴∠A=∠ABC=∠ACB,∴△ABC是等边三角形,∴AB=BC=3-1=2(cm).
15.(2024湖南常德武陵期中,16,★★★)如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②∠APO=∠DCO;③△OPC是等边 三角形.其中正确的是　　　    .(填序号)
解析　①连接OB(图略),∵AB=AC,AD⊥BC,∴BD=CD,∠BAD= ∠BAC,OB=OC,∵∠BAC=120°,∴∠BAD= ×120°=60°,∴∠ABC=90°-∠BAD=30°,∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°,故①正确;②由①可知,∠APO=∠ABO,∠DCO=∠DBO,∵点O是线段 AD上一点,∴∠ABO与∠DBO不一定相等,∴∠APO与∠DCO不一定相等,故②不正确;
③∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°, ∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,∴∠POC=180°-(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC是等边三角形,故③正确.故答案为①③.
16.(2024湖南湘潭期中,23,★★☆)如图,直线AB∥CD,∠ACD 的平分线CE交AB于点F,∠AFE的平分线交CA的延长线于点 G.(1)求证:AC=AF.(2)若∠FCD=30°,求∠G的大小. 
解析　(1)证明:∵∠ACD的平分线CE交AB于点F,∴∠ACF= ∠DCF,∵AB∥CD,∴∠AFC=∠DCF,∴∠ACF=∠AFC,∴AC=AF.(2)∵∠FCD=30°,AB∥CD,∴∠ACD=∠GAF=60°,∠AFC=30°,∴∠AFE=180°-∠AFC=150°,
∵∠AFE的平分线交CA的延长线于点G,∴∠AFG=∠GFE= ∠AFE= ×150°=75°,∴∠G=180°-∠GAF-∠AFG=180°-60°-75°=45°.
17.(教材变式·P67T7)(2024湖南娄底双峰期中,23,★★☆)学 习几何时,要善于对课本例题中的典型图形进行变式研究.在 △ABC中,AB=BC,∠ABC=60°,BD是AC边上的高,点E为直线 BC上一点,且CE=AD. 
(1)如图1,当点E在边BC上时,求证:△CDE为等边三角形.(2)如图2,当点E在BC的延长线上时,求证:△BDE为等腰三角 形.
证明　(1)∵AB=BC,∠ABC=60°,∴△ABC为等边三角形,∠C=60°,∵BD是AC边上的高,∴AD=CD,∵CE=AD,∴CE=CD,∴△CDE是等边三角形.(2)同(1)可知CD=CE,∴∠CDE=∠E= ∠ACB=30°,∵△ABC为等边三角形,BD是AC边上的高,
∴∠DBC= ∠ABC=30°,∴∠E=∠DBC,∴△BDE为等腰三角形.
18.(新考向·项目式学习试题)(几何直观)在数学实践课上,老 师以“含30°角的直角三角板和等腰三角形纸片”为模具与 同学们开展如下数学活动:在等腰三角形纸片ABC中,CA=CB,∠ACB=120°,将一块含30° 角的足够大的直角三角板PMN(∠M=90°,∠MPN=30°)按如 图所示的方式放置,顶点P在线段AB上滑动(点P不与A,B重 合),三角板的直角边PM始终经过点C,并与CB的夹角为α
(∠PCB=α),斜边PN交AC于点D. 【特例感知】(1)当∠BPC=110°时,α=　　　    ,点P从B向A滑动时,∠ADP 逐渐变　　　    (填“大”或“小”). 【思维拓展】(2)在点P滑动的过程中,△PCD可以是等腰三角形吗?若可 以,请求出α的大小;若不可以,请说明理由.
解析　(1)40°;小.详解:∵CA=CB,∠ACB=120°,∴∠B=30°,∴α=180°-110°-30°=40°.∵∠ADP是△DCP的外角,∴∠ADP=∠ACP+∠MPN,∵在点P从B向A滑动时,α逐渐变大,∠ACP=∠ACB-α,∴∠ACP随着α的变大而逐渐变小,又∵∠MPN=30°,保持不变,
∴∠ADP逐渐变小.(2)△PCD可以是等腰三角形.由题意得∠PCD=120°-α,∠CPD=30°,当△PCD是等腰三角形时,有三种情况:①当PC=PD时,∠PCD=∠PDC= ×(180°-30°)=75°,即120°-α=75°,解得α=45°;②当PD=CD时,∠PCD=∠CPD=30°,即120°-α=30°,解得α=90°;