湘教版八年级上册2.4 线段的垂直平分线背景图课件ppt

这是一份湘教版八年级上册2.4 线段的垂直平分线背景图课件ppt，共29页。
知识点2　线段垂直平分线性质定理的逆定理
1.下列条件中,不能判定直线CD是线段AB(C,D不在线段AB 上)的垂直平分线的是 (　　)A.CA=CB,DA=DB　    B.CA=CB,CD⊥ABC.CA=DA,CB=DB　    D.CA=CB,CD平分AB
解析　当CA=DA,CB=DB时,直线AB是线段CD的垂直平分 线,直线CD不一定是线段AB的垂直平分线.故选C.
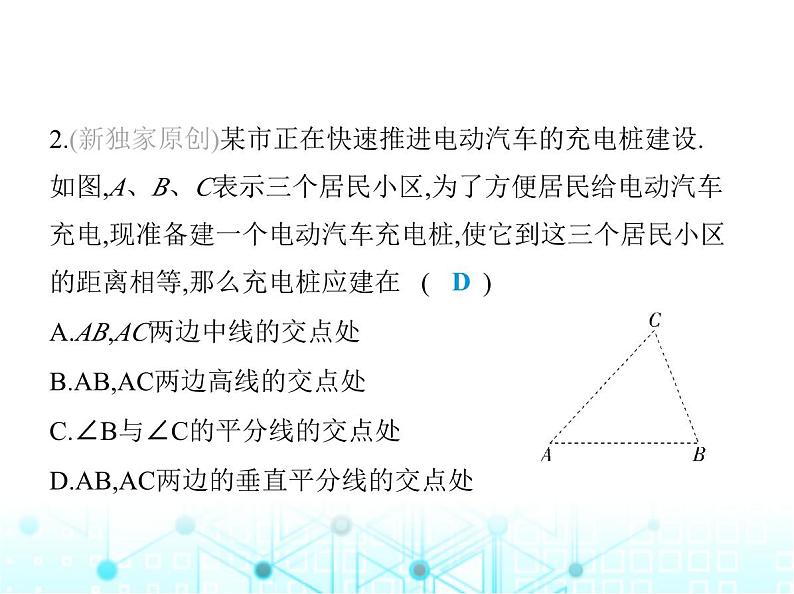
2.(新独家原创)某市正在快速推进电动汽车的充电桩建设. 如图,A、B、C表示三个居民小区,为了方便居民给电动汽车 充电,现准备建一个电动汽车充电桩,使它到这三个居民小区 的距离相等,那么充电桩应建在 (　　)A.AB,AC两边中线的交点处B.AB,AC两边高线的交点处C.∠B与∠C的平分线的交点处D.AB,AC两边的垂直平分线的交点处
解析　∵充电桩到这三个居民小区的距离相等,∴充电桩应 建在△ABC的三边的垂直平分线的交点处.故选D.
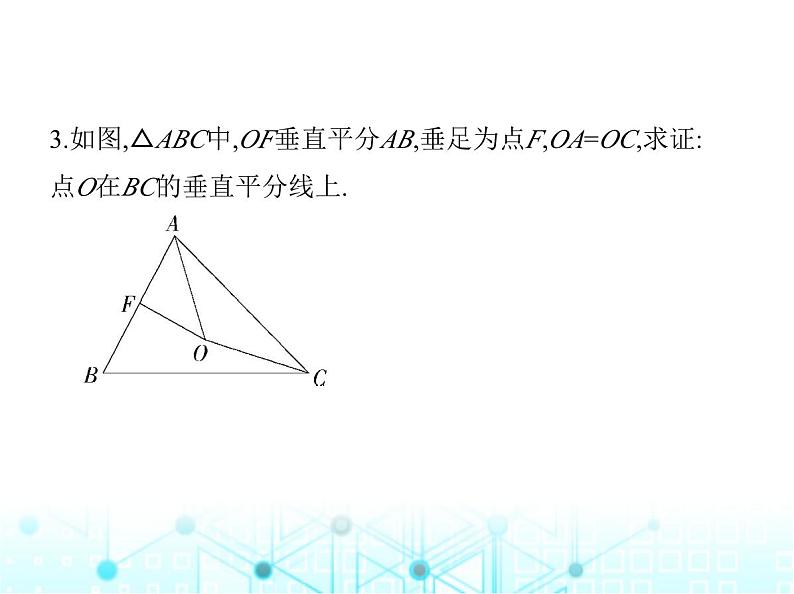
3.如图,△ABC中,OF垂直平分AB,垂足为点F,OA=OC,求证: 点O在BC的垂直平分线上.
证明　连接OB(图略),∵OF垂直平分AB,∴OA=OB,又∵OA=OC,∴OB=OC,∴点O在BC的垂直平分线上.
4.如图,在△ABC中,∠ACB=90°,点P在边AC上,过点P作直线 MN交BC的延长线于点N,交AB于点M,且∠APM=∠A.求证: 点M在线段BN的垂直平分线上.
证明　∵∠ACB=90°,∴∠A+∠B=90°,∠N+∠CPN=90°.∵∠CPN=∠APM,∠APM=∠A,∴∠CPN=∠A,∴∠B=∠N,∴BM=MN,∴点M在线段BN的垂直平分线上.
5.如图,在△ABC中,AB=AC,G为△ABC外一点,且GB=GC.(1)求证:AG垂直平分BC.(2)若点D在AG上,求证:DB=DC.
证明　(1)∵GB=GC,AB=AC,∴点G,点A在线段BC的垂直平分线上,又∵两点确定一条直线,∴AG垂直平分BC.(2)∵AG垂直平分BC,点D在AG上,∴DB=DC.
知识点3　与线段垂直平分线有关的作图
6.如图,在△ABC中,以点A为圆心,AC的长为半径作圆弧交BC 于点D,再分别以点B和点D为圆心,大于 BD的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.若△ADE的 周长为17,AC=7,则AB的长为 (　　)A.4 B.8 C.9 D.10
解析　由作法得AD=AC=7,MN垂直平分BD,∴EB=ED,∵△ADE的周长为17,∴AE+DE+AD=17,∴AE+BE+7=15,即AB+7=17,解得AB=10.故选D.
7.(新考向·尺规作图)(2023海南中考,10,★★☆)如图,在△ ABC中,∠C=40°,分别以点B和点C为圆心,大于 BC的长为半径画弧,两弧相交于M,N两点,作直线MN,交边AC于点D,连接 BD,则∠ADB的度数为 (　　)A.40°B.50° C.80° D.100°
解析　由作图得MN垂直平分BC,∴CD=BD,∴∠CBD=∠C=40°,∴∠ADB=∠C+∠CBD=80°.故选C.
8.(2024湖南衡阳八中教育集团月考,21,★★☆)已知:如图,△ ABC中,EF是AB的垂直平分线,AD⊥BC于点D,且D为CE的中 点.(1)求证:BE=AC.(2)若∠BEF=55°,求∠BAC的度数. 
解析　(1)证明:连接AE(图略),∵EF是AB的垂直平分线,∴AE=BE,∵AD⊥BC,且D为CE的中点,∴AD是CE的垂直平分线,∴AE=AC,∴BE=AC.(2)∵EF⊥AB,∴∠BFE=90°,∵∠BEF=55°,∴∠B=90°-∠BEF=35°,∵EB=EA,∴∠B=∠BAE=35°,∵∠AEC是△ABE的一个外角,
∴∠AEC=∠B+∠BAE=70°,∵AE=AC,∴∠AEC=∠C=70°,∴∠BAC=180°-∠B-∠C=75°.
9.(2024湖南衡阳雁峰期末,23,★★☆)如图,在四边形ABCD 中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.(1)求证:∠BAD=2∠MAN.(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC的度数. 
解析　(1)证明:连接AC,如图. ∵M是CD的中点,AM⊥CD,∴AM是线段CD的垂直平分线,∴AC=AD,又AM⊥CD,∴∠3=∠4,
同理,AB=AC,∠1=∠2,∴∠2+∠3= ∠BAD,即∠BAD=2∠MAN.(2)∵AM⊥CD,AN⊥BC,∠MAN=70°,∴∠BCD=360°-90°-90°-70°=110°,∠BAD=2∠MAN=140°,∴∠BDC=180°-∠DBC-∠BCD=30°,∵AB=AC,AD=AC,∴AB=AD,∴∠ADB=∠ABD=20°,∴∠ADC=∠ADB+∠BDC=50°.
10.(2022湖南怀化溆浦期中,21,★★☆)如图,在△ABC中,∠C =90°,∠A=30°.(1)尺规作图:作AB边的垂直平分线DE,交AC于点D,交AB于 点E(保留作图痕迹,不要求写作法和证明).(2)连接BD,求证:BD平分∠CBA. 
解析　(1)AB边的垂直平分线DE如图所示. (2)证明:如图,∵DE垂直平分AB,∴AD=BD,∴∠ABD=∠A=30°,∵∠C=90°,∴∠ABC=180°-∠C-∠A=60°,
∴∠CBD=∠ABC-∠ABD=60°-30°=30°,∴∠ABD=∠CBD,∴BD平分∠CBA.
11.(推理能力)对于所有的直角三角形,我们都可以将其分割 为两个等腰三角形.例如:如图,已知△ABC中,∠BAC=90°,作直角边AB的垂直平 分线,分别交BC,AB于D,E两点,连接AD,则AD将△ABC分割 成两个等腰三角形:△ADC,△ADB.(1)请将以下证明过程填写完整.
证明:∵DE垂直平分AB,∴AD=DB(　　　　　　　　　　    ),∴∠1=∠2(　　　　　    ),在Rt△ABC中,∠BAC=90°,
∴∠2+∠3=∠BAC=90°,∠1+∠4=180°-∠BAC=90°,∴∠3=∠4,∴CD=DA(　　　　　    ),∴△ADC,△ADB是等腰三角形.(2)根据上述方法,将下面三角形分割成4个等腰三角形.(尺规 作图,保留作图痕迹)
 (3)将下面的不等边三角形分割成5个等腰三角形.(用相同的 字母标出相等的线段)