湘教版八年级上册2.5 全等三角形说课ppt课件

这是一份湘教版八年级上册2.5 全等三角形说课ppt课件，共33页。
知识点8　全等三角形判定方法的灵活运用
1.(2024广西南宁宾阳期中)我国传统工艺中,油纸伞的制作 非常巧妙,其中蕴含着数学知识.如图所示的是油纸伞张开的 示意图,AE=AF,GE=GF,则△AEG≌△AFG的依据是(      )
A.SAS　    B.ASA　    C.AAS　    D.SSS
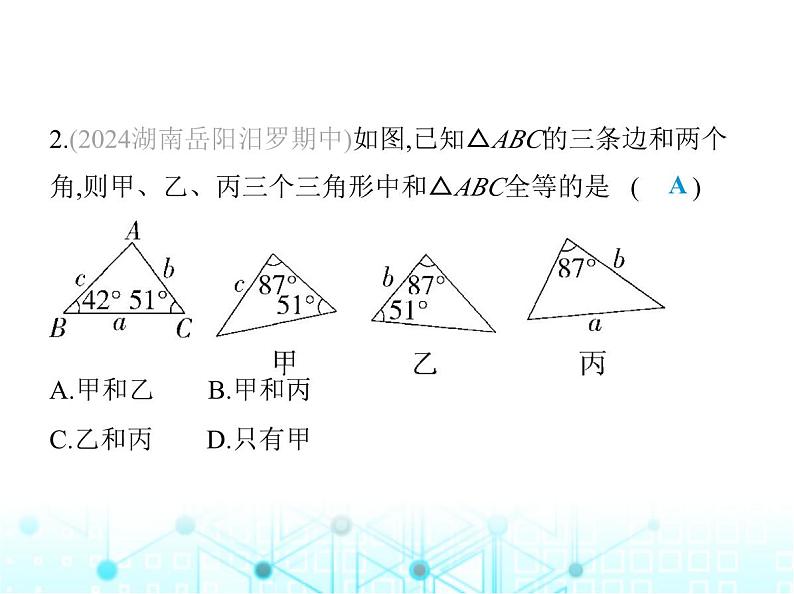
2.(2024湖南岳阳汨罗期中)如图,已知△ABC的三条边和两个 角,则甲、乙、丙三个三角形中和△ABC全等的是 (　　) A.甲和乙　    B.甲和丙　    C.乙和丙　    D.只有甲
解析　∠A=180°-42°-51°=87°,根据AAS可以判定甲与△ABC全等,根据ASA可以判定乙与△ABC全等.故选A.
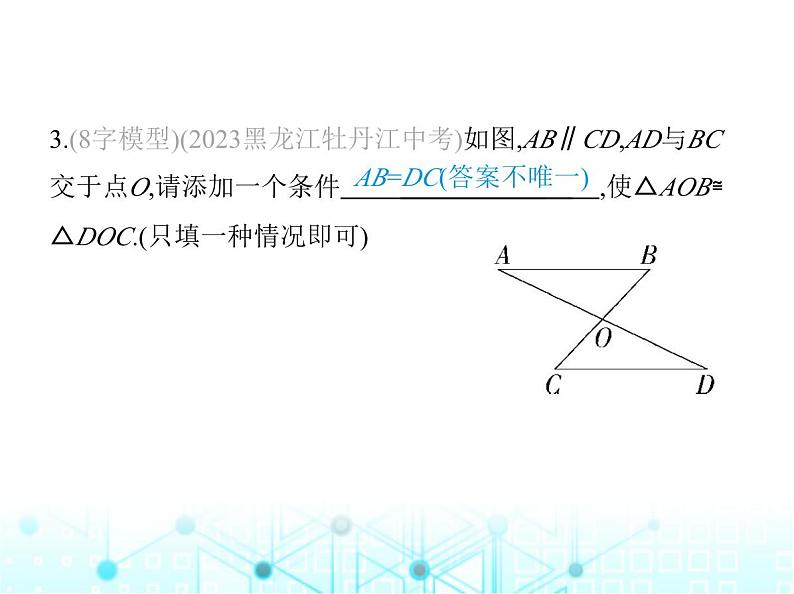
3.(8字模型)(2023黑龙江牡丹江中考)如图,AB∥CD,AD与BC 交于点O,请添加一个条件　 　 　    ,使△AOB≌△DOC.(只填一种情况即可)   
AB=DC(答案不唯一)
解析　∵AB∥CD,∴∠A=∠D,∠B=∠C,∴添加条件AB=DC, 由ASA可证明△AOB≌△DOC.答案不唯一.
4.(2023浙江衢州中考)已知:如图,在△ABC和△DEF 中,B,E,C,F在同一条直线上.下面有四个条件:①AB=DE;②AC=DF;③BE=CF;④∠ABC=∠DEF.(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情 况即可).(2)在(1)的条件下,求证:△ABC≌△DEF. 
解析　(1)由题意知,选择的三个条件是①②③或①③④,选 择一种即可.(2)当选择①②③时,证明:∵BE=CF,∴BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中, ∴△ABC≌△DEF(SSS).当选择①③④时,
证明:∵BE=CF,∴BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中, ∴△ABC≌△DEF(SAS).
5.(2024广西南宁期中)如图,点D,E在△ABC的边BC上,连接 AD,AE,若AB=AC,AD=AE,试证明:BD=CE.圆圆的证明过程如下: 证明:∵AB=AC,∴∠B=∠C,在△ABD与△ACE中,
 ∴△ABD≌△ACE,∴BD=CE.她的证明过程　　　    (填“正确”或“错误”).若错误,请 写出正确的证明过程.
解析　利用SSA,不能判定△ABD≌△ACE,∴圆圆的证明过 程是错误的.正确的证明过程如下:证明:∵AB=AC,AD=AE,∴∠B=∠C,∠ADE=∠AED,∴∠ADB=∠AEC,在△ABD与△ACE中, ∴△ABD≌△ACE(AAS),∴BD=CE.
6.如图,已知点D、E是△ABC内两点,且∠BAE=∠CAD,AB= AC,AD=AE,连接BD,CE.(1)求证:△ABD≌△ACE.(2)延长BD,CE交于点F,若∠BAC=86°,∠ABD=20°,求∠BFC 的度数.
解析　(1)证明:∵∠BAE=∠CAD,∴∠BAE-∠DAE=∠CAD- ∠DAE,即∠BAD=∠CAE,在△ABD和△ACE中, ∴△ABD≌△ACE(SAS).(2)∵△ABD≌△ACE,∴∠ACE=∠ABD=20°,又∵∠BAC=86°,∴∠FBC+∠FCB=180°-86°-20°-20°=54°,
∴∠BFC=180°-54°=126°.
7.(2024湖南邵阳武冈期中,10,★★☆)两组邻边分别相等的 四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中 AD=CD,AB=CB,AC,BD交于点O.小明在探究筝形的性质时, 得到如下结论:①AC⊥BD;②AO=CO= AC;③△ABD≌△CBD;④四边形ABCD的面积=AC·BD.其中正确的结论有 (　　)
A.1个　    B.2个　    C.3个　    D.4个
解析　在△ABD与△CBD中, ∴△ABD≌△CBD(SSS),∠ADB=∠CDB,∴③正确.在△AOD与△COD中,  ∴△AOD≌△COD(SAS),∴∠AOD=∠COD= ×180°=90°,AO=CO= AC,∴AC⊥BD,①②正确.四边形ABCD的面积=S△ADB+S△BDC= DB·OA+ DB·OC= BD·AC,故
8.(2024河南南阳期中,9,★★☆)小丽与爸妈在公园里荡秋 千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚 在地面上用力一蹬,妈妈在距地面1 m高的B处接住她后用力 一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离 BD、CE的长分别为1.4 m和1.8 m,∠BOC=90°,则爸爸在C处 接住小丽时,小丽距离地面的高度是 (　　)
 A.1 m　    B.1.6 mC.1.8 m　    D.1.4 m
解析　由题意可知∠CEO=∠BDO=90°,OB=OC,∵∠BOC=∠BDO=90°,∴∠COE+∠BOD=∠BOD+∠OBD= 90°,∴∠COE=∠OBD,在△COE和△OBD中, ∴△COE≌△OBD(AAS),∴CE=OD,OE=BD,∵BD、CE的长分别为1.4 m和1.8 m,∴DE=OD-OE=CE-BD=1.8-1.4=0.4(m),
∵B处距地面1 m高,∴DF=1 m,∴EF=DF+DE=1.4 m,即爸爸在C处接住小丽时, 小丽距离地面的高度是1.4 m.故选D.
9.(一题多解)(截长补短法)(2024贵州遵义月考,23,★★☆)如 图,在△ABC中,AB>AC,点D在BC上,∠1=∠2,P为AD上任意 一点,连接BP、CP,求证:AB-AC>PB-PC. 
证明　证法一(截长法):如图,在AB上截取AE,使AE=AC,连接 PE, 在△AEP和△ACP中, 
∴△AEP≌△ACP(SAS),∴PE=PC,在△PBE中,BE>PB-PE,即AB-AC>PB-PC.证法二(补短法):如图,延长AC到点E,使AE=AB,连接PE,
在△AEP和△ABP中, ∴△AEP≌△ABP(SAS),∴PE=PB,在△PCE中,CE>PE-PC,即AB-AC>PB-PC.
10.(2024湖南株洲渌口期中)如图,在等腰Rt△ACB中,∠ACB =90°,AC=BC,E点为射线CB上一动点,连接AE,过点A作AF⊥ AE且AF=AE.(1)如图1,过F点作FG⊥AC,交AC于G点,求证:△AGF≌△E-CA.(2)如图2,连接BF,交AC于D点,若 =3,求证:E点为BC中点.(3)如图3,当E点在线段CB的延长线上时,连接BF,与AC的延 长线交于D点,若 = ,则 =　　　    .
解析　(1)证明:∵AF⊥AE,FG⊥AC,∴∠FAE=∠FGA=90°,∴∠FAG+∠CAE=90°,∠FAG+∠F=90°,∴∠CAE=∠F,在△AGF和△ECA中, ∴△AGF≌△ECA(AAS).(2)证明:如图,过F点作FM⊥AC交AC于M点,
 由(1)易知△AMF≌△ECA,∴FM=AC=BC,AM=CE,∵FM⊥AC,∴∠FMD=90°,在△FMD和△BCD中, ∴△FMD≌△BCD(AAS),∴DM=CD,
∵ =3,∴ =2,∴ = .∵AM=CE,AC=BC,∴ = ,∴E点为BC中点.(3)如图,过点F作FN⊥AD,交AD的延长线于点N,由(1)(2)易知△ANF≌△ECA,△DNF≌△DCB,