



还剩11页未读,
继续阅读
所属成套资源:青岛版2024-2025八年级上册数学同步课堂课件+练习
成套系列资料,整套一键下载
初中数学青岛版八年级上册1.2 怎样判定三角形全等获奖ppt课件
展开
这是一份初中数学青岛版八年级上册1.2 怎样判定三角形全等获奖ppt课件,共19页。PPT课件主要包含了第一章全等三角形,第一课时,学习目标,实验与探究,提出问题,探究问题,1一条边相等,2一个角相等,不能保证全等,1两边相等等内容,欢迎下载使用。
1.2 全 等 三 角 形
经历探索三角形全等条件的过程,体会分析问题的方法,积累数学活动的经验.
掌握三角形全等的“边角边”的条件.
会利用“边角边”判别两个三角形全等,解决一些简单的实际问题.
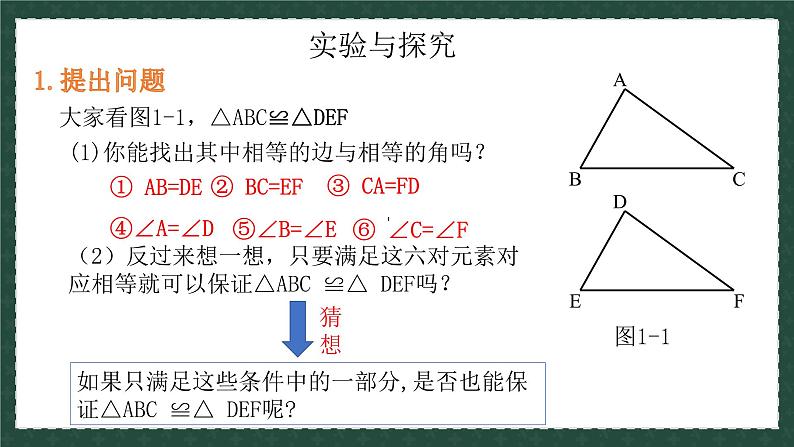
大家看图1-1,△ABC≌△DEF
(1)你能找出其中相等的边与相等的角吗?
(2)反过来想一想,只要满足这六对元素对应相等就可以保证△ABC ≌△ DEF吗?
如果只满足这些条件中的一部分,是否也能保证△ABC ≌△ DEF呢?
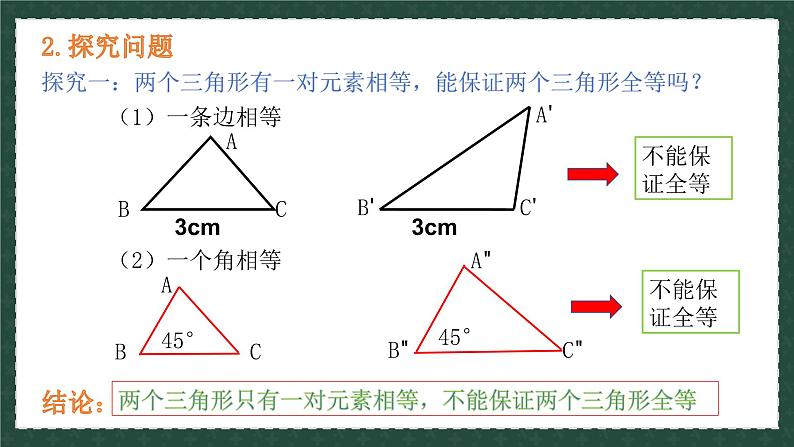
探究一:两个三角形有一对元素相等,能保证两个三角形全等吗?
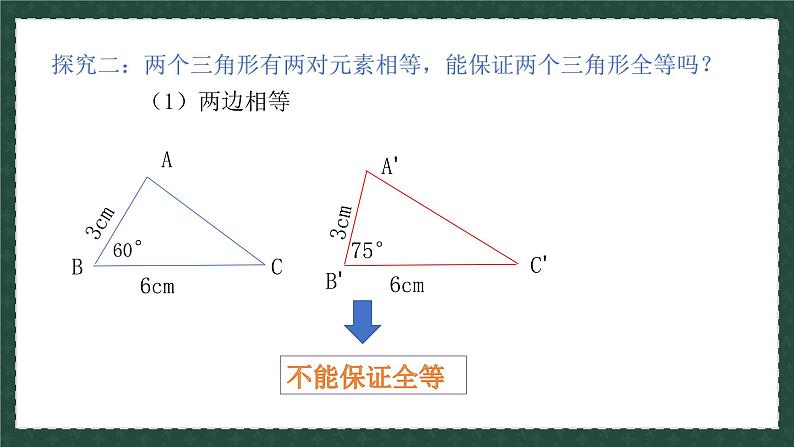
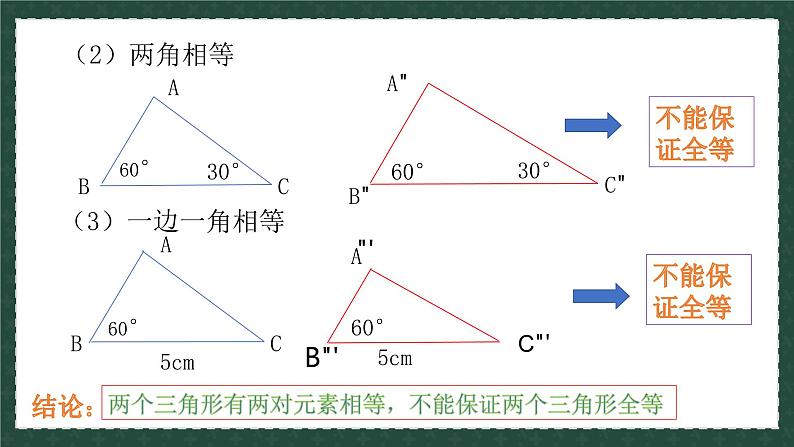
探究二:两个三角形有两对元素相等,能保证两个三角形全等吗?
想一想:如果两个三角形满足三对元素对应相等,则你能说出有哪几种可能情况吗?
探究三 :两边一角分别相等两个三角形全等吗?
两边和它们的夹角对应相等的两个三角形全等
简写成“边角边”或“SAS”
在△ABC和△DEF中, AB=DE ∠B=∠E BC=EF∴ △ABC≌△DEF (SAS)
(1)在△ABC与△ABF中,满足了哪些元素对应相等?
AB=AB,∠B=∠B,AC=AF
(2)∠B与∠B是两组等边的夹角吗?
(3)这两个三角形全等吗?
两边及其中一边所对的角对应相等的两个三角形不一定全等.
∠B与∠B分别是一组等边的对角
温馨提示:我们在运用SAS判定两个三角形全等时,相等的角一定是两组等边的夹角.
例1 已知如图,AB=AD,∠BAC=∠DAC,△ABC与△ADC全等吗?试说明理由.
解:△ABC与△ADC全等. 理由如下:
在△ABC与△ADC中,
∴ △ABC≌△ADC(SAS)
例2 为了测量池塘边上不能直接到达的两点A,B之间的距离,小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离.他的方案对吗?请你说明理由.
解:他的方案对. 理由如下:
学习小心得我们判定两个三角形全等时,一定要注意观察图中有没有对顶角,对顶角一定相等.
1.如图,已知AD=BC,∠DAB=∠CBA,△ABD与△BAC全等吗?
2.已知,AB=AD,AC=AE,∠CBE和∠EDC相等吗?为什么?
学习小心得我们判定两个三角形全等时,一定要留心观察图中有没有公共角,公共角一定相等.
3.如图,已知点E,F在SC上,∠1=∠2,AF=AE,BA=CA,△AFB与△AEC是否全等?
4.如图,E,F在BC上,BE=CF,AB=CD,∠B=∠C,AB与CD有怎样的位置关系?
1.如图,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE,连接BD、CE,得到△ABD与△ACE,则这两个三角形全等吗?
2.如图,AD是△ABC的中线,AB=8,AC=6,求AD的取值范围.
解:延长AD至点E,使DE=AD, 连接CE.
∵AD为中线∴BD=CD
1.如图,已知∠CAB=∠DAB,要使△ABC≌△ABD,可添加的一个条件是
2. 如图,AC和BD相交于点O,OA=OC,OB=OD则DC与AB的位置关系是什么?
3.已知∠ACB=∠CDE=90°,AC=CD,CB=DE,则AB与CE的位置关系如何?
1.2 全 等 三 角 形
经历探索三角形全等条件的过程,体会分析问题的方法,积累数学活动的经验.
掌握三角形全等的“边角边”的条件.
会利用“边角边”判别两个三角形全等,解决一些简单的实际问题.
大家看图1-1,△ABC≌△DEF
(1)你能找出其中相等的边与相等的角吗?
(2)反过来想一想,只要满足这六对元素对应相等就可以保证△ABC ≌△ DEF吗?
如果只满足这些条件中的一部分,是否也能保证△ABC ≌△ DEF呢?
探究一:两个三角形有一对元素相等,能保证两个三角形全等吗?
探究二:两个三角形有两对元素相等,能保证两个三角形全等吗?
想一想:如果两个三角形满足三对元素对应相等,则你能说出有哪几种可能情况吗?
探究三 :两边一角分别相等两个三角形全等吗?
两边和它们的夹角对应相等的两个三角形全等
简写成“边角边”或“SAS”
在△ABC和△DEF中, AB=DE ∠B=∠E BC=EF∴ △ABC≌△DEF (SAS)
(1)在△ABC与△ABF中,满足了哪些元素对应相等?
AB=AB,∠B=∠B,AC=AF
(2)∠B与∠B是两组等边的夹角吗?
(3)这两个三角形全等吗?
两边及其中一边所对的角对应相等的两个三角形不一定全等.
∠B与∠B分别是一组等边的对角
温馨提示:我们在运用SAS判定两个三角形全等时,相等的角一定是两组等边的夹角.
例1 已知如图,AB=AD,∠BAC=∠DAC,△ABC与△ADC全等吗?试说明理由.
解:△ABC与△ADC全等. 理由如下:
在△ABC与△ADC中,
∴ △ABC≌△ADC(SAS)
例2 为了测量池塘边上不能直接到达的两点A,B之间的距离,小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离.他的方案对吗?请你说明理由.
解:他的方案对. 理由如下:
学习小心得我们判定两个三角形全等时,一定要注意观察图中有没有对顶角,对顶角一定相等.
1.如图,已知AD=BC,∠DAB=∠CBA,△ABD与△BAC全等吗?
2.已知,AB=AD,AC=AE,∠CBE和∠EDC相等吗?为什么?
学习小心得我们判定两个三角形全等时,一定要留心观察图中有没有公共角,公共角一定相等.
3.如图,已知点E,F在SC上,∠1=∠2,AF=AE,BA=CA,△AFB与△AEC是否全等?
4.如图,E,F在BC上,BE=CF,AB=CD,∠B=∠C,AB与CD有怎样的位置关系?
1.如图,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE,连接BD、CE,得到△ABD与△ACE,则这两个三角形全等吗?
2.如图,AD是△ABC的中线,AB=8,AC=6,求AD的取值范围.
解:延长AD至点E,使DE=AD, 连接CE.
∵AD为中线∴BD=CD
1.如图,已知∠CAB=∠DAB,要使△ABC≌△ABD,可添加的一个条件是
2. 如图,AC和BD相交于点O,OA=OC,OB=OD则DC与AB的位置关系是什么?
3.已知∠ACB=∠CDE=90°,AC=CD,CB=DE,则AB与CE的位置关系如何?














