





高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.5 函数的应用(二)4.5.3 函数模型的应用教学演示ppt课件
展开[学习目标] 1.会利用已知函数模型解决实际问题.(数学运算)2.能建立函数模型解决实际问题.(数学建模)3.了解拟合函数模型并解决实际问题.(数据分析)[讨论交流] 预习教材P148-P154,并思考以下问题:问题1.应用指数型函数模型、对数型函数模型解决实际问题时应注意些什么?问题2.建立函数模型解决实际问题的流程是什么?
[自我感知] 经过认真的预习,结合对本节课的理解和认识,请画出本节课的知识逻辑体系.
探究1 应用已知函数模型解决实际问题
【链接·教材例题】例3 人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为制定一系列相关政策提供依据.早在1798年,英国经济学家马尔萨斯(,1766-1834)就提出了自然状态下的人口增长模型y=y0ert,
其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的增长率,r是常数 .(1)根据国家统计局网站公布的数据,我国1950年末、1959年末的人口总数分别为55 196万和67 207万.根据这些数据,用马尔萨斯人口增长模型建立我国在1950~1959年期间的具体人口增长模型.(2)利用(1)中的模型计算1951~1958年各年末的人口总数.查阅国家统计局网站公布的我国在1951~1958年间各年末的实际人口总数,检验所得模型与实际人口数据是否相符.(3)以(1)中的模型作预测,大约在什么时候我国人口总数达到13亿?
分析:用马尔萨斯人口增长模型建立具体人口增长模型,就是要确定其中的初始量y0和增长率r.
解:(1)由题意可设1950年为t=0,则y0=55 196,根据马尔萨斯人口增长模型,有67 207=55 196e9r,由计算工具得r≈0.021 876.因此,用马尔萨斯人口增长模型建立的我国在1950~1959年期间的人口增长模型为y=55 196e0.021 876t,t∈[0,9].
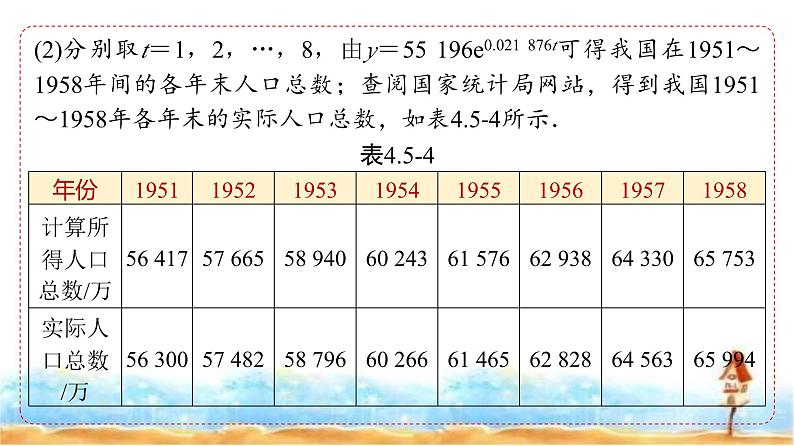
(2)分别取t=1,2,…,8,由y=55 196e0.021 876t可得我国在1951~1958年间的各年末人口总数;查阅国家统计局网站,得到我国1951~1958年各年末的实际人口总数,如表4.5-4所示.表4.5-4
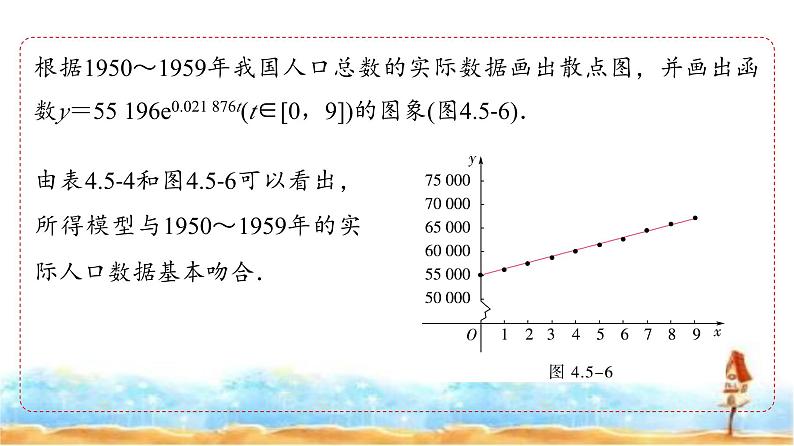
根据1950~1959年我国人口总数的实际数据画出散点图,并画出函数y=55 196e0.021 876t(t∈[0,9])的图象(图4.5-6).
由表4.5-4和图4.5-6可以看出,所得模型与1950~1959年的实际人口数据基本吻合.
(3)将y=130 000代入y=55 196e0.021 876t,由计算工具得t≈39.16.所以,如果人口按照(1)中的模型增长,那么大约在1950年后的第40年(即1990年),我国的人口就已达到13亿.
[典例讲评] 1.著名数学家、物理学家牛顿曾提出:物体在空气中冷却,如果物体的初始温度为θ1 ℃,空气温度为θ0 ℃,则t分钟后物体的温度θ(单位:℃)满足:θ=θ0+(θ1-θ0)e-kt.若常数k=0.05,空气温度为30 ℃,某物体的温度从110 ℃下降到40 ℃,大约需要的时间为( )(参考数据:ln 2≈0.69)A.39分钟 B.41分钟 C.43分钟 D.45分钟
反思领悟 已知函数模型解决实际问题,往往给出的函数解析式含有参数,需要将题中的数据代入函数模型,求得函数模型中的参数,再将问题转化为已知函数解析式求函数值或自变量的值.
探究2 自建确定性函数模型解决实际问题
【链接·教材例题】例4 2010年,考古学家对良渚古城水利系统中一条水坝的建筑材料(草裹泥)上提取的草茎遗存进行碳14年代学检测,检测出碳14的残留量约为初始量的55.2%,能否以此推断此水坝大概是什么年代建成的?
分析:因为死亡生物机体内碳14的初始量按确定的衰减率衰减,属于指数衰减,所以应选择函数y=kax(k∈R,且k≠0;a>0,且a≠1)建立数学模型.
例5 假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多回报10元;方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.请问,你会选择哪种投资方案?
分析:我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据.
解:设第x天所得回报是y元,则方案一可以用函数y=40(x∈N*)进行描述;方案二可以用函数y=10x(x∈N*)进行描述;方案三可以用函数y=0.4×2x-1(x∈N*)进行描述.三个模型中,第一个是常数函数,后两个都是增函数.要对三个方案作出选择,就要对它们的增长情况进行分析.我们先用信息技术计算一下三种方案所得回报的增长情况(表4.5-5).
再画出三个函数的图象(图4.5-7).
由表4.5-5和图4.5-7可知,方案一的函数是常数函数,方案二、方案三的函数都是增函数,但方案三的函数与方案二的函数的增长情况很不相同.可以看到,尽管方案一、方案二在第1天所得回报分别是方案三的100倍和25倍,但它们的增长量固定不变,而方案三是“指数增长”,其“增长量”是成培增加的,从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一、方案二所无法企及的.从每天所得回报看,在第1~3天,方案一最多;在第4天,方案一和方案二一样多,方案三最少;在第5~8天,方案二最多;第9天开始,方案三比其他两个方案所得回报多得多,到第30天,所得回报已超过2亿元.
下面再看累计的回报数.通过信息技术列表如下(表4.5-6).表4.5-6
因此,投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8~10天,应选择方案二;投资11天(含11天)以上,则应选择方案三.
反思领悟 在实际问题中,有关人口增长、银行复利、细胞分裂等增长率问题常可以用指数型函数模型表示,通常可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x为时间)的形式.
[学以致用] 2.据观测统计,某湿地公园某种珍稀鸟类的现有个数约为1 000,并以平均每年8%的速度增加.(1)求两年后这种珍稀鸟类的大约个数;(2)写出y(珍稀鸟类的个数)关于x(经过的年数)的函数关系式;(3)约经过多少年以后,这种鸟类的个数达到现有个数的3倍或以上?(结果为整数)(参考数据:lg 2≈0.301 0,lg 3≈0.477 1)
[解] (1)依题意,一年后这种鸟类的个数为1 000+1 000×8%=1 080,两年后这种鸟类的个数为1 080+1 080×8%≈1 166.(2)由题意可知珍稀鸟类的现有个数约为1 000,并以平均每年8%的速度增加,则所求的函数关系式为y=1 000×1.08x,x∈N.
探究3 拟合数据构建函数模型解决实际问题
【链接·教材例题】例6 某公司为了实现1 000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:y=0.25x,y=lg7x+1,y=1.002x,其中哪个模型能符合公司的要求?
分析:本例提供了三个不同增长方式的奖励模型,按要求选择其中一个函数作为刻画奖金总数与销售利润的关系.由于公司总的利润目标为1 000万元,所以销售人员的销售利润一般不会超过公司总的利润.于是,只需在区间[10,1 000]上,寻找并验证所选函数是否满足两条要求:第一,奖金总数不超过5万元,即最大值不大于5;第二,奖金不超过利润的25%,即y≤0.25x.不妨先画出函数图象,通过观察函数图象,得到初步的结论,再通过具体计算,确认结果.
解:借用信息技术画出函数y=5,y=0.25x,y=lg7x+1,y=1.002x的图象(图4.5-8).观察图象发现,在区间[10,1 000]上,模型y=0.25x,y=1.002x的图象都有一部分在直线y=5的上方,只有模型y=lg7x+1的图象始终在y=5的下方,这说明只有按模型y=lg7x+1进行奖励时才符合公司的要求.
对于模型y=lg7x+1,它在区间[10,1 000]上单调递增,而且当x=1 000时,y=lg71 000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.再计算按模型y=lg7x+1奖励时,奖金是否不超过利润的25%,即当x∈[10,1 000]时,是否有y≤0.25x,即lg7x+1≤0.25x成立.令f (x)=lg7x+1-0.25x,x∈[10,1 000],利用信息技术画出它的图象(图4.5-9).
由图象可知函数f (x)在区间[10,1 000]上单调递减,因此f (x)≤f (10)≈-0.316 7<0,即lg7x+1<0.25x.所以,当x∈[10,1 000]时,y≤0.25x,说明按模型y=lg7x+1奖励,奖金不会超过利润的25%.综上所述,模型y=lg7x+1确实能符合公司要求.
[典例讲评] 3.某科研小组对面积为8 000平方米的某池塘里的一种生物的生长规律进行研究,一开始在此池塘投放了一定面积的该生物,观察试验得到该生物覆盖面积y(单位:平方米)与所经过月数x(x∈N)的下列数据:
反思领悟 函数拟合与预测的一般步骤(1)根据原始数据、表格,绘出散点图.(2)通过观察散点图,画出拟合直线或拟合曲线.(3)求出拟合直线或拟合曲线的函数关系式.(4)利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.
[学以致用] 3.数据显示,某新创业的IT公司2023年上半年五个月的收入情况如表所示:
【教用·备选题】 在密闭培养环境中,某类细菌的繁殖速度在初期会较快,随着单位体积内细菌数量的增加,繁殖速度又会减慢.在一次实验中,检测到这类细菌在培养皿中的数量y(单位:百万个)与培养时间x(单位:小时)的关系为:
根据表格中的数据画出散点图如下:
1.某研究小组在一项试验中获得一组关于y,t的数据,将其整理得到如图所示的散点图.下列函数中,最能近似刻画y与t之间关系的是( )
D [由题图知,该函数可能是y=lg2t.故选D.]
A.y=2t B.y=2t2 C.y=t3 D.y=lg2t
2.某种产品今年的产量是a,如果保持5%的年增长率,那么经过x年(x∈N*),该产品的产量y满足( )A.y=a(1+5%x) B.y=a+5%C.y=a(1+5%)x-1 D.y=a(1+5%)x
D [经过1年,y=a(1+5%);经过2年,y=a(1+5%)2;…;经过x年,y=a(1+5%)x.]
4.现测得(x,y)的两组对应值分别为(1,2),(2,5),现有两个待选模型,甲:y=x2+1,乙:y=3x-1,若又测得(x,y)的一组对应值为(3,10.2),则应选用_____作为函数模型.
甲 [将x=3分别代入y=x2+1及y=3x-1中,得y=32+1=10,y=3×3-1=8.由于10更接近10.2,所以选用甲模型.]
1.知识链:(1)应用已知函数模型解决实际问题.(2)指数型函数模型.(3)对数型函数模型.2.方法链:转化法.3.警示牌:实际应用题易忘记定义域和结论.
人教A版 (2019)必修 第一册4.5 函数的应用(二)教案配套ppt课件: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000277_t3/?tag_id=26" target="_blank">4.5 函数的应用(二)教案配套ppt课件</a>,共26页。PPT课件主要包含了学习目标,答案y=2x+1,答案e6-1,通性通法,提出问题,建立模型,检验模型,抽象概括,求解模型,还原说明等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)作业课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)作业课件ppt,共26页。PPT课件主要包含了ln2等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)教课ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)教课ppt课件,共38页。













