高中北师大版 (2019)1.2 集合的基本关系课文内容ppt课件

展开

这是一份高中北师大版 (2019)1.2 集合的基本关系课文内容ppt课件，共31页。PPT课件主要包含了封闭曲线，A⊆A等内容，欢迎下载使用。

1.2　集合的基本关系
必备知识·情境导学探新知
1．集合与集合之间的关系有哪几种？如何用符号表示这些关系？2．集合的子集是什么？真子集又是什么？如何用符号表示？
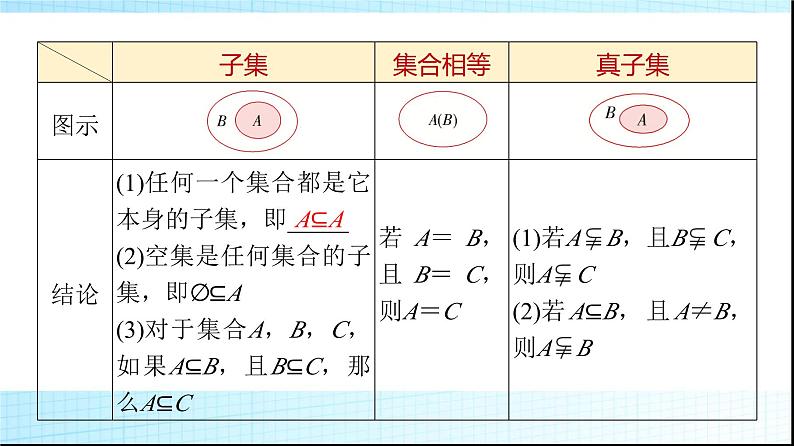
1．Venn图用平面上_________的内部表示集合，称为Venn图．2．子集、集合相等、真子集
思考(1)任何一个集合都有真子集吗？(2)∅与0，{0}，{∅}有何区别？
[提示]　(1)不是，空集没有真子集．(2)
体验1．已知集合P＝{－1，0，1，2}，Q＝{－1，0，1}，则(　　)A．P∈Q 　B．P⊆Q C．Q⊆P 　D．Q∈P
C　[集合Q中的元素都在集合P中，所以Q⊆P.]
体验2．已知集合A＝{x|－1A　[由题意结合集合在数轴上的表示确定两集合的关系即可．如图所示，B　A.
体验3．设a∈R，若集合{2，9}＝{1－a，9}，则a＝________．
－1　[因为{2，9}＝{1－a，9}，则2＝1－a，所以a＝－1.]
关键能力·合作探究释疑难
反思领悟　判断集合间关系的常用方法(1)列举观察法当集合中元素较少时，可列举出集合中的全部元素，通过定义得出集合之间的关系．(2)集合元素特征法先确定集合的代表元素是什么，弄清集合元素的特征，再利用集合元素的特征判断得出集合之间的关系．
一般地，设A＝{x|p(x)}，B＝{x|q(x)}，①若由p(x)可推出q(x)，则A⊆B；②若由q(x)可推出p(x)，则B⊆A；③若p(x)，q(x)可互相推出，则A＝B；④若由p(x)推不出q(x)，由q(x)也推不出p(x)，则集合A，B无包含关系．(3)数形结合法利用数轴或Venn图可清晰、明了地判断集合间的关系，其中不等式的解集之间的关系，适合用数轴法．
[跟进训练]1．(多选)下列关系中，正确的有(　　)A．0∈{0} 　B．∅　 {0}C．{0，1} 　{(0，1)} 　D．{(1，2)}＝{(2，1)}
AB　[对于A，集合{0}中含有1个元素0，所以0∈{0}正确；对于B，由于空集是任何非空集合的真子集，所以∅　{0}正确；对于C，{0，1}是数集，{(0，1)}是点集，所以C错误；对于D，{(1，2)}与{(2，1)}是不同的点集，所以D错误．]
2．能正确表示集合M＝{x∈R|0≤x≤2}和集合N＝{x∈R|x2－x＝0}关系的Venn图是(　　)
B　[解x2－x＝0得x＝1或x＝0，故N＝{0，1}，易得N　M，其对应的Venn图如选项B所示．]
A　　　　B　　　　C　　　　D
3．设M＝{x|x＝a2＋1，a∈R}，P＝{y|y＝b2－4b＋5，b∈R}，则下列关系正确的是(　　)A．M＝P 　B．M　PC．P　M 　D．M与P没有公共元素
A　[由a2＋1≥1得M＝{x|x≥1}，由b2－4b＋5＝(b－2)2＋1≥1得P＝{y|y≥1}，因此M＝P，故选A.]
类型2　子集个数问题【例2】　已知{1，2}　M⊆{1，2，3，4，5}，试写出满足条件的所有集合M.
[解]　集合M含有元素1，2，且含有3，4，5中的至少一个元素，依据集合元素的个数分类列举如下：含有3个元素：{1，2，3}，{1，2，4}，{1，2，5}；含有4个元素：{1，2，3，4}，{1，2，3，5}，{1，2，4，5}；含有5个元素：{1，2，3，4，5}.故满足条件的集合M共有上述7个集合．
反思领悟　求集合子集、真子集个数的3个步骤
[跟进训练]4．已知集合A＝{－1，0，1}，满足{0}⊆P⊆A的集合P的个数为(　　)A．2 　B．4 C．6 　D．8
B　[根据题意，集合P可以为{0}，{0，1}，{0，－1}，{－1，0，1}，共4个．]
5．已知集合A＝{(x，y)|x＋y＝2，x，y∈N}，试写出A的所有子集及真子集．
[解]　∵A＝{(x，y)|x＋y＝2，x∈N，y∈N}，∴A＝{(0，2)，(1，1)，(2，0)}，∴A的子集有∅，{(0，2)}，{(1，1)}，{(2，0)}，{(0，2)，(1，1)}，{(0，2)，(2，0)}，{(1，1)，(2，0)}，{(0，2)，(1，1)，(2，0)}．A的真子集有∅，{(0，2)}，{(1，1)}，{(2，0)}，{(0，2)，(1，1)}，{(0，2)，(2，0)}，{(1，1)，(2，0)}．
类型3　集合间的关系的应用【例3】　已知集合A＝{x|－2≤x≤7}，B＝{x|m＋1＜x＜2m－1}，且B⊆A，求实数m的取值范围．
[母题探究]1．对于本例中的集合A，B，是否存在实数m使A⊆B?
反思领悟　由集合的包含关系求参数的方法(1)当集合为不连续实数集时，常根据集合包含关系的意义，建立方程求解，此时应注意分类讨论；(2)当集合为连续实数集时，常借助数轴来建立不等关系求解，应注意端点处是实点还是虚点．注意：(1)不能忽视集合为∅的情形．(2)当集合中含有字母参数时，一般要分类讨论．
[跟进训练]6．已知集合A＝{x|x2＋x－6＝0}，B＝{x|mx＋1＝0}，B　A，求m的值．
阅读材料·拓展数学大视野
子集个数的探究观察下表并回答后面的问题．
1．若集合A有n个元素，则集合A有多少个子集？多少个真子集？多少个非空真子集？
[提示]　若集合A含有n个元素，则集合A有2n个子集；其真子集要去掉集合A本身，故有2n－1个；非空真子集要去掉集合A本身与空集，故有2n－2个．
2．对于有限集A，B，C，设集合A中含有n个元素，集合B中有m个元素(n，m∈N，且n>m)．(1)当B⊆C⊆A时，满足条件的C有多少个？(2)如果集合C分别满足如下条件：B⊆C　A，B　C⊆A，B　C　A，那么C的个数为多少？
[提示]　(1)由表格中的集合可知，若B⊆C⊆A，则集合C中一定有集合B的全部元素，也就是A中元素去掉B中元素后剩余元素构成的集合的子集，故有2n－m个．(2)①当B⊆C　A时，在问题(1)的基础上，去掉与A集合相等的集合，故满足条件的C有2n－m－1个．②当B　C⊆A时，在问题(1)的基础上，去掉与B集合相等的集合，故满足条件的C有2n－m－1个．③当B　C　A时，在问题(1)的基础上，去掉与A，B相等的两个集合，故有2n－m－2个．
学习效果·课堂评估夯基础
1．下列命题中正确的是(　　)A．空集没有子集B．空集是任何一个集合的真子集C．任何一个集合必有两个或两个以上的子集D．设集合B⊆A，那么，若x∉A，则x∉B
D　[空集有唯一一个子集，就是其本身，故A，C错误；空集是任何一个非空集合的真子集，故B错误；由子集的概念知D正确．]
2．已知集合A＝{x|x＝3k，k∈Z}，B＝{x|x＝6k，k∈Z}，则A与B之间的最适合的关系是(　　)A．A⊆B 　B．A⊇B C．A　B 　D．A　B
D　[集合A是能被3整除的整数组成的集合，集合B是能被6整除的整数组成的集合，所以B　A.]
C　[因为A＝{0，1，2}，所以其真子集的个数是23－1＝7.]
4．已知集合A⊆{0，1，2}，且集合A中至少含有一个偶数，则这样的集合A的个数为________．
6　[集合{0，1，2}的子集为：∅，{0}，{1}，{2}，{0，1}，{0，2}，{1，2}，{0，1，2}，其中含有偶数的集合有6个．]

相关课件更多