高中数学北师大版 (2019)必修 第一册4 指数函数、幂函数、对数函数增长的比较课堂教学ppt课件

这是一份高中数学北师大版 (2019)必修 第一册4 指数函数、幂函数、对数函数增长的比较课堂教学ppt课件，共27页。PPT课件主要包含了越来越快，越来越慢，指数爆炸等内容，欢迎下载使用。

必备知识·情境导学探新知
1．当a>1时，函数y＝ax的增长速度与a的大小有什么关系？2．当a>1时，函数y＝lgax的增长速度与a的大小有什么关系？3．当x>0，n>1时，函数y＝xn的增长速度与n的大小有什么关系？
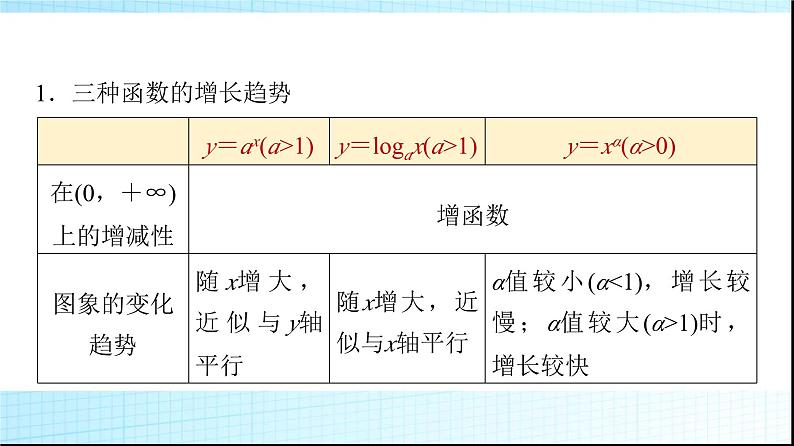
1．三种函数的增长趋势
2.当底数a>1时，由于指数函数y＝ax的值增长非常快，人们称这种现象为“________”．
思考 举例说明“指数爆炸”增长的含义．
[提示]　如1个细胞分裂x次后的数量为y＝2x，此为“指数增长”，其“增长量”是成倍增加的，从图象上看出，存在x0，当x>x0时，数量增加特别快，足以体现“爆炸”的效果．
体验1．思考辨析(正确的画“√”，错误的画“×”)(1)线性函数模型y＝kx＋b(k>0)的增长特点是直线上升，其增长速度不变．(　　)(2)指数函数模型y＝ax(a>1)的增长特点是随自变量的增大，函数值增大的速度越来越快．(　　)(3)对数函数模型y＝lgax(a>1)的增长特点是随自变量的增大，函数值增大的速度越来越慢．(　　)
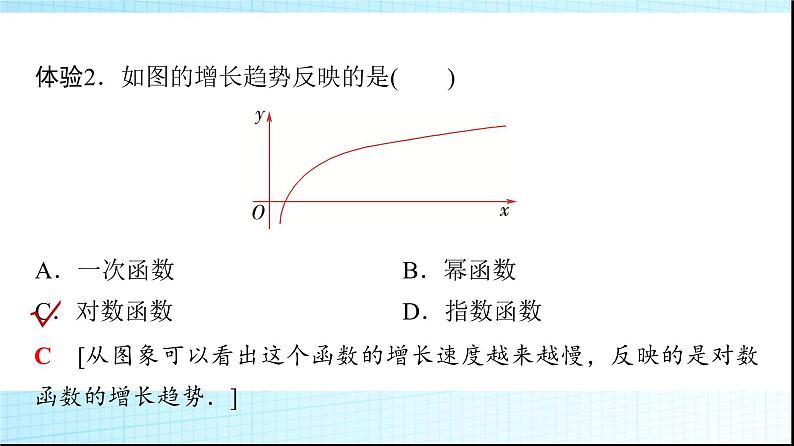
体验2．如图的增长趋势反映的是(　　)
C　[从图象可以看出这个函数的增长速度越来越慢，反映的是对数函数的增长趋势．]
A．一次函数 　B．幂函数C．对数函数 　D．指数函数
体验3．四个变量y1，y2，y3，y4随变量x变化的数据如下表：
关于x呈指数型函数变化的变量是________．
y2　[以爆炸式增长的变量是呈指数型函数变化的．从表格中可以看出，四个变量y1，y2，y3，y4均是从2开始变化，变量y1，y2，y3，y4都是越来越大，但是增长速度不同，其中变量y2的增长速度最快，画出它们的图象(图略)可知变量y2关于x呈指数型函数变化．]
关键能力·合作探究释疑难
类型1　指数函数、对数函数、幂函数图象的比较【例1】　函数f (x)＝2x和g(x)＝x3的图象如图所示．设两函数的图象交于点A(x1，y1)，B(x2，y2)，且x1(1)请指出示意图中曲线C1，C2分别对应哪一个函数；(2)结合函数图象，比较f (8)，g(8)，f (2 022)，g(2 022)的大小．
[解]　(1)C1对应的函数为g(x)＝x3，C2对应的函数为f (x)＝2x.(2)∵g(1)＝1，f (1)＝2，g(2)＝8，f (2)＝4，g(9)＝729，f (9)＝512，g(10)＝1 000，f (10)＝1 024，∴f (1)>g(1)，f (2)g(10)．∴1x2时，f (x)>g(x)，且g(x)在(0，＋∞)上单调递增，∴f (2 022)>g(2 022)>g(8)>f (8)．
反思领悟　底数大于1的指数函数模型和幂指数大于1的幂函数模型都是增函数，增长的快慢交替出现，从这个实例我们可以体会到幂函数增长，指数爆炸等不同函数模型增大的含义．
C　[a，c对应的是幂函数，a的指数大于1，c的指数大于0小于1；b和d对应的函数是指数函数，且b中的底数大于1，d中的底数大于0小于1.]
类型2　几类函数模型增长差异的比较【例2】　已知三个变量y1，y2，y3随变量x变化的数据如下表：
B　[从题中表格可以看出，三个变量y1，y2，y3都是越来越大，但是增长速度不同，其中变量y1的增长速度最快，呈指数型函数变化，变量y3的增长速度最慢，呈对数型函数变化．]
则反映y1，y2，y3随x变化情况拟合较好的一组函数模型是(　　)A．y1＝x2，y2＝2x，y3＝lg2x　B．y1＝2x，y2＝x2，y3＝lg2xC．y1＝lg2x，y2＝x2，y3＝2x　D．y1＝2x，y2＝lg2x，y3＝x2
反思领悟　常见的函数模型及增长特点(1)线性函数模型线性函数模型y＝kx＋b(k>0)的增长特点是直线上升，其增长速度不变．(2)指数函数模型指数函数模型y＝ax(a>1)的增长特点是随着自变量的增大，函数值增大的速度越来越快，即增长速度急剧，形象地称为“指数爆炸”．(3)对数函数模型对数函数模型y＝lgax(a>1)的增长特点是随着自变量的增大，函数值增大的速度越来越慢，即增长速度平缓．(4)幂函数模型幂函数y＝xn(n>0)的增长速度介于指数增长和对数增长之间．
[跟进训练]2．四个物体同时从某一点出发向前运动，其路程f i(x)(i＝1，2，3，4)关于时间x(x>1)的函数关系是f 1(x)＝x2，f 2(x)＝2x，f 3(x)＝lg2x，f 4(x)＝2x，如果它们一直运动下去，最终在最前面的物体具有的函数关系是(　　)A．f 1(x)＝x2 　B．f 2(x)＝2xC．f 3(x)＝lg2x 　D．f 4(x)＝2x
D　[由增长速度可知，当自变量充分大时，指数函数的值最大．故选D.]
类型3　函数模型的构建【例3】　假设你有一笔资金用于投资，现有三种投资方案供你选择，这三种方案的回报如下：方案一：每天回报40元；方案二：第一天回报10元，以后每天比前一天多回报10元；方案三：第一天回报0.4元，以后每天的回报比前一天翻一番．请问，你会选择哪种投资方案？
[解]　设第x天所得回报是y元．由题意，方案一：y＝40(x∈N＋)；方案二：y＝10x(x∈N＋)；方案三：y＝0.4×2x-1(x∈N＋)．作出三个函数的图象如图：由图可以看出，从每天回报看，在第一天到第三天，方案一最多，在第四天，方案一、二一样多，方案三最少，在第五天到第八天，方案二最多，第九天开始，方案三比其他两个方案所得回报多得多，经验证到第三十天，所得回报已超过2亿元，
∴若是短期投资可选择方案一或方案二，长期的投资则选择方案三．通过计算器计算列出三种方案的累积收入表．
∴投资一天到六天，应选方案一，投资七天方案一、二均可，投资八天到十天应选方案二，投资十一天及其以上，应选方案三．
反思领悟　函数模型构建的一般步骤(1)收集数据．(2)根据收集到的数据，在平面直角坐标系内画出散点图．(3)根据点的分布特征，选择一个能刻画散点图特征的函数模型．(4)选择其中的几组数据求出函数模型．(5)将已知数据代入所求出的函数模型中进行检验，看其是否符合实际，若不符合实际，则返回步骤(3)；若符合实际，则进入下一步．(6)用所得函数模型分析实际问题．
[跟进训练]3．某人对东北一种松树的生长进行了研究，收集了其高度h(米)与生长时间t(年)的相关数据，选择h＝mt＋b与h＝lga(t＋1)来刻画h与t的关系，你认为哪个符合？并预测第8年的松树高度．
[解]　根据表中数据作出散点图如图：由图可以看出用一次函数模型不吻合，选用对数型函数比较合理．将(2，1)代入到h＝lga(t＋1)中，得1＝lga3，解得a＝3．即h＝lg3(t＋1)．当t＝8时，h＝lg3(8＋1)＝2，故可预测第8年松树的高度为2米．
学习效果·课堂评估夯基础
2．下列函数中，增长速度越来越慢的是(　　)A．y＝6x 　B．y＝lg6xC．y＝x6 　D．y＝6x
B　[D中一次函数的增长速度不变，A、C中函数的增长速度越来越快，只有B中对数函数的增长速度越来越慢，符合题意．]
3．以下四种说法中，正确的是(　　)A．幂函数增长的速度比一次函数增长的速度快B．对任意的x>0，xn>lgaxC．对任意的x>0，ax>lgaxD．不一定存在x0，当x>x0时，总有ax>xn>lgax
D　[对于A，幂函数与一次函数的增长速度受幂指数及一次项系数的影响，幂指数与一次项系数不确定，增长幅度不能比较；对于B、C，当01，n>0时，一定存在x0，使得当x>x0时，总有ax>xn>lgax，但若去掉限制条件“a>1，n>0”，则结论不一定成立．]
4．已知函数f (x)＝3x，g(x)＝2x，当x∈R时，f (x)与g(x)的大小关系为__________．
f (x)>g(x)　[在同一直角坐标系中画出函数f (x)＝3x，g(x)＝2x的图象，如图所示，  由于函数f (x)＝3x的图象始终在函数g(x)＝2x图象的上方，则f (x)>g(x)．]
f (x)>g(x)