高中数学北师大版 (2019)必修 第一册1.2 利用二分法求方程的近似解教学演示ppt课件

这是一份高中数学北师大版 (2019)必修 第一册1.2 利用二分法求方程的近似解教学演示ppt课件，共30页。PPT课件主要包含了f025等内容，欢迎下载使用。

必备知识·情境导学探新知
1．若x0是满足精度ε的近似值，则x0应满足什么条件？2．二分法的定义是什么？3．如何用二分法求函数的零点或方程的近似解？
f (a)·f (b)<0
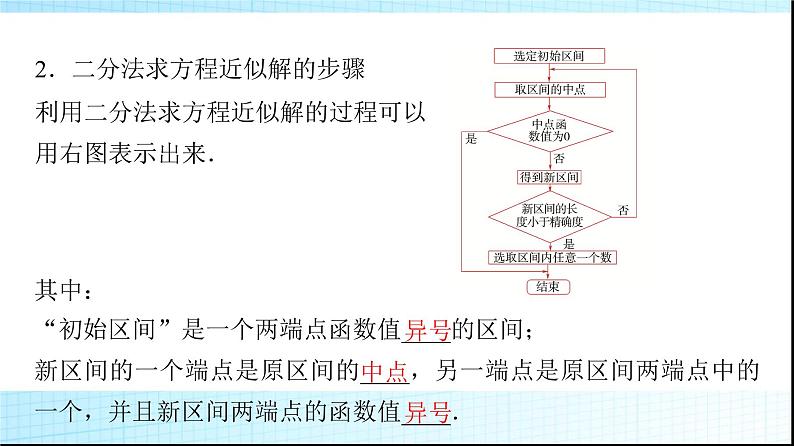
2．二分法求方程近似解的步骤利用二分法求方程近似解的过程可以用右图表示出来．
其中：“初始区间”是一个两端点函数值____的区间；新区间的一个端点是原区间的____，另一端点是原区间两端点中的一个，并且新区间两端点的函数值____．
思考　(1)所有函数的零点都可以用二分法求出吗？(2)“精确到0.1”与“精确度为0.1”一样吗？
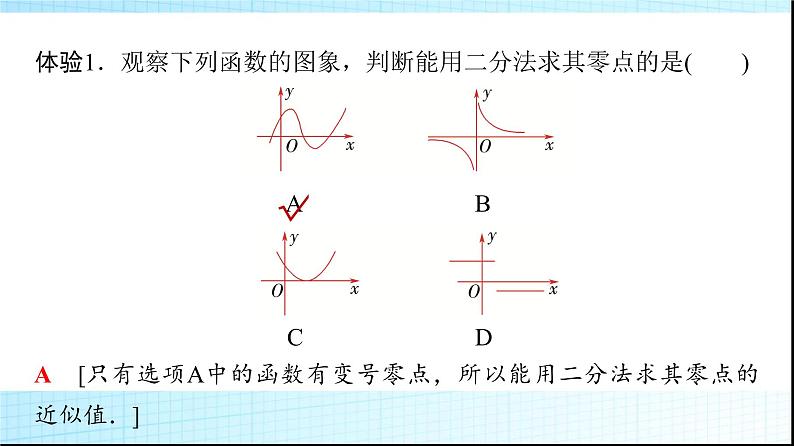
体验1．观察下列函数的图象，判断能用二分法求其零点的是(　　)
A　[只有选项A中的函数有变号零点，所以能用二分法求其零点的近似值．]
体验2．用二分法求函数f (x)＝x3＋5的零点可以取的初始区间是(　　)A．(－2，－1) 　B．(－1，0)C．(0，1) 　D．(1，2)
A　[∵f (－2)＝－3<0，f (－1)＝4>0，f (－2)·f (－1)<0，故可取(－2，－1)作为初始区间，用二分法逐次计算．]
关键能力·合作探究释疑难
类型1　二分法的概念理解【例1】　下列图象与x轴均有交点，其中不能用二分法求函数零点的是(　　)
A　[按定义，f (x)在[a，b]上是连续的，且f (a)·f (b)<0，才能不断地把函数零点所在的区间一分为二，进而利用二分法求出函数的零点．故结合各图象可得选项B、C、D满足条件，而选项A不满足，在A中，图象经过零点x0时，函数值不变号，因此不能用二分法求解．故选A.]
反思领悟　判断一个函数能否用二分法求其零点的依据是：其图象在零点附近是连续不断的，且该零点为变号零点．因此，用二分法求函数的零点近似值的方法仅对函数的变号零点适合，对函数的不变号零点不适合．
[跟进训练]1．下列函数中能用二分法求零点的为(　　)
B　[函数图象连续不断，函数零点附近的函数值异号，这样的函数零点才能使用二分法求解，观察四个函数图象，只有B选项符合．]
A　　　 　B　　 　　　C　　　 　D
类型2　利用二分法求方程的近似解【例2】　求方程x3－3＝0的一个近似解．(精确度为0.02)
[思路点拨]　利用二分法求解．
[解]　考查函数f (x)＝x3－3，基于零点存在定理，从一个两端点函数值异号的区间开始，应用二分法逐步缩小方程解所在的区间．经计算f (1)＝－2<0，f (2)＝5＞0，所以方程x3－3＝0在区间(1，2)内有解．取区间(1，2)的中点1.5，f (1.5)＝0.375＞0，所以方程x3－3＝0在区间(1，1.5)内有解．
如此下去，得到方程x3－3＝0的解所在区间(如下表)：
至此可以看出区间[1.437 5，1.453 125]的区间长度小于0.02，而方程的近似解就在这个区间内，因此区间内任意一个数都是满足精确度的近似解，例如，1.45就是方程x3－3＝0精确度为0.02的一个近似解．
[母题探究]1．本例变为：根据下表，用二分法求函数f (x)＝x3－3x＋1在区间(1，2)上的零点的近似值(精确度为0.1)是________．
1.5　[由表中数据知f (1.5)·f (2)<0，f (1.5)·f (1.562 5)<0，所以函数零点在区间(1.5，1.562 5)上，又因为|1.562 5－1.5|＝0.062 5<0.1，所以函数f (x)＝x3－3x＋1在区间(1，2)上的零点的近似值可以取1.5.]
用二分法逐次计算，列表如下：
反思领悟1．用二分法求方程近似解应遵循的原则(1)需依据图象估计零点所在的初始区间[m，n](一般采用估计值的方法完成)．(2)取区间端点的中点c，计算f (c)，确定有解区间是(m，c)还是(c，n)，逐步缩小区间的“长度”，直到区间的两个端点符合精确度要求，终止计算，得到函数零点的近似值．2．二分法求方程近似解步骤的记忆口诀定区间，找中点，中值计算两边看．同号丢，异号算，零点落在异号间．重复做，何时止，利用精度把关口．
[跟进训练]2．用二分法求方程2x3＋3x－3＝0的一个正实数近似解．(精确度为0.1)
[解]　令f (x)＝2x3＋3x－3，经计算，f (0)＝－3<0，f (1)＝2>0，f (0)·f (1)<0，所以函数f (x)在(0，1)内存在零点，即方程2x3＋3x－3＝0在(0，1)内有解．取(0，1)的中点0.5，经计算f (0.5)<0，又f (1)>0，所以方程2x3＋3x－3＝0在(0.5，1)内有解．
如此继续下去，得到方程的正实数根所在的区间，如表：
由于|0.687 5－0.75|＝0.062 5<0.1，所以0.75可作为方程的一个正实数近似解．
阅读材料·拓展数学大视野
二分法的实际应用乒乓球是两个半圆的球粘成的，好的乒乓球在黏合时是加热的，所以里面有塑料和胶水的气味，乒乓球虽小，但打时的速度快，变化多，技术要求高，特别是对判断力的锻炼，要求运动员眼疾手快，抓住稍纵即逝的机会，对培养顽强拼搏的精神，很有好处．因此，乒乓球已经成为一项世界性、普遍性的体育运动．现有a个乒乓球，从外观上看完全相同，除了1个乒乓球质量不符合标准外，其余的乒乓球质量均相同．你能尽快把这个“坏乒乓球”找出来吗？用一架天平，限称b次，并说明此乒乓球是偏轻还是偏重．
1．当a＝12，b＝3时，该如何称？
[提示]　第一次，天平左右各放4个乒乓球，有两种情况：(1)若平，则“坏乒乓球”在剩下的4个乒乓球中．第二次，取剩下的4个乒乓球中的3个乒乓球为一边，取3个好乒乓球为另一边，放在天平上．①若仍平，则“坏乒乓球”为剩下的4个乒乓球中未取到的那个乒乓球，将此乒乓球与1个好乒乓球放上天平一看，即知“坏乒乓球”是偏轻还是偏重；
②若不平，则“坏乒乓球”在取出的3个乒乓球之中，且知是轻还是重．任取其中2个乒乓球放在天平上，无论平还是不平，均可确定“坏乒乓球”．(2)若不平，则“坏乒乓球”在天平上的8个乒乓球中，不妨设右边较重．从右边4个乒乓球中取出3个乒乓球置于一容器内，然后从左边4个乒乓球中取3个乒乓球移入右边，再从外面好乒乓球中取3个乒乓球补入左边．看天平，有三种可能．①若平，则“坏乒乓球”是容器内3个乒乓球之一且偏重；
②若左边重，“坏乒乓球”已从一边换到另一边．因此，“坏乒乓球”只能是从左边移入右边的3个乒乓球之一，并且偏轻；③若右边重，据此知“坏乒乓球”未变动位置，而未被移动过的乒乓球只有两个(左右各一)，“坏乒乓球”是其中之一(暂不知是轻还是重)．显然对于以上三种情况的任一种，再用一次天平，即可找出“坏乒乓球”，且知其是轻还是重．
2．若“坏乒乓球偏轻”，当a＝26时，求b的最大值．
[提示]　将26枚乒乓球平均分成两份，分别放在天平两端，则“坏乒乓球”一定在质量小的那13个乒乓球里面；从这13个乒乓球中拿出1个，然后将剩下的12个乒乓球平均分成两份，分别放在天平两端，若天平平衡，则“坏乒乓球”一定是拿出的那一个，若天平不平衡，则“坏乒乓球”一定在质量小的那6个乒乓球里面；将这6个乒乓球平均分成两份，分别放在天平两端，则“坏乒乓球”一定在质量小的那3个乒乓球里面；从这3个乒乓球中任拿出2个，分别放在天平两端，若天平平衡，则剩下的那一个即是“坏乒乓球”，若天平不平衡，则质量小的那一枚即是“坏乒乓球”．综上可知，最多称4次就可以发现这个“坏乒乓球”．
学习效果·课堂评估夯基础
1．思考辨析(正确的画“√”，错误的画“×”)(1)二分法所求出的方程的解都是近似解．(　　)(2)函数f (x)＝|x|可以用二分法求零点．(　　)(3)用二分法求函数零点的近似值时，每次等分区间后，零点必定在右侧区间．(　　)
[提示]　(1)错误．如函数f (x)＝x－2用二分法求出的解就是精确解．(2)错误．对于函数f (x)＝|x|，不存在区间(a，b)，使f (a)f (b)<0，所以不能用二分法求其零点．(3)错误. 函数的零点也可能是区间的中点或在左侧区间内．
2．已知定义在R上的函数f (x)的图象是连续不断的，且有如下对应值表：
B　[因为f (1)＞0，f (2)＜0，由零点存在定理可知f (x)一定存在零点的区间是(1，2)．]
那么函数f (x)一定存在零点的区间是(　　)A．(0，1) 　B．(1，2)C．(2，3) 　D．(3，＋∞)
4．用二分法研究函数f (x)＝x3＋3x－1的零点时，第一次经计算得f (0)<0，f (0.5)>0，可得其中一个零点x0∈________，第二次应计算__________．