





还剩15页未读,
继续阅读
所属成套资源:全套北师大版七年级数学上册提优小卷课件
成套系列资料,整套一键下载
北师大版七年级数学上册提优小卷(11)一元一次方程的应用课件
展开
这是一份北师大版七年级数学上册提优小卷(11)一元一次方程的应用课件,共23页。
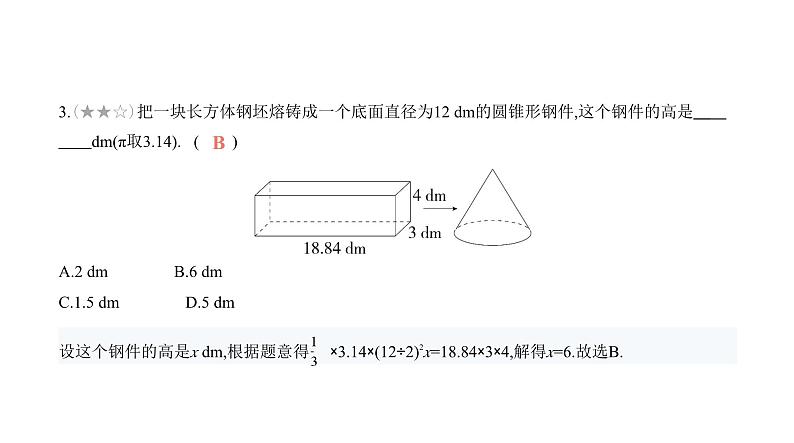
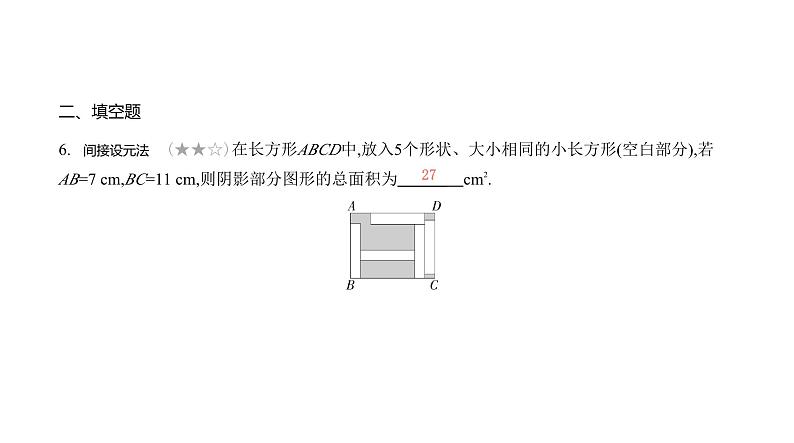
提优小卷(11)一元一次方程的应用一、选择题1. 情境题 数学文化 (2024重庆梁平中学期末,8,★★☆)中国古代人民很早就在生产生活中发 现了许多有趣的数学问题,《孙子算经》中有这样一个问题:今有三人共车,二车空;二人共车,九 人步,问人与车各几何.这道题的意思是:今有若干人乘车,每三人共乘一辆车,则剩余两辆车是空 的;每两人共乘一辆车,则剩余九个人无车可乘,问车和人各多少.若设有x辆车,则可列方程为( )A.3(x-2)=2x+9 B.3(x+2)=2x-9C. +2= D. -2= A根据题意可列方程为3(x-2)=2x+9.故选A.2.(2024四川南充四校期末联考,8,★★☆)某市对迎宾大道进行绿化,计划把某一段公路的一侧全 部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔3米栽1棵,则树苗缺1 5棵;如果每隔4米栽1棵,则树苗缺1棵,则树苗的棵数是( )A.41 B.42 C.43 D.44B设有树苗x棵,则3(x+15-1)=4(x+1-1),解得x=42,故选B.3.(★★☆)把一块长方体钢坯熔铸成一个底面直径为12 dm的圆锥形钢件,这个钢件的高是 dm(π取3.14). ( )A.2 dm B.6 dm C.1.5 dm D.5 dmB4. 跨学科 历史 (★★☆)“曹冲称象”是流传很广的故事,过程大致如下:先将大象牵到大船 上,并在船侧面标记水位,再将大象牵出,然后往船上抬入20块等重的条形石,并在船上留3个搬运 工,这时水位恰好到达标记位置,如果再抬入1块同样的条形石,船上只留1个搬运工,水位也恰好 到达标记位置.已知搬运工体重均为60千克,则每块条形石的质量是 ( )A.60千克 B.120千克 C.50千克 D.80千克B设每块条形石的质量是x千克,根据题意得20x+60×3=21x+60,解得x=120,所以每块条形石的质量是120千克.故选B.5.(2024山东临沂期末,12,★★☆)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根 露出水面的长度是它的 ,另一根露出水面的长度是它的 ,若两根铁棒长度差为20 cm,有下列说法:①两根铁棒的长度和为340 cm;②其中一根铁棒的长度为170 cm;③两根铁棒的长度和为440 cm;④其中一根铁棒露出水面的长度为60 cm.其中说法正确的个数为 ( ) A.0 B.3 C.2 D.1C设较长铁棒的长度为x cm,则较短铁棒的长度为(x-20)cm,由题意得 x= (x-20),解得x=180,所以较长铁棒的长度为180 cm,较短铁棒的长度为160 cm,故②错误;两根铁棒的长度和为180+160=340(cm),故①正确,③错误;较长铁棒露出水面的长度为180× =60(cm),故④正确.因此正确的说法是①④,共2个.故选C.二、填空题6. 间接设元法 (★★☆)在长方形ABCD中,放入5个形状、大小相同的小长方形(空白部分),若 AB=7 cm,BC=11 cm,则阴影部分图形的总面积为 cm2. 27设小长方形的长为x cm,则宽为(7-x)cm,根据题意得x+3(7-x)=11,解得x=5,所以x(7-x)=5×2=10,即每个小长方形的面积为10 cm2,所以阴影部分图形的总面积=7×11-5×10=27(cm2).7. 直接设元法 (2024四川绵阳期末,18,★★☆)姐姐比弟弟大3岁,若5年前姐姐的年龄是弟弟的2 倍,则姐姐现在的年龄是 岁.11设姐姐现在的年龄是x岁,则弟弟现在的年龄是(x-3)岁,根据题意得x-5=2(x-3-5),解得x=11,即姐姐现在的年龄是11岁.8.(2024辽宁盘锦大洼期末,15,★★☆)12月4日为全国法制宣传日,某校组织全体学生参加法制知 识竞赛,共设20道选择题(各题分值相同),每题必答,下表记录了其中3名参赛者的得分情况,若参 赛者D的得分为76分,则他答对了 道题.16设答对一道题得x分,答错一道题扣y分,参赛者D答对了z道题,由题意得20x=100,解得x=5,所以18×5-2y=88,解得y=1,所以5z-1×(20-z)=76,解得z=16,所以参赛者D答对了16道题.9.(★★☆)一个两位数的各位数字之和为8,十位数字与个位数字互换后,所得新数比原数小18,则 原来的两位数是 .53设原两位数的个位数字为x,则十位数字为8-x,根据题意,得[10(8-x)+x]-[10x+(8-x)]=18,解得x=3,则原来的两位数是10(8-x)+x=53.10. 数形结合思想 (★★★)如图,一个容积为480毫升的玻璃瓶里装有一些水,正立放置时水面 高度为11 cm(玻璃瓶的下半部分看成是圆柱体),倒立放置时上部空余部分的高度是5 cm,那么瓶 内的水有 毫升.(提示:1毫升=1立方厘米) 330设瓶子的底面积为x cm2,根据题意,得(11+5)x=480,解得x=30,30×11=330(毫升),即瓶内的水有330毫升.三、解答题11.(★★☆)春节在即,公司计划安排甲、乙两个小组分别生产和包装某种礼品,已知两组共50人, 且甲组人数比乙组人数的2倍少4人.(1)求甲、乙两组各多少人.(2)若每个工人每天可生产300个礼品或包装700个礼品,为使每天生产的礼品恰好包装完,应从乙 组中调配几个人到甲组?(1)设乙组有x人,则甲组有(2x-4)人,由题意可得2x-4+x=50,解得x=18,∴2x-4=32.答:甲组有32人,乙组有18人.(2)设应从乙组中调配m个人到甲组,由题意可得300(32+m)=700(18-m).解得m=3.答:应从乙组中调配3个人到甲组.12.(★★☆)小明和小强两人在学校400 米长的环形操场跑道匀速跑步,小明的速度是小强的1.5 倍.两人同时从同一起点同向出发,4分钟后小明第一次追上小强.(1)求小明和小强两人跑步的速度.(2)如果小明和小强两人同时从同一起点背向出发,经过多长时间两人恰好第三次相遇?(1)设小强跑步的速度为x 米/分钟,则小明跑步的速度为1.5x米/分钟.由题意得4(1.5x-x)=400,解得x=200.所以1.5x=300.答:小明跑步的速度为300 米/分钟,小强跑步的速度为200 米/分钟.(2)设经过y分钟两人恰好第三次相遇,由题意得(200+300)y=400×3,解得y= .答:经过 分钟两人恰好第三次相遇.13.(★★☆)“爱读书,读好书,善读书”正成为全民的追求,某书城老板看到了此中的商机,准备 购进甲、乙两类畅销书刊.第一次该书城购进1 000本甲类书刊和500本乙类书刊,费用为28 000 元,甲类书刊每本的进价比乙类书刊多4元.书城决定甲、乙两类书刊均按进价的1.5倍标价销售.(1)求甲、乙两类书刊每本的进价各是多少元.(2)该书城第一次购进的甲、乙两类书刊很快售完,第二次以同样的价格购进了与上次同样数量 的甲、乙两类书刊.一段时间后,甲类书刊销售缓慢,只卖出了400本,老板决定对剩余的甲类书刊 打折出售,乙类书刊价格不变,最后全部售完,总利润比第一次少3 600元,求剩余的甲类书刊打了 几折.(1)设乙类书刊每本的进价为x元,则甲类书刊每本的进价为(x+4)元,根据题意,得1 000(x+4)+500x=28 000,解得x=16,所以x+4=16+4=20.答:甲类书刊每本的进价是20元,乙类书刊每本的进价是16元.(2)第一次的总利润为1 000×20×0.5+500×16×0.5=14 000(元),设剩余的甲类书刊打了a折,由题意得500×16×0.5+400×20×0.5+(1 000-400)× =14 000-3 600,解得a=8.答:剩余的甲类书刊打了八折.14.(2024云南昭通学院附中期末,24,★★☆)春节历史悠久,由上古时代岁首祈年祭祀演变而来. 某工厂计划生产A、B两种喜迎新春产品共140件,其中A种产品的件数比B种产品件数的3倍少20 件.(1)求工厂计划生产A、B两种新春产品各多少件.(2)现在工厂需要购买甲、乙两种材料生产新春产品.甲种材料的售价为每千克5元,乙种材料的 售价为每千克3元,采购员小李分两次购买完所需的材料,第一次购买两种材料共200千克,受市场 价格影响,第二次购买时甲材料的价格为每千克4元,乙材料的价格不变.①设采购员第一次购买甲种材料m千克,填表:②若第二次购买材料的费用比第一次购买材料的费用多500元,求采购员第一次购买甲种材料多 少千克.(1)设工厂计划生产B种产品x件,则工厂计划生产A种产品(3x-20)件,根据题意,得3x-20+x=140,解得x=40,所以3x-20=100.答:工厂计划生产A种产品100件,生产B种产品40件.(2)①380-m;m-20.②第一次购买材料的费用为5m+3(200-m)=(600+2m)元,第二次购买材料的费用为4(380-m)+3(m-20)=(1 460-m)元,所以1 460-m=600+2m+500,解得m=120.答:采购员第一次购买甲种材料120千克.
提优小卷(11)一元一次方程的应用一、选择题1. 情境题 数学文化 (2024重庆梁平中学期末,8,★★☆)中国古代人民很早就在生产生活中发 现了许多有趣的数学问题,《孙子算经》中有这样一个问题:今有三人共车,二车空;二人共车,九 人步,问人与车各几何.这道题的意思是:今有若干人乘车,每三人共乘一辆车,则剩余两辆车是空 的;每两人共乘一辆车,则剩余九个人无车可乘,问车和人各多少.若设有x辆车,则可列方程为( )A.3(x-2)=2x+9 B.3(x+2)=2x-9C. +2= D. -2= A根据题意可列方程为3(x-2)=2x+9.故选A.2.(2024四川南充四校期末联考,8,★★☆)某市对迎宾大道进行绿化,计划把某一段公路的一侧全 部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔3米栽1棵,则树苗缺1 5棵;如果每隔4米栽1棵,则树苗缺1棵,则树苗的棵数是( )A.41 B.42 C.43 D.44B设有树苗x棵,则3(x+15-1)=4(x+1-1),解得x=42,故选B.3.(★★☆)把一块长方体钢坯熔铸成一个底面直径为12 dm的圆锥形钢件,这个钢件的高是 dm(π取3.14). ( )A.2 dm B.6 dm C.1.5 dm D.5 dmB4. 跨学科 历史 (★★☆)“曹冲称象”是流传很广的故事,过程大致如下:先将大象牵到大船 上,并在船侧面标记水位,再将大象牵出,然后往船上抬入20块等重的条形石,并在船上留3个搬运 工,这时水位恰好到达标记位置,如果再抬入1块同样的条形石,船上只留1个搬运工,水位也恰好 到达标记位置.已知搬运工体重均为60千克,则每块条形石的质量是 ( )A.60千克 B.120千克 C.50千克 D.80千克B设每块条形石的质量是x千克,根据题意得20x+60×3=21x+60,解得x=120,所以每块条形石的质量是120千克.故选B.5.(2024山东临沂期末,12,★★☆)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根 露出水面的长度是它的 ,另一根露出水面的长度是它的 ,若两根铁棒长度差为20 cm,有下列说法:①两根铁棒的长度和为340 cm;②其中一根铁棒的长度为170 cm;③两根铁棒的长度和为440 cm;④其中一根铁棒露出水面的长度为60 cm.其中说法正确的个数为 ( ) A.0 B.3 C.2 D.1C设较长铁棒的长度为x cm,则较短铁棒的长度为(x-20)cm,由题意得 x= (x-20),解得x=180,所以较长铁棒的长度为180 cm,较短铁棒的长度为160 cm,故②错误;两根铁棒的长度和为180+160=340(cm),故①正确,③错误;较长铁棒露出水面的长度为180× =60(cm),故④正确.因此正确的说法是①④,共2个.故选C.二、填空题6. 间接设元法 (★★☆)在长方形ABCD中,放入5个形状、大小相同的小长方形(空白部分),若 AB=7 cm,BC=11 cm,则阴影部分图形的总面积为 cm2. 27设小长方形的长为x cm,则宽为(7-x)cm,根据题意得x+3(7-x)=11,解得x=5,所以x(7-x)=5×2=10,即每个小长方形的面积为10 cm2,所以阴影部分图形的总面积=7×11-5×10=27(cm2).7. 直接设元法 (2024四川绵阳期末,18,★★☆)姐姐比弟弟大3岁,若5年前姐姐的年龄是弟弟的2 倍,则姐姐现在的年龄是 岁.11设姐姐现在的年龄是x岁,则弟弟现在的年龄是(x-3)岁,根据题意得x-5=2(x-3-5),解得x=11,即姐姐现在的年龄是11岁.8.(2024辽宁盘锦大洼期末,15,★★☆)12月4日为全国法制宣传日,某校组织全体学生参加法制知 识竞赛,共设20道选择题(各题分值相同),每题必答,下表记录了其中3名参赛者的得分情况,若参 赛者D的得分为76分,则他答对了 道题.16设答对一道题得x分,答错一道题扣y分,参赛者D答对了z道题,由题意得20x=100,解得x=5,所以18×5-2y=88,解得y=1,所以5z-1×(20-z)=76,解得z=16,所以参赛者D答对了16道题.9.(★★☆)一个两位数的各位数字之和为8,十位数字与个位数字互换后,所得新数比原数小18,则 原来的两位数是 .53设原两位数的个位数字为x,则十位数字为8-x,根据题意,得[10(8-x)+x]-[10x+(8-x)]=18,解得x=3,则原来的两位数是10(8-x)+x=53.10. 数形结合思想 (★★★)如图,一个容积为480毫升的玻璃瓶里装有一些水,正立放置时水面 高度为11 cm(玻璃瓶的下半部分看成是圆柱体),倒立放置时上部空余部分的高度是5 cm,那么瓶 内的水有 毫升.(提示:1毫升=1立方厘米) 330设瓶子的底面积为x cm2,根据题意,得(11+5)x=480,解得x=30,30×11=330(毫升),即瓶内的水有330毫升.三、解答题11.(★★☆)春节在即,公司计划安排甲、乙两个小组分别生产和包装某种礼品,已知两组共50人, 且甲组人数比乙组人数的2倍少4人.(1)求甲、乙两组各多少人.(2)若每个工人每天可生产300个礼品或包装700个礼品,为使每天生产的礼品恰好包装完,应从乙 组中调配几个人到甲组?(1)设乙组有x人,则甲组有(2x-4)人,由题意可得2x-4+x=50,解得x=18,∴2x-4=32.答:甲组有32人,乙组有18人.(2)设应从乙组中调配m个人到甲组,由题意可得300(32+m)=700(18-m).解得m=3.答:应从乙组中调配3个人到甲组.12.(★★☆)小明和小强两人在学校400 米长的环形操场跑道匀速跑步,小明的速度是小强的1.5 倍.两人同时从同一起点同向出发,4分钟后小明第一次追上小强.(1)求小明和小强两人跑步的速度.(2)如果小明和小强两人同时从同一起点背向出发,经过多长时间两人恰好第三次相遇?(1)设小强跑步的速度为x 米/分钟,则小明跑步的速度为1.5x米/分钟.由题意得4(1.5x-x)=400,解得x=200.所以1.5x=300.答:小明跑步的速度为300 米/分钟,小强跑步的速度为200 米/分钟.(2)设经过y分钟两人恰好第三次相遇,由题意得(200+300)y=400×3,解得y= .答:经过 分钟两人恰好第三次相遇.13.(★★☆)“爱读书,读好书,善读书”正成为全民的追求,某书城老板看到了此中的商机,准备 购进甲、乙两类畅销书刊.第一次该书城购进1 000本甲类书刊和500本乙类书刊,费用为28 000 元,甲类书刊每本的进价比乙类书刊多4元.书城决定甲、乙两类书刊均按进价的1.5倍标价销售.(1)求甲、乙两类书刊每本的进价各是多少元.(2)该书城第一次购进的甲、乙两类书刊很快售完,第二次以同样的价格购进了与上次同样数量 的甲、乙两类书刊.一段时间后,甲类书刊销售缓慢,只卖出了400本,老板决定对剩余的甲类书刊 打折出售,乙类书刊价格不变,最后全部售完,总利润比第一次少3 600元,求剩余的甲类书刊打了 几折.(1)设乙类书刊每本的进价为x元,则甲类书刊每本的进价为(x+4)元,根据题意,得1 000(x+4)+500x=28 000,解得x=16,所以x+4=16+4=20.答:甲类书刊每本的进价是20元,乙类书刊每本的进价是16元.(2)第一次的总利润为1 000×20×0.5+500×16×0.5=14 000(元),设剩余的甲类书刊打了a折,由题意得500×16×0.5+400×20×0.5+(1 000-400)× =14 000-3 600,解得a=8.答:剩余的甲类书刊打了八折.14.(2024云南昭通学院附中期末,24,★★☆)春节历史悠久,由上古时代岁首祈年祭祀演变而来. 某工厂计划生产A、B两种喜迎新春产品共140件,其中A种产品的件数比B种产品件数的3倍少20 件.(1)求工厂计划生产A、B两种新春产品各多少件.(2)现在工厂需要购买甲、乙两种材料生产新春产品.甲种材料的售价为每千克5元,乙种材料的 售价为每千克3元,采购员小李分两次购买完所需的材料,第一次购买两种材料共200千克,受市场 价格影响,第二次购买时甲材料的价格为每千克4元,乙材料的价格不变.①设采购员第一次购买甲种材料m千克,填表:②若第二次购买材料的费用比第一次购买材料的费用多500元,求采购员第一次购买甲种材料多 少千克.(1)设工厂计划生产B种产品x件,则工厂计划生产A种产品(3x-20)件,根据题意,得3x-20+x=140,解得x=40,所以3x-20=100.答:工厂计划生产A种产品100件,生产B种产品40件.(2)①380-m;m-20.②第一次购买材料的费用为5m+3(200-m)=(600+2m)元,第二次购买材料的费用为4(380-m)+3(m-20)=(1 460-m)元,所以1 460-m=600+2m+500,解得m=120.答:采购员第一次购买甲种材料120千克.
相关资料
更多










