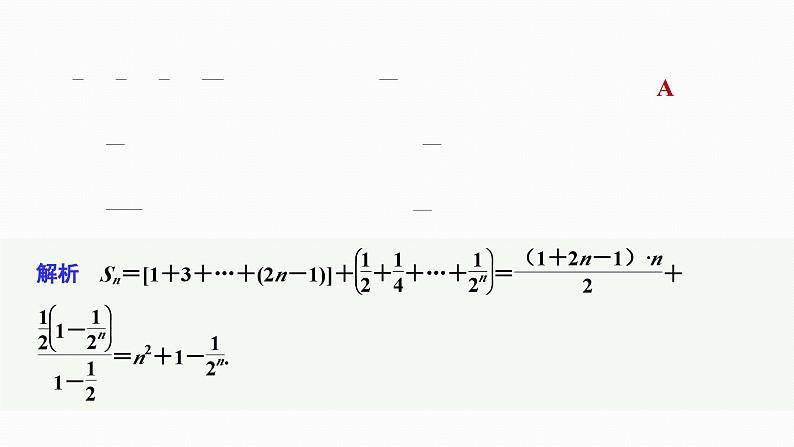
2025高考数学一轮复习-6.4-数列求和【课件】

这是一份2025高考数学一轮复习-6.4-数列求和【课件】，共60页。PPT课件主要包含了知识诊断基础夯实，常用结论，·220－2，an＝2n＋1，考点突破题型剖析，综上所述，当n为奇数时，所以Tn＝，数列中的奇偶项问题，所以an＝2n－1等内容，欢迎下载使用。
ZHISHIZHENDUANJICHUHANGSHI
(2)等比数列的前n项和公式：
1.特殊数列的求和公式(1)等差数列的前n项和公式：
2.数列求和的几种常用方法(1)分组转化法把数列的每一项分成两项或几项，使其转化为几个等差、等比数列，再求解.(2)裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和.(3)错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，这个数列的前n项和可用错位相减法求解.(4)倒序相加法如果一个数列{an}的前n项中与首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前n项和即可用倒序相加法求解.
4.在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解.
解析　(3)要分a＝0或a＝1或a≠0且a≠1讨论求解.
解析　S20＝4·1＋5·21＋6·22＋…＋23·219，2S20＝4·2＋5·22＋6·23＋…＋23·220，
4.(易错题)数列{(n＋3)·2n－1}前20项的和为___________.
故S20＝22·220－2.
解析　由f(x)＋f(1－x)＝4，可得f(0)＋f(1)＝4，…，
所以2an＝(f(0)＋f(1))
KAODIANTUPOTIXINGPOUXI
解　设等差数列{an}的公差为d，因为关于x的不等式a1x2－S2x＋2＜0的解集为(1，2)，
例1 已知等差数列{an}的前n项和为Sn，且关于x的不等式a1x2－S2x＋2＜0的解集为(1，2).(1)求数列{an}的通项公式；
又S2＝2a1＋d，所以a1＝d，
所以数列{an}的通项公式为an＝n.
(2)若数列{bn}满足bn＝a2n＋2an－1，求数列{bn}的前n项和Tn.解　由(1)可得，a2n＝2n，2an＝2n.因为bn＝a2n＋2an－1，所以bn＝2n－1＋2n，所以数列{bn}的前n项和Tn＝(1＋3＋5＋…＋2n－1)＋(2＋22＋23＋…＋2n)
解　Sn＝2(1＋3＋…＋3n－1)＋[－1＋1－1＋…＋(－1)n]·(ln 2－ln 3)＋[－1＋2－3＋…＋(－1)nn]ln 3，所以当n为偶数时，
训练1 已知数列{an}的通项公式是an＝2·3n－1＋(－1)n(ln 2－ln 3)＋(－1)nnln 3，求其前n项和Sn.
例2 给出以下三个条件：①4a3，3a4，2a5成等差数列；②∀n∈N*，点(n，Sn)均在函数y＝2x－a的图象上，其中a为常数；③S3＝7.请从这三个条件中任选一个将下面的题目补充完整，并求解.设{an}是一个公比为q(q＞0，且q≠1)的等比数列，且它的首项a1＝1，________.(1)求数列{an}的通项公式；
解　选①进行作答.因为4a3，3a4，2a5成等差数列，所以6a4＝4a3＋2a5，即6a3·q＝4a3＋2a3q2，解得q＝1(舍)或q＝2，所以an＝2n－1.选②进行作答.由题意得Sn＝2n－a，因为a1＝S1＝2－a＝1，所以a＝1，所以Sn＝2n－1，
当n≥2时，Sn－1＝2n－1－1，则an＝Sn－Sn－1＝2n－1，当n＝1时，a1＝1，符合上式，所以an＝2n－1.选③作答.由S3＝7，得a1＋a2＋a3＝7，即a1＋a1·q＋a1·q2＝7，解得q＝2或q＝－3，又因为q＞0，所以q＝2，所以an＝2n－1.
证明　bn＝2lg22n－1＋1＝2n－1，n∈N*，
解　已知Sn＝2an－a1，当n≥2时，Sn－1＝2an－1－a1，两式相减得an＝2an－1，n≥2，
所以数列{an}是公比为2，首项为1的等比数列，所以{an}的通项公式为an＝2n－1.
解　设{an}的公比为q，则an＝qn－1.因为a1，3a2，9a3成等差数列，
解　选①，即Sn＝2an＋1.①当n＝1时，S1＝2a1＋1，故a1＝－1；当n≥2时，Sn－1＝2an－1＋1，②①②两式相减得an＝2an－1，
所以{an}为等比数列，其中公比为2，首项为－1.所以an＝－2n－1.选②，即a1＝－1，lg2(anan＋1)＝2n－1.所以当n≥2时，lg2(anan＋1)－lg2(an－1an)＝2，
所以{a2k－1}(k∈N*)为等比数列，其中首项为a1＝－1，公比为4，所以a2k－1＝－1×4k－1＝－2(2k－1)－1；由a1＝－1，lg2(a1a2)＝1，得a2＝－2，
同理可得，a2k＝－2×4k－1＝－22k－1(k∈N*).综上，an＝－2n－1.
所以{an}为等比数列，设其公比为q，
又因为{an}为单调数列，所以q＞0，
(2)求数列{－nan}的前n项和Tn.注：如果选择多个条件分别解答，按第一个解答计分.解　由(1)知，－nan＝n·2n－1，所以Tn＝1＋2×2＋3×22＋…＋(n－1)·2n－2＋n·2n－1，2Tn＝2＋2×22＋…＋(n－2)·2n－2＋(n－1)·2n－1＋n·2n，两式相减得－Tn＝1＋2＋22＋…＋2n－2＋2n－1－n·2n＝(2n－1)－n·2n.所以Tn＝(n－1)·2n＋1.
数列中的奇、偶项问题是对一个数列分成两个新数列进行单独研究，利用新数列的特征(等差、等比数列或其他特征)求解原数列.(1)数列中的奇、偶项问题的常见题型①数列中连续两项和或积的问题(an＋an＋1＝f(n)或an·an＋1＝f(n))；②含有(－1)n的类型；③含有{a2n}，{a2n－1}的类型；④已知条件明确奇偶项问题.(2)对于通项公式分奇、偶不同的数列{an}求Sn时，我们可以分别求出奇数项的和与偶数项的和，也可以把a2k－1＋a2k看作一项，求出S2k，再求S2k－1＝S2k－a2k.
解　依题意可知数列{an＋1－an}是以a2－a1＝3－1＝2为首项，以2为公比的等比数列，所以an＋1－an＝2×2n－1＝2n，等式两边同时除以2n得，
例1 已知数列{an}中，a1＝1，a2＝3，且数列{an＋1－an}是以2为公比的等比数列.(1)求数列{an}的通项公式；
一、含有(－1)n的类型
(2)令cn＝(－1)n＋1an，求数列{cn}的前n项和Sn.解　由(1)得，cn＝(－1)n＋1(2n－1)，当n为偶数时，Sn＝(21－1)－(22－1)＋(23－1)－(24－1)＋…＋(2n－1－1)－(2n－1)＝21－22＋23－24＋…＋2n－1－2n
当n为奇数时，n－1为偶数，
解　法一　当n为偶数时，Sn＝a1＋a2＋…＋an＝(a1＋a3＋…＋an－1)＋(a2＋a4＋…＋an)＝(1＋3＋…＋n－1)
二、已知条件明确的奇偶项问题
∴S2n＝a1＋a2＋…＋a2n＝(a1＋a3＋…＋a2n－1)＋(a2＋a4＋…＋a2n)＝(1＋3＋…＋2n－1)＋
放缩法的注意事项以及解题策略：(1)对于“和式”数列不等式，若能够直接求和，则考虑先求和，再放缩证明不等式；若不能或很难求和，则可考虑先放缩后求和证明不等式.而对于“和式”数列不等式，放缩的最主要目的是通过放缩，把原数列变为可求和、易求和的数列.(2)明确放缩的方向：是放大还是缩小.若要证明小于某值，则放大；若要证明大于某值，则缩小.(3)放缩的项数：不一定对所有项进行放缩，有时从第一项开始，或从第二项，或从第三项等开始.
(4)常见的放缩方法有：①增加(减少)某些项；②增大(减少)分子(分母)；③增大(减小)被开方数；增大(减小)底数(指数)；④利用不等式的性质或基本不等式；⑤利用函数的单调性等.放缩法，常见的放缩技巧有：
解　设等差数列{an}的公差为d，
例1 已知Sn为等差数列{an}的前n项和，S4＝24，S10＝120.(1)求Sn；
得a1＝3，d＝2.∴Sn＝3n＋n2－n＝n2＋2n.
又S1＝a1＝1，所以a2＝4.
整理得(n＋1)an＝nan＋1－n(n＋1)，
(2)求数列{an}的通项公式；
故数列{an}的通项公式为an＝n2.
综上，对一切正整数n，
FENCENGXUNLIAN GONGGUTISHENG
解析　S100＝(－1＋3)＋(－5＋7)＋…＋(－197＋199)＝2×50＝100.
1.数列{an}的通项公式是an＝(－1)n(2n－1)，则该数列的前100项之和为(　　)A.－200 B.－100 C.200 D.100
解析　由题意知{an}是以2为公差的等差数列，又a1＝－5，所以|a1|＋|a2|＋…＋|a6|＝|－5|＋|－3|＋|－1|＋1＋3＋5＝5＋3＋1＋1＋3＋5＝18.
2.已知数列{an}满足an＋1－an＝2，a1＝－5，则|a1|＋|a2|＋…＋|a6|＝(　　)A.9 B.15 C.18 D.30
3.我国古代数学名著《算法统宗》中说：“九百九十六斤棉，赠分八子做盘缠.次第每人多十七，要将第八数来言.务要分明依次第，孝和休惹外人传.”意为：“996斤棉花，分别赠送给8个子女做旅费，从第1个孩子开始，以后每人依次多17斤，直到第8个孩子为止.分配时一定要按照次序分，要顺从父母，兄弟间和气，不要引得外人说闲话.”在这个问题中，第8个孩子分到的棉花为(　　)A.184斤 B.176斤C.65斤 D.60斤
解析　依题意得，八个子女所得棉花斤数依次构成等差数列，设该等差数列为{an}，公差为d，前n项和为Sn，第一个孩子所得棉花斤数为a1，
解得a1＝65，∴a8＝a1＋(8－1)d＝184.
解析　由an＋2＝an＋1－an＝(an－an－1)－an＝－an－1＝－(an－2－an－3)＝－(an－3－an－4)＋an－3＝an－4，得{an}是周期为6的周期函数，又a3＝a2－a1＝3－1＝2，a4＝2－3＝－1，a5＝－1－2＝－3，a6＝－3＋1＝－2，∵100＝16×6＋4，∴S100＝16×(1＋3＋2－1－3－2)＋(1＋3＋2－1)＝5.
4.在数列{an}中，若a1＝1，a2＝3，an＋2＝an＋1－an(n∈N*)，则该数列的前100项之和是(　　)A.18 B.8 C.5 D.2
解析　设f(x)＝xα，且f(x)过点(4，2)，
∴数列{bn}的前n项和Sn＝b1＋b2＋b3＋…＋bn＝
所以{an}的奇数项和偶数项均为公比为2的等比数列，
7.已知数列{an}的首项为－1，anan＋1＝－2n，则数列{an}的前10项之和等于________.
∴S10＝(a1＋a3＋…＋a9)＋(a2＋a4＋…＋a10)
解析　S2 021＝a1＋(a2＋a3)＋(a4＋a5)＋…＋(a2 020＋a2 021)，又an＋1＋an＝n－1 009(n∈N*), 且a1＝1，∴S2 021＝1＋(2－1 009)＋(4－1 009)＋…＋(2 020－1 009)＝1＋(2＋4＋6＋…＋2 020)－1 009×1 010
8.已知数列{an}满足a1＝1，且an＋1＋an＝n－1 009(n∈N*)，则其前2 021项之和S2 021＝________.
解析　Sn＝1×21＋2×22＋…＋n×2n，则2Sn＝1×22＋2×23＋…＋n×2n＋1，两式相减得
9.已知数列{nan}的前n项和为Sn，且an＝2n，且使得Sn－nan＋1＋50