初中数学青岛版九年级上册2.4 解直角三角形试讲课课件ppt

这是一份初中数学青岛版九年级上册2.4 解直角三角形试讲课课件ppt，共22页。PPT课件主要包含了课堂导入，探究新知，解直角三角形的定义，知识点1，∠A的度数，tanB，课堂练习等内容，欢迎下载使用。

学习目标：1.知道解直角三角形的概念，理解直角三角形中除直角以外的五个元素之间的关系.2.能综合运用勾股定理、直角三角形的两个锐角互余及锐角三角比解直角三角形.
重点：能综合运用勾股定理、直角三角形的两个锐角互余及锐角三角比解直角三角形.
难点：正确利用锐角三角比解直角三角形.
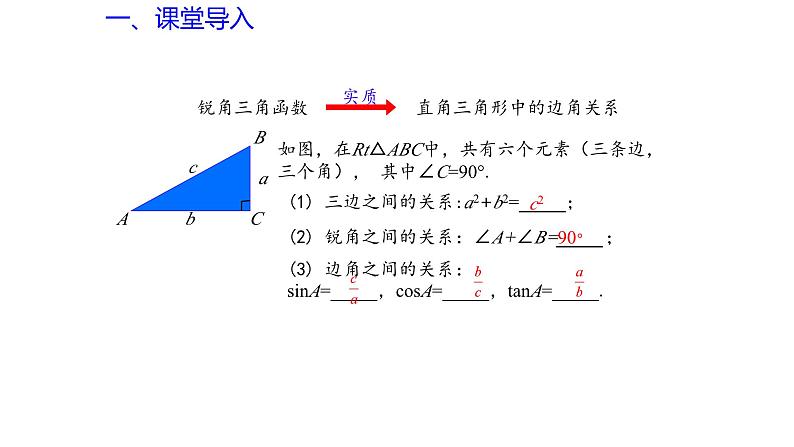
直角三角形中的边角关系
如图，在Rt△ABC中，共有六个元素（三条边，三个角）， 其中∠C=90°.
(1) 三边之间的关系:a2+b2=_____；
(2) 锐角之间的关系：∠A+∠B=_____；
(3) 边角之间的关系：sinA=_____，csA=_____，tanA=_____.
如图是意大利的比萨斜塔，设塔顶中心点为B，塔身中心线与垂直中心线的交点为A ，过B点向垂直中心线引垂线，垂足为C，在Rt△ABC中，∠C=90°，BC=5.2米，AB=54.5米.
知道以上条件，你能求出∠A的度数吗？
Rt△ABC中，∠C=90°， BC=5.2 m，AB=54.5 m.
利用计算器可得∠A ≈ 5°28′.
　　一般地，直角三角形中，除直角外，共有五个元素，即三条边和两个锐角.由直角三角形中已知元素，求出其余未知元素的过程，叫做解直角三角形.
以上问题抽象为数学问题即为：已知直角三角形的斜边和一条直角边，求它的锐角的度数.
在Rt△ABC中，如果已知其中两边的长，你能求出这个三角形的其他元 素吗？
类型1 已知两边解直角三角形
勾股定理或者csB或者sinA求BC
练习： 已知在Rt△ABC中，∠C＝90°，∠A，∠B，∠C 的对边分别为a，b，c，且c＝5，b＝4，求这个三角 形的其他元素．(角度精确到1′) 求这个直角三角形的其他元素，与“解这个直角三角 形”的含义相同．求角时，可以先求∠A，也可以先 求∠B，因为 ＝sin B＝cs A.
由c＝5，b＝4，得sin B＝ ＝0.8，∴∠B≈53°8′.∴∠A＝90°－∠B≈36°52′.由勾股定理得
应用勾股定理求斜边，应用角的正切值求出一锐角，再利用直角三角形的两锐角互余，求出另一锐角．一般不用正弦或余弦值求锐角，因为斜边是一个中间量，如果是近似值，会影响结果的精确度．
已知斜边和直角边：先利用勾股定理求出另一直角边，再求一锐角的正弦和余弦值，即可求出一锐角，再利用直角三角形的两锐角互余，求出另一锐角．
已知直角三角形的一边和一锐角，解直角三角形时，若已知一直角边a和一锐角A： ① ∠B=90 °- ∠ A；②c= 若已知斜边c和一个锐角A： ① ∠ B=90°- ∠ A；②a=c·sin A ; ③b=c·cs A.
类型2 已知一边及一锐角解直角三角形
例题2 如图，在 Rt△ABC中，∠C=90°，∠B=35°，b=20，解这个直角三角形（结果保留小数点后一位）．
直角边a、斜边c、锐角A.
练习 如图，在Rt△ABC中∠C=90°，∠A=30°，a=5，求∠B，b，c.
解： ∠B=900-∠A= 900-300=600
由直角三角形中已知的元素求出未知元素的过程，叫作解直角三角形.
两边：两直角边或斜边、一直角边
一边一角：直角边、一锐角或斜边、一锐角
1.必做作业： ①课本P52复习与巩固1-4 ②预习2.4;2.选做作业： 拓展与延伸7