





青岛版九年级上册2.5 解直角三角形的应用优秀ppt课件
展开学习目标:1.学生会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决.2.逐步培养学生分析问题、解决问题的能力.3.渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识。
重点:能运用解直角三角形知识解决坡度、坡比有关的实际问题.
难点:在解题过程中体会数形结合、转化的数学思想,并从这些问题中归纳出解题的思路方法.
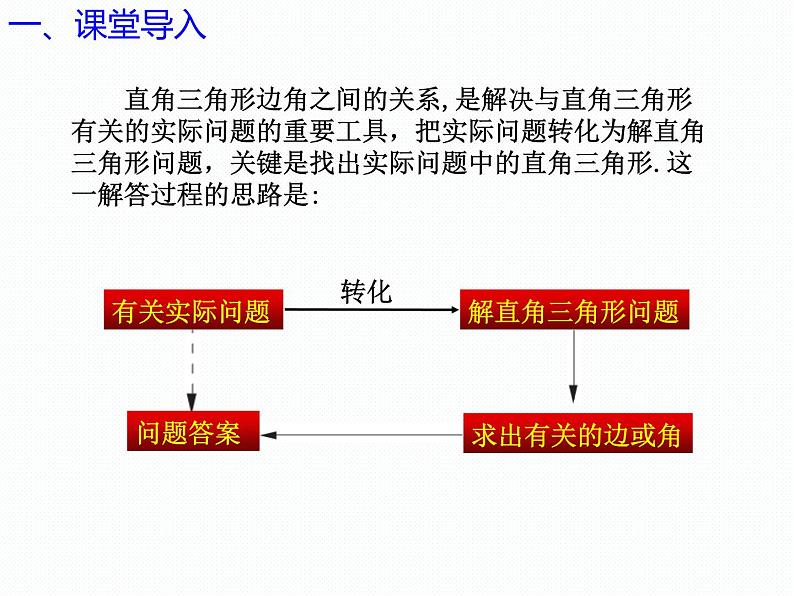
直角三角形边角之间的关系,是解决与直角三角形有关的实际问题的重要工具,把实际问题转化为解直角三角形问题,关键是找出实际问题中的直角三角形.这一解答过程的思路是:
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝或山的高度h时,我们无法直接测量,我们又该如何呢?
图1中只要测量出坡角α的度数和坡面l的长度
化整为零,积零为整,化曲为直,以直代曲是解决这类问题的基本策略,也是今后数学学习中的重要思想。
与测量坝高相比,测山的难度在于:坝坡是“直”的,而山坡是“曲”的,怎么解决这样的问题呢?
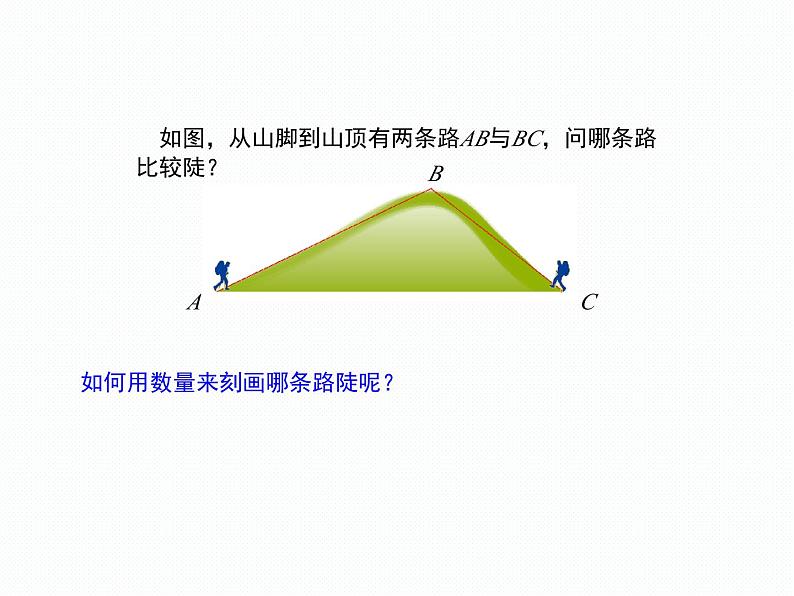
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
例 某地计划在河流的上游修建一条拦水大坝.大坝的横断面ABCD是梯形(如图),坝顶宽BC=6 m,坝高23m,迎水坡AB的坡度i=1∶3,背水坡CD的坡度i=1∶2.5.求:(1) 斜坡CD的坡角α (精确到 1°);
解: 斜坡CD的坡度i = tanα = 1 : 2.5=0.4,由计算器可算得α≈22°.故斜坡CD的坡角α 为22°.
解:分别过点B、C作BE⊥AD,CF⊥AD,垂足分别为点E、 F,由题意可知BE=CF=23m , EF=BC=6m.
(2) 坝底AD与斜坡AB的长度 (精确到0.1m).
解题关键:适当添加辅助线,构造直角三角形
例 水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求:
在Rt△ABE中,由勾股定理可得
故坝底AD的长度为132.5m,斜坡AB的长度为72.7m.
练习1.如图,完成下列填空:
(2)斜坡的坡角是45°,则坡比是 ;
(3)斜坡长是12米,坡高6米,则坡比是 ;
练习2.如图,防洪大堤的横截面是梯形 ABCD,其中AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20m,求改造后的坡长AE.(结果保留根号)
解:过点A作AF⊥BC于点F,在Rt△ABF中,∵∠ABF =∠α=60°,AB=20m
又∵∠E=∠β=45°
3.如图,一山坡的坡度为i=1:2.小刚从山脚A出发,沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
4.如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m)
初中数学青岛版八年级上册1.3 尺规作图精品ppt课件: 这是一份初中数学青岛版八年级上册<a href="/sx/tb_c92978_t3/?tag_id=26" target="_blank">1.3 尺规作图精品ppt课件</a>,共16页。PPT课件主要包含了第一章全等三角形,青岛版八年级数学上册,第二课时,学习目标,实验与探究,图1-28,确定三个顶点的位置,成果展示,图1-29,①作∠B∠α等内容,欢迎下载使用。
青岛版八年级上册1.3 尺规作图完美版课件ppt: 这是一份青岛版八年级上册<a href="/sx/tb_c92978_t3/?tag_id=26" target="_blank">1.3 尺规作图完美版课件ppt</a>,共16页。PPT课件主要包含了3cm,第一章全等三角形,青岛版八年级数学上册,第一课时,学习目标,交流与发现,无刻度的直尺,作过任意一点的直线,连接两个点作一条线段,经过两点作一条直线等内容,欢迎下载使用。
数学2.5 解直角三角形的应用精品课件ppt: 这是一份数学<a href="/sx/tb_c99061_t3/?tag_id=26" target="_blank">2.5 解直角三角形的应用精品课件ppt</a>,共21页。PPT课件主要包含了2边之间的关系,1角之间的关系,两条边或一边一角,温故知新,转化思想,情境导入,能力拔高,课堂小结等内容,欢迎下载使用。














