




数学2.5 解直角三角形的应用精品课件ppt
展开∠A + ∠B = 90 °;
勾股定理:a2+b2=c2 ;
(3)角与边之间的关系:
2. 如果知道直角三角形的几个元素就可以求其 他的元素?有几种情况?
两个元素(至少一个是边)
1.直角三角形的边角关系:
当三角形不是直角三角形时,作一边上的高,把斜三角形转化为直角三角形,把问题转化为解直角三角形. 化“未知”为“已知”.
有一位小朋友,正抬头仰望高高飘扬的五星红旗,这时她陷入了沉思:我怎样才能测出旗杆的高度?
如果给你足够的工具,聪明的你会用所学知识测出旗杆的高度吗?
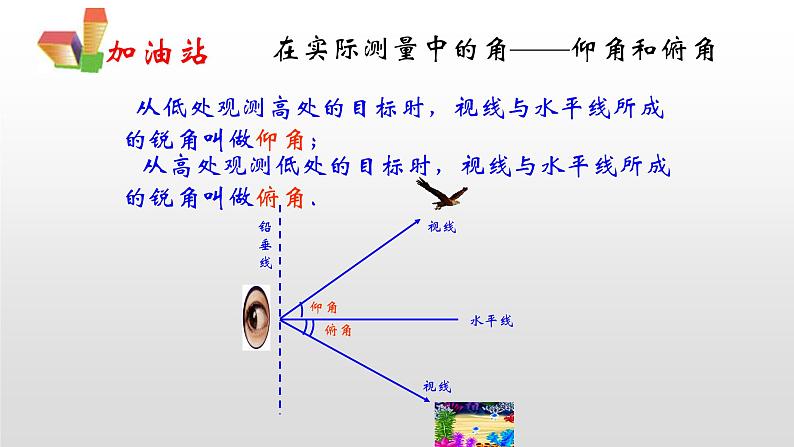
在实际测量中的角——仰角和俯角
从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.
从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;
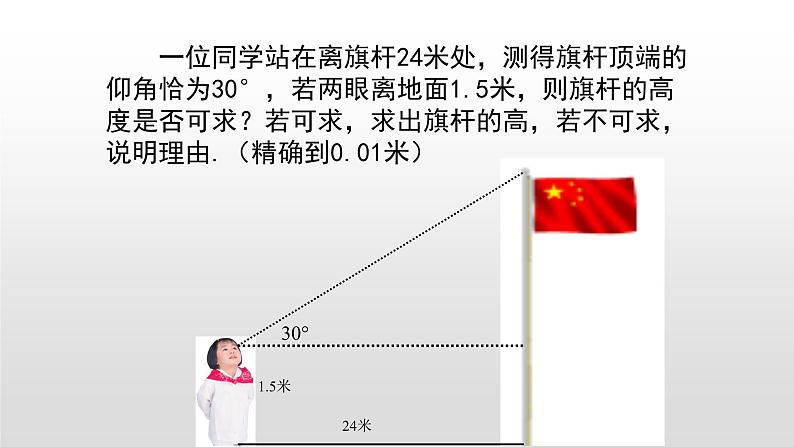
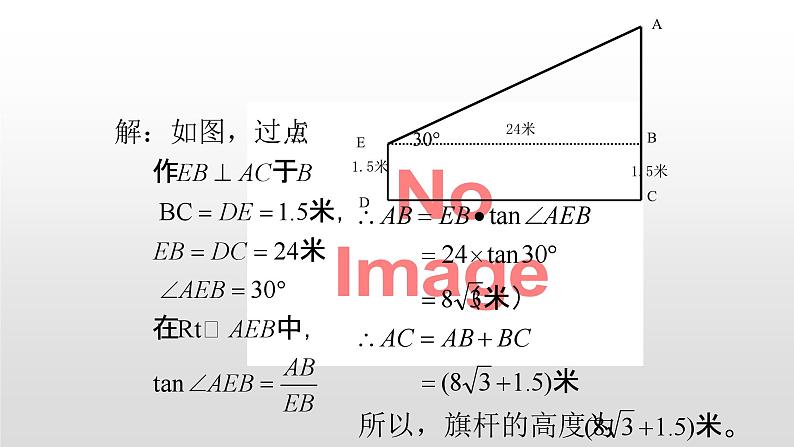
一位同学站在离旗杆24米处,测得旗杆顶端的仰角恰为30°,若两眼离地面1.5米,则旗杆的高度是否可求?若可求,求出旗杆的高,若不可求,说明理由.(精确到0.01米)
例1 如图,某直升飞机执行海上搜救任务,在空中A 处观测到海面上有一目标B ,这时飞机的高度为1.5 km,飞机A距目标B的距离是4.5km,求飞机在A处观测目标B的俯角α. (sin19°≈0.333,tan19°≈0.3457)
解:由题意得AC=1.5 km,AB=4.5km,∠C=90°
例2、如图,为了测量某建筑物BC的高度, 在A处测得建筑物顶端C的仰角为30°, 沿AC方向前进12m到达点D处,在D处 测得建筑物顶端B的仰角为45° 求:建筑物BC的高度。
例3、如图,物化大厦离小强家60m,小强 从自家的窗中眺望大厦,并测得大厦顶部 的仰角为45°,而大厦底部的俯角为30°. 求:该大厦的高度。
例4、如图,平地上一棵树高为5米,两次观察地面上的影子,第一次是阳光与地面成45°时,第二次是阳光与地面成30°时,求第二次观察到的影子比第一次长多少米?
练习1 .如图,在电线杆上离地面6 米处用拉线固定电线杆,拉线和地面之间的夹角为60° , 求拉线AC 的长和拉线下端点A 与线杆底部D 的距离(精确到0 . 1 米).
2.如图,一架梯子斜靠在墙上,梯子顶端到地面的距离BC = 3.2 米,底端到墙根的距离AC = 2.4 米. (1)求梯子的长度和梯子与地面所成角的大小(精确到1 ' ) ; (2) 如果把梯子的底端到墙角的距离减少0 . 4 米,那么梯子与地面所成的角是多少?
2.解决实际问题的思路是:
从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.
1. 从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;
必做题:课本P83A组 1、2、8题选做题:课本P83A组 3题
初中数学青岛版八年级上册1.3 尺规作图精品ppt课件: 这是一份初中数学青岛版八年级上册<a href="/sx/tb_c92978_t3/?tag_id=26" target="_blank">1.3 尺规作图精品ppt课件</a>,共16页。PPT课件主要包含了第一章全等三角形,青岛版八年级数学上册,第二课时,学习目标,实验与探究,图1-28,确定三个顶点的位置,成果展示,图1-29,①作∠B∠α等内容,欢迎下载使用。
青岛版八年级上册1.3 尺规作图完美版课件ppt: 这是一份青岛版八年级上册<a href="/sx/tb_c92978_t3/?tag_id=26" target="_blank">1.3 尺规作图完美版课件ppt</a>,共16页。PPT课件主要包含了3cm,第一章全等三角形,青岛版八年级数学上册,第一课时,学习目标,交流与发现,无刻度的直尺,作过任意一点的直线,连接两个点作一条线段,经过两点作一条直线等内容,欢迎下载使用。
青岛版九年级上册2.5 解直角三角形的应用优秀ppt课件: 这是一份青岛版九年级上册<a href="/sx/tb_c99061_t3/?tag_id=26" target="_blank">2.5 解直角三角形的应用优秀ppt课件</a>,共17页。PPT课件主要包含了有关实际问题,解直角三角形问题,求出有关的边或角,问题答案,课堂导入,探究新知,课堂练习等内容,欢迎下载使用。














