



青岛版九年级上册3.1 圆的对称性精品第1课时课后练习题
展开题型一 利用垂径定理求值
1.如图,是的直径,是弦,,垂足为M,则下列结论中错误的是( )
A. B.C. D.
【答案】C
【分析】垂直于弦的的直径平分弦及弦所对的两条弧,根据垂径定理即可进行判断,熟练掌握垂径定理的内容是解题的关键.
【详解】解:∵是的直径,是弦,,垂足为M,
∴,,,
无法判断,
故选:C
2.下列语句,错误的是( )
A.直径是弦B.过圆心的弦是直径
C.平分弧的直径垂直于弧所对的弦D.相等的圆心角所对的弧相等
【答案】D
【分析】考查了圆周角定理、垂径定理以及弦弧的概念等知识.根据弦的定义、垂径定理的推论、圆周角定理,即可求得答案.
【详解】A. 直径是弦,故该选项正确,不符合题意;
B. 过圆心的弦是直径,故该选项正确,不符合题意;
C. 平分弧的直径垂直于弧所对的弦,故该选项正确,不符合题意;
D. 在同圆或等圆中,相等的圆心角所对的弧相等,故该选项不正确,符合题意;
故选:D.
3.下列说法正确的是( )
A.垂直于弦的直线平分弦所对的两条弧B.平分弦的直径垂直于弦
C.垂直于直径的直线平分这条直径D.弦的垂直平分线经过圆心
【答案】D
【分析】根据垂径定理对选项A、C进行判断,根据垂径定理的推论对B、D选项进行判断.
【详解】解:A.垂直于弦的直径平分弦所对的两条弧,所以A选项错误;
B.平分弦(非直径)的直径垂直于弦,所以B选项错误;
C.垂直于直径的弦被这条直径平分,所以C选项错误;
D.弦的垂直平分线经过圆心,所以D选项正确.
故选:D.
【点睛】本题考查垂径定理及垂径定理的推论,掌握并理解定理的内容是解答此题的关键
4.如图,是的直径,弦于点E,,,则( )
A.6B.C.9D.12
【答案】C
【分析】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
先根据垂径定理得到,然后利用勾股定理可计算出的长.
【详解】解:,
,
在中,.
故选:C.
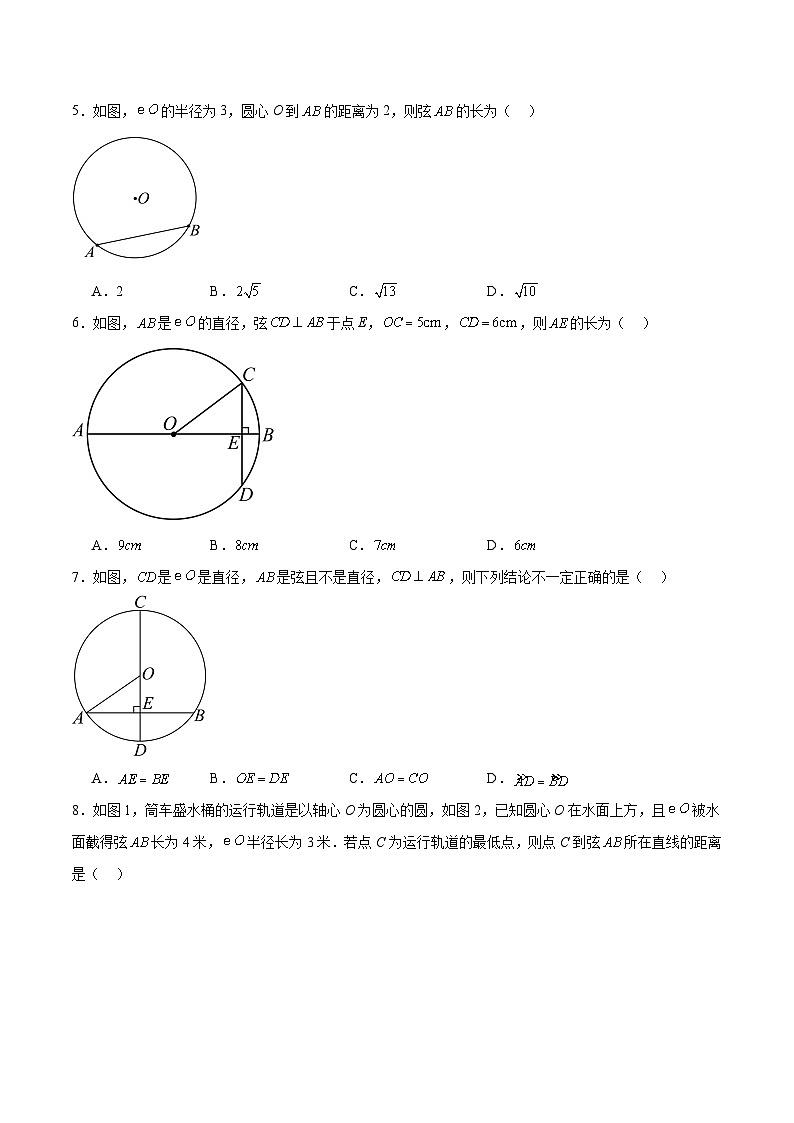
5.如图,的半径为3,圆心O到的距离为2,则弦的长为( )
A.2B.C.D.
【答案】B
【分析】本题考查了垂径定理和勾股定理,能熟记垂径定理是解此题的关键.连接半径,构造直角三角形,利用勾股定理求出的长,从而求出的长.
【详解】解:连接,过O点作于C,如图,
于C,
,
在中,,,
,
.
故选:B.
6.如图,是的直径,弦于点E,,,则的长为( )
A.B.C.D.
【答案】A
【分析】本题考查垂径定理,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.根据垂径定理推出,再利用勾股定理求出即可解决问题.
【详解】解:,是直径,,
,
在中,(),
(),
故选:.
7.如图,是是直径,是弦且不是直径,,则下列结论不一定正确的是( )
A.B.C.D.
【答案】B
【分析】由于, 根据垂径定理有, , 不能得出, 圆的半径都相等.
【详解】解:如图所示,
∵,
∴, ,
的半径都相等,那么
,
不能得出.
故选:.
【点睛】本题考查了垂径定理.解题的关键是熟练掌握垂径定理的内容.
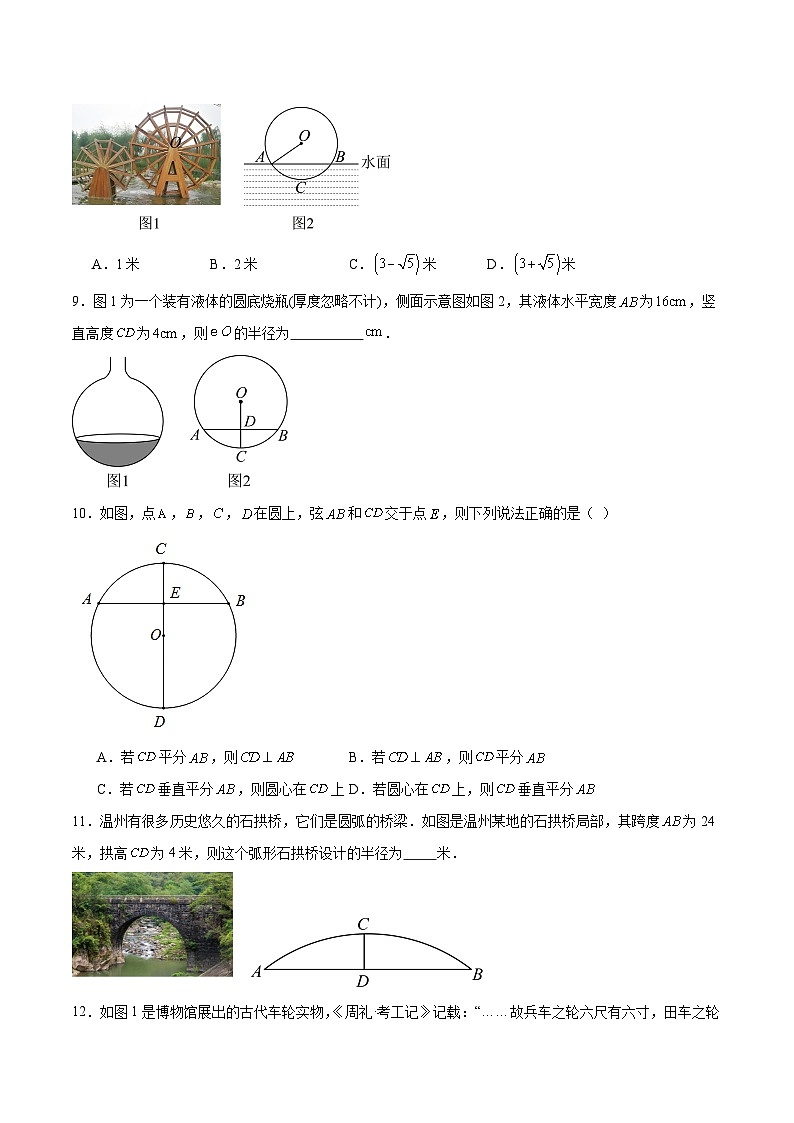
8.如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且被水面截得弦长为4米,半径长为3米.若点C为运行轨道的最低点,则点C到弦所在直线的距离是( )
A.1米B.2米C.米D.米
【答案】C
【分析】本题考查了垂径定理和勾股定理的应用,熟练掌握垂径定理和勾股定理是解题的关键.
连接,交于D,由垂径定理得(米),再由勾股定理得(米),然后求出的长即可.
【详解】连接,交于D,
由题意得:米,,
米,,
在中
米,
米,
即点C到弦所在直线的距离是米,
故选:C.
9.图1为一个装有液体的圆底烧瓶(厚度忽略不计),侧面示意图如图2,其液体水平宽度为,竖直高度为,则的半径为 .
【答案】10
【分析】本题考查垂径定理,勾股定理.
由垂径定理得到,设的半径为,则,,在中,根据勾股定理有,代入即可解答.
【详解】解:连接,
∵,
∴,
设的半径为,则,
∴,
∵在中,,
即,
解得:,
∴的半径为.
故答案为:10.
10.如图,点,,,在圆上,弦和交于点,则下列说法正确的是( )
A.若平分,则B.若,则平分
C.若垂直平分,则圆心在上D.若圆心在上,则垂直平分
【答案】C
【分析】根据垂径定理的内容和垂径定理的推论的内容进行判断.
【详解】解:A、平分弦(不是直径)的直径垂直于弦,原说法错误,不符合题意;
B、垂直于弦的直径平分弦,原说法错误,不符合题意;
C、弦的垂直平分线必经过圆心,原说法正确,符合题意;
D、若也是直径,则原说法不符合题意;
故选:C.
【点睛】本题考查了垂径定理以及推论,解答时熟悉垂径定理的内容以及推论的内容是关键.
11.温州有很多历史悠久的石拱桥,它们是圆弧的桥梁.如图是温州某地的石拱桥局部,其跨度为24米,拱高为4米,则这个弧形石拱桥设计的半径为 米.
【答案】20
【分析】本题考查了垂径定理、勾股定理,找出石拱桥圆弧形的圆心,连接,设半径为米,则米,由垂径定理可得米,再由勾股定理计算即可得出答案.
【详解】解:如图,找出石拱桥圆弧形的圆心,连接,
,
设半径为米,则米,
∵跨度为24米,,
∴米,
由勾股定理得:,
∴,
解得:,
∴这个弧形石拱桥设计的半径为米,
故答案为:.
12.如图1是博物馆展出的古代车轮实物,《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸……”据此,我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A,B两点,设所在圆的圆心为O,半径为.
作弦AB的垂线OC,D为垂足,则___________.
经测量,,则___________;用含r的代数式表示___________.
在中,由勾股定理可列出关于r的方程:___________.解得.
通过换算,车轮直径约为六尺六寸,可验证此车轮为___________之轮.(填“兵车”或“田车”)
【答案】,,,,兵车
【分析】根据垂径定理,进行作答即可.
【详解】解:根据垂直弦的直径平分弦可知:,
∵,
∴,,
∴,
解得:,
∴此车轮为:兵车之轮;
故答案为:,,,,兵车.
【点睛】本题考查垂径定理.熟练掌握:垂直于弦的直径,平分弦,是解题的关键.
13.如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB,垂足为E,已知CD=6,AE=1,求⊙O的半径.
【答案】
【分析】连接,由垂径定理可得,,设半径为,由勾股定理列方程求解即可.
【详解】解:连接,如下图:
∵AB是⊙O的直径,CD⊥AB
∴
设半径为,则
由勾股定理得:,即
解得
⊙O的半径为
【点睛】此题考查了垂径定理以及勾股定理解直角三角形,解题的关键是熟练掌握相关基本性质.
14.如图,排水管截面的半径为5分米,水面宽6分米,,求水的最大深度.
【答案】1分米
【分析】本题考查对垂径定理和勾股定理的熟练掌握以及对其在实际生活中的应用,要求会根据所给条件求出某一直角边或斜边.关键在于直角三角形的创造及对题意水最大深度的实际求解.
【详解】解:连接,
∵,
∴为直角三角形,
∵排水管截面的半径为5分米,
∴,,
∵水面宽6分米,,
∴
在中,,
∴.
15.如图,是一个高速公路的隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面米,拱高米,求圆的半径.
【答案】圆的半径为米.
【分析】本题考查垂径定理和勾股定理,利用垂径定理求出的长,设米,得到米,再利用勾股定理建立方程即可求解.
【详解】解:连接,
有,
路面米,
米,
设米,
拱高米,
米,
,
,
解得,
圆的半径为米.
16.如图,为的直径,弦于点E,若,,求弦的长.
【答案】.
【分析】本题主要考查了垂径定理,勾股定理等,连接,根据垂径定理得到,根据求出、的长,根据求出的长,利用勾股定理求出,即可得到的长.
【详解】解:连接,如图所示:
∵为的直径,,
∴,,
∴,
在中,由勾股定理得:,
∴.
17.如图,两个同心圆的半径分别为15和12,大圆的一条弦有一半在小圆内,则这条弦落在小圆内部分的弦长等于( )
A.B.C.D.
【答案】D
【分析】本题考查的是垂径定理的应用,先画出图形,再利用垂径定理与勾股定理计算即可.
【详解】解:如图,记弦与圆的交点分别为,连接,
过作于,
∴,,
∵大圆的一条弦有一半在小圆内,
∴,
∴,
∴,
∴,
∴,
解得:,
∴.
故选:D
18.⊙O的半径是10,弦,,则弦与的距离是( )
A.2B.14C.2或14D.7或1
【答案】C
【分析】本题考查了垂径定理的应用.作于E,于F,由垂径定理得,由于,易得E、O、F三点共线,在和中,利用勾股定理分别计算出与,然后讨论:当圆心O在弦与之间时,与的距离;当圆心O在弦与的外部时,与的距离.
【详解】解:如图,作于E,于F,连,
则,
∵,
∴E、O、F三点共线,
在中,,
在中,,
当圆心O在弦与之间时,与的距离;
当圆心O在弦与的外部时,与的距离.
所以与的距离是14或2.
故选:C.
19.如图,直径与弦交于点E,点F是的中点,延长交于点G,若,且,则的长度是( )
A.4B.C.D.
【答案】C
【分析】此题考查了垂径定理、解直角三角形等知识,求出,,即可得到的长度.
【详解】解:∵点F是的中点,延长交于点G,
∴,
∵,
∴,,
∴,,
∵,
∴
∴
故选:C
20.如图,将一装有水的球形容器放在水平地面上,其轴截面为的一部分,为容器口,为水面,已知半径为,将容器从甲处与地面平行时向右缓慢滚至乙处水面正好经过点B时(水无溢出),点A相对甲处时升高了多少厘米?( )
A.B.C.D.1
【答案】B
【分析】如图甲中,过点O作于点M,交于点N.在图乙中,过点A作于点G,过点O作于点H.交于点J,作于点N.利用勾股定理求出,,证明,进而证明,即可求解.
【详解】解:如图甲中,过点O作于点M,交于点N.在图乙中,过点A作于点G,过点O作于点H.交于点J,作于点N.
如图甲中,∵,
∴,
∴,
∴,,
∴,
∴点A到水面的距离为,
如图乙中,同法可得,
在和中,,
∴,
∴,
∴,
设,则有,
解得,
∴,
∵,
∴,
∴,
∴,
∴此时点A到水平面的距离为,
∴点A相对甲处时升高了.
故选:B.
【点睛】本题主要考查圆的相关知识,涉及垂径定理、勾股定理、全等三角形的判定与性质、相似三角形的判定与性质,解题的关键是作出辅助线构造全等与相似三角形.
21.的半径为13cm,AB、CD是的两条弦,,AB=24cm,CD=10cm,求AB和CD之间的距离.
【答案】7cm或17cm.
【分析】分两种情况进行讨论:①弦AB和CD在圆心同侧;②弦AB和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
【详解】解:①当弦AB和CD在圆心同侧时,如图1
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12−5=7cm;
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴AB与CD之间的距离为7cm或17cm.
【点睛】本题考查了勾股定理和垂径定理的应用,正确作出辅助线、灵活运用定理是解题的关键,注意掌握数形结合思想与分类讨论思想的应用.
数学八年级上册3.6 比和比例优秀第1课时测试题: 这是一份数学八年级上册<a href="/sx/tb_c75254_t7/?tag_id=28" target="_blank">3.6 比和比例优秀第1课时测试题</a>,共2页。试卷主要包含了时代中学的校园中有两块草坪,5︰4,4cmD.4cm等内容,欢迎下载使用。
数学青岛版第3章 对圆的进一步认识3.1 圆的对称性优秀第2课时当堂达标检测题: 这是一份数学青岛版<a href="/sx/tb_c75358_t7/?tag_id=28" target="_blank">第3章 对圆的进一步认识3.1 圆的对称性优秀第2课时当堂达标检测题</a>,文件包含31圆的对称性第2课时分层作业原卷版docx、31圆的对称性第2课时分层作业解析版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
初中数学青岛版九年级上册2.5 解直角三角形的应用精品第1课时当堂检测题: 这是一份初中数学青岛版九年级上册<a href="/sx/tb_c99061_t7/?tag_id=28" target="_blank">2.5 解直角三角形的应用精品第1课时当堂检测题</a>,文件包含25解直角三角形的应用第1课时仰俯角分层作业原卷版docx、25解直角三角形的应用第1课时仰俯角分层作业解析版docx等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。














