云南省迪庆藏族自治州2023-2024学年八年级下学期期末数学试卷(含答案)

这是一份云南省迪庆藏族自治州2023-2024学年八年级下学期期末数学试卷(含答案)，共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列二次根式中,是最简二次根式的是( )
A.B.C.D.
2．在正比例函数的图象上的点是( )
A.B.C.D.
3．下列化简中,正确的是( )
A.B.
C.D.
4．下列各组线段中,不能围成直角三角形的一组是( )
A.,,1B.3,4,5C.6,8,10D.,,
5．下列函数中,y是x的正比例函数的是( )
A.B.C.D.
6．下表记录了甲、乙、丙、丁四个科技创新小组最近几次选拔赛成绩的平均数和方差,如果要选出一个成绩较好且状态稳定的小组去参赛,那么应选的小组是( )
A.甲B.乙C.丙D.丁
7．若最简二次根式能与合并,则m的值为( )
A.0B.1C.2D.3
8．如图,中,的平分线交于E,,,则的长( )
A.1B.1.5C.2D.3
9．若点,点,都在一次函数的图象上,则与的大小关系是( )
A.B.C.D.不能确定
10．在复习特殊的平行四边形时,某小组同学画出了如下关系图,组内一名同学在箭头处填写了它们之间转换的条件,其中填写错误的是( )
A.③有一组邻边相等B.②对角线互相垂直
C.④有一个角是直角D.①一条对角线与其中一边相等
11．如图,在平行四边形中,对角线,相交于点O,.若点E,F分别为,的中点,连接,,,则四边形的周长为( )
A.B.C.40D.24
12．如图,直线与直线相交于点,则方程组的解是( )
A.B.
C.D.
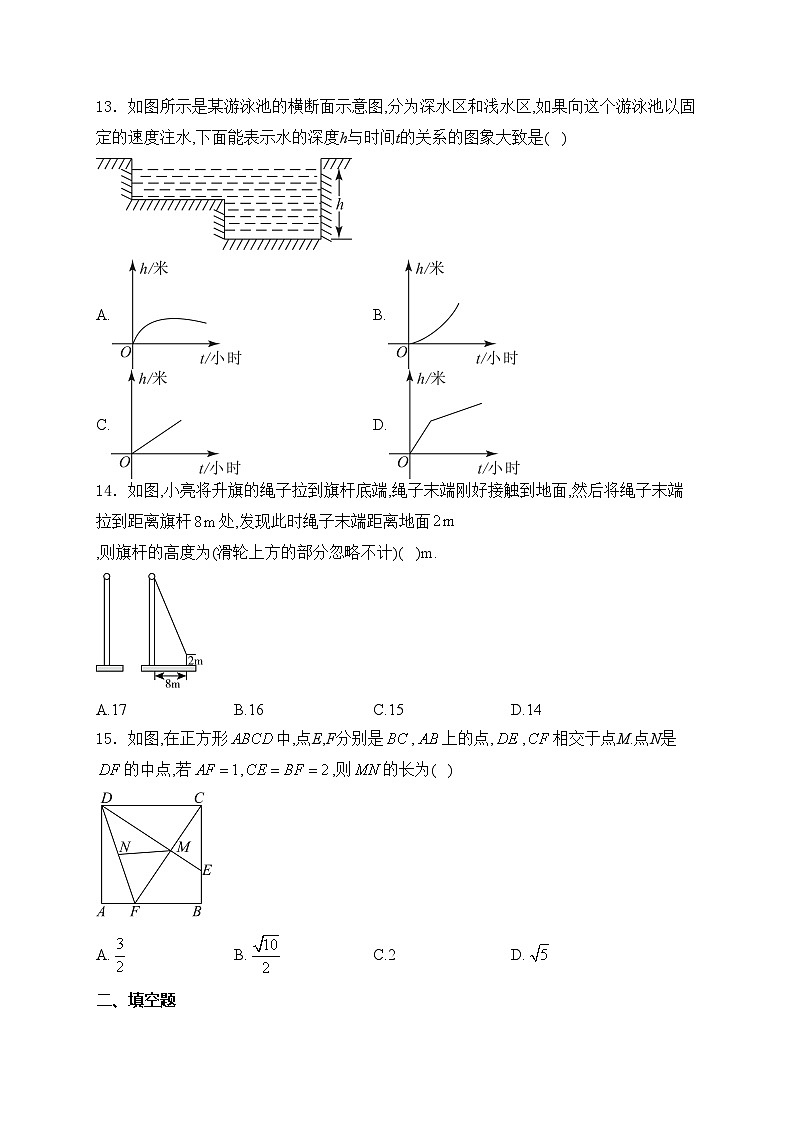
13．如图所示是某游泳池的横断面示意图,分为深水区和浅水区,如果向这个游泳池以固定的速度注水,下面能表示水的深度h与时间t的关系的图象大致是( )
A.B.
C.D.
14．如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆处,发现此时绳子末端距离地面,则旗杆的高度为(滑轮上方的部分忽略不计)( )m.
A.17B.16C.15D.14
15．如图,在正方形中,点E,F分别是,上的点,,相交于点M.点N是的中点,若,,则的长为( )
A.B.C.2D.
二、填空题
16．函数中自变量x的取值范围是______.
17．某校举办了以“展礼仪风采,树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、考止形态这三项的得分分别为95分,80分,80分,若依次按照40%,25%,35%的百分比确定成绩,该选手的成绩是______.
18．若直线(k为常数,)经过点,则该直线与x轴的交点坐标为______.
19．如图,在矩形中,点E是边上一点,将沿折叠,使点B落在边上的F处,已知,,则的长为______.
三、解答题
20．计算：
(1)；
(2).
21．如图,每个小正方形的边长都为1.
(1)四边形的面积________；
(2)四边形的周长________；
(3)与有什么关系？请说明理由.
22．为了解七、八年级学生对消防知识的掌握情况,某校对七年级和八年级学生进行了消防知识的测试,现从中各随机选出20名同学的成绩进行分析,将学生成绩分为A、B、C、D四个等级.分别是A：,B：,C：,D：,其中,七年级学生的成绩为：66,75,76,78,79,81,82,83,84,86,86,88,88,88,91,92,94,95,96,96.
八年级等级C的学生成绩为：87,81,86,83,88,82,89
两组数据的平均数、中位数、众数、方差如下表：
八年级学生成绩扇形统计图
根据以上信息,解答下列问题：
(1)填空：_____________________________________；
(2)根据以上数据,你认为在此次知识测试中,哪个年级的成绩更好？请说明理由；(一条理由即可)
(3)若该校七年级有760名学生参加测试,八年级有720名学生参加测试,请估计两个年级参加测试学生中成绩优秀(大于或等于90分)的学生共有多少人？
23．蓄电池发展水平是制约新能源汽车发展的关键要素.小明爸爸根据自家电动汽车仪表显示,感觉蓄电池充满电后,用前半部分电量所行驶的路程,总要比用后半部分电量行驶的路程更远一些.于是小明细心观察了充满电后汽车的行驶情况,并将蓄电池剩余电量y(千瓦时)和已行驶路程x(千米)的相关数据,用函数图象表示如下(如图).
(1)根据图象,直接写出剩余电量为35千瓦时时,汽车已行驶的路程为______千米；
(2)求该汽车剩余电量为30千瓦时时,已行驶的路程是多少？
24．如图,菱形的对角线、相交于点O,E是的中点,点F,G在上,,.
(1)求证：四边形为矩形；
(2)若,,求和的长.
25．为迎接校园艺术节的到来,学校啦啦操社团欲购买A,B两种不同类型的花球,已知2个A型花球与3个B型花球共需66元,3个A型花球与4个B型花球共需93元.
(1)求A,B两种类型花球的单价各是多少元？
(2)啦啦操社团计划购买这两种花球共50个.设A型花球购买a个,购买两种型号的总费用为w元,请求出w与a之间的函数关系式；并求当购买A型花球不少于15个,A型花球购买多少个时,总费用最少？求出最少总费用.
26．如图,直线：与过点的直线交于点,与x轴交于点B.
(1)求直线的解析式；
(2)点M在直线上,轴,交直线于点N,若,求点M的坐标.
27．【活动探究】
(1)数学活动课上,老师出示了一个问题：如图①,正方形中,点E是的中点,将正方形沿折叠,得到点B的对应点为,延长交线段于点P,连接.求的度数.
【追本溯源】
(2)小瑞受此问题启发,逆向思考并提出新的问题：如图②,正方形的边长为6,点E,F分别在,上运动,连接,,.若,试猜想,,的数量关系是_____________,并加以证明.
【拓展迁移】
(3)小波深入研究以上两个问题,发现并提出新的探究点：如图③,是的高,,若,,求的面积.
参考答案
1．答案：C
解析：A、,不是最简二次根式,不符合题意；
B、,不是最简二次根式,不符合题意；
C、是最简二次根式,符合题意；
D、,不是最简二次根式,不符合题意；
故选C.
2．答案：B
解析：A、当时,,故选项A不符合题意；
B、当时,,故选项B符合题意；
C、当时,,故选项C不符合题意；
D、当时,,故选项D不符合题意；
故选：B.
3．答案：D
解析：A、,故该选项是错误的；
B、,故该选项是错误的；
C、,故该选项是错误的；
D、,故该选项是正确的；
故选：D.
4．答案：D
解析：A、∵,
∴长为,,1的三条线段可以组成直角三角形,故此选项不符合题意；
B、∵,
∴长为3,4,5的三条线段可以组成直角三角形,故此选项不符合题意；
C、∵,
∴长为6,8,10的三条线段可以组成直角三角形,故此选项不符合题意；
D、∵,
∴长为,,的三条线段不可以组成直角三角形,故此选项符合题意；
故选：D.
5．答案：B
解析：A、是一次函数,不是正比例函数,所以本选项不符合题意；
B、是正比例函数,所以本选项符合题意；
C、不是正比例函数,不是正比例函数,所以本选项不符合题意；
D、不是正比例函数,所以本选项不符合题意.
故选：B.
6．答案：C
解析：乙和丙的平均成绩比甲和丁好,
从乙和丙中选择一人参加比赛,
又,
选择丙参赛,
故选：C.
7．答案：C
解析：,
∵与最简二次根式能合并,
,
,
故选：C.
8．答案：C
解析：如图所示,
∵,
∴,,,
∴,
又∵平分,
∴,
∴,
∴,
∴,
故选：C.
9．答案：A
解析：∵,
∴y随x的增大而减小,
又,
,
故选：A.
10．答案：D
解析：A、③有一组邻边相等的矩形是正方形,条件正确,不符合题意.
B、②对角线互相垂直的平行四边形是菱形,条件正确,不符合题意.
C、④有一个角是直角的菱形是正方形,条件正确,不符合题意.
D、①一条对角线与其中一边相等的平行四边形不一定是矩形,条件错误,符合题意.
故选：D.
11．答案：B
解析：∵四边形是平行四边形,,
∴是菱形,
∴；
∵点E,F分别为,的中点,
∴是的中位线,,
∴,
由(1)可知,四边形是菱形,
∴,
在中,由勾股定理得：,
∴菱形的周长.
故选：B.
12．答案：C
解析：把点代入得,
∴点P坐标为,
由图象得方程组的解为.
故选：C.
13．答案：D
解析：根据题意和图形的形状,可知水的最大深度h与时间t之间的关系分为两段,先快后慢.
故选：D.
14．答案：A
解析：如图,标注各点,过点D作于点E,
,,
设旗杆的高度为x,则,,
在中,,
,
解得：,
故选：A.
15．答案：B
解析：∵,,
∴正方形的边长为3,
在中,由勾股定理得,
∵,,,
∴,
∴,
∵,
∴,
∴,
∵点N是的中点,即为斜边上的中线,
∴,
故选：B.
16．答案：
解析：根据题意得：,
解得：.
故答案为：.
17．答案：86分
解析：∵(分),
∴该选手的成绩是86分.
故答案为：86分.
18．答案：
解析：把点代入,
得：,
解得：,
∴直线的解析式为：,
令,则,
解得：,
∴直线与x轴的交点坐标为.
故答案为：.
19．答案：/
解析：由翻折的性质可知,,,
在中,,,
,
,
设,则,,
在中,由勾股定理得：,
即,
解得,
即.
故答案为：.
20．答案：(1)9
(2)
解析：(1)
；
(2)
.
21．答案：(1)12
(2)
(3)相等,且垂直
解析：(1)四边形的面积；
故答案为：12；
(2)四边形的周长为
；
故答案为：；
(3)理由：如图所示,连接.
根据勾股定理,得,
∴,
∴是直角三角形,
∴,
所以,且.
22．答案：(1)88,87.5,35
(2)八年级学生的成绩更好,理由见解析
(3)估计两个年级参加测试学生中成绩优秀(大于或等于90分)的学生共有516人
解析：(1)七年级成绩的众数分,八年级A、B登记学生人数为(人),则其成绩的中位数(分)
C等级人数所占百分比为.
故答案为：,,.
(2)八年级学生的成绩更好,理由如下(写出一条理由即可)
七、八年级学生在此次知识测试中成绩的平均数均相同,都是85.2分,八年级学生在此次知识测试中成绩的中位数87.5分高于七年级在此次知识测试中成绩的中位数86分(答案不唯一).
(3)(人)
答：估计两个年级参加测试学生中成绩优秀(大于或等于90分)的学生共有516人.
23．答案：(1)150
(2)该汽车剩余电量为30千瓦时时,已行驶的路程是160千米
解析：(1)由函数图象可知,剩余电量为35千瓦时时,汽车已行驶的路程为千米,
故答案为：150；
(2)设段的函数解析式为,
将点和代入解析式得：
,
解得：,
段的函数解析式为,
当时,,
解得：,
即该汽车剩余电量为30千瓦时时,已行驶的路程是160千米.
24．答案：(1)证明见解析
(2)5,1
解析：(1)证明：∵点O为菱形对角线、的交点,
∴,
∵点E为边的中点,
∴,
∴,
∵,
∴四边形为平行四边形,
又,
∴,
∴四边形为矩形；
(2)∵,,
∴,
∴,
∵四边形为菱形,点E为中点,
∴,
在中,,
∴.
25．答案：(1)A型花球每个15元,B型花球每个12元
(2)当A型花球15个时,总费用最少,最少总费用为645元
解析：(1)设A型花球每个x元,B型花球每个y元,
根据题意,可得,
解得,
答：A型花球每个15元,B型花球每个12元；
(2)根据题意,可得,
∵购买A型花球不少于15个,
∴,
∵,
∴w随着a的增大而增大,
∴当时,w的值最小,.
答：当A型花球15个时,总费用最少,最少总费用为645元.
26．答案：(1)
(2)或
解析：(1)在中,令,得,
∴,
把代入得,
∴,
设直线的解析式为,
∴,解得,
∴直线的解析式为；
(2),
设,由轴,得,
,
解得或,
∴或.
27．答案：(1)
(2),证明见解析
(3)135
解析：(1)∵将正方形沿折叠,得到点B的对应点为F,
∴,,.
∵四边形是正方形,
∴,,
∴,,
∵,
∴,
∴,
∵,
∴；
(2)如图：延长到G,使,连接,则,
∵,
∴,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,即.
(3)将沿翻折得到,沿翻折得到,延长,交于点Q,
∴,,,,,
∴四边形是正方形,
∴,,
设,则,,
∵在中,,即,解得,
∴,
∴,
∴.
甲
乙
丙
丁
平均数
88
92
92
88
方差
0.9
1.5
1
1.8
学生
平均数
中位数
众数
方差
七年级
85.2
86
a
59.66
八年级
85.2
b
91
91.76