中职数学高教版（2021·十四五）基础模块 下册7.1 多面体精品课件ppt

这是一份中职数学高教版（2021·十四五）基础模块 下册7.1 多面体精品课件ppt，共16页。PPT课件主要包含了长方体的直观图等内容，欢迎下载使用。

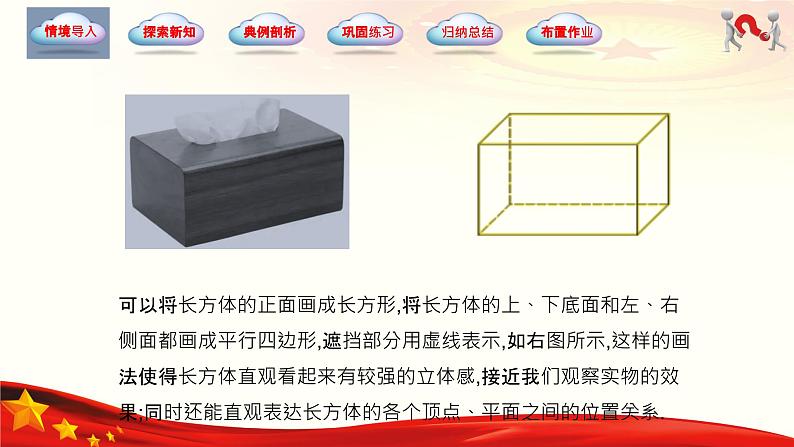
如图所示是长方体的实物图，在平面中画出这个立体图形时，我们如何体现立体感？
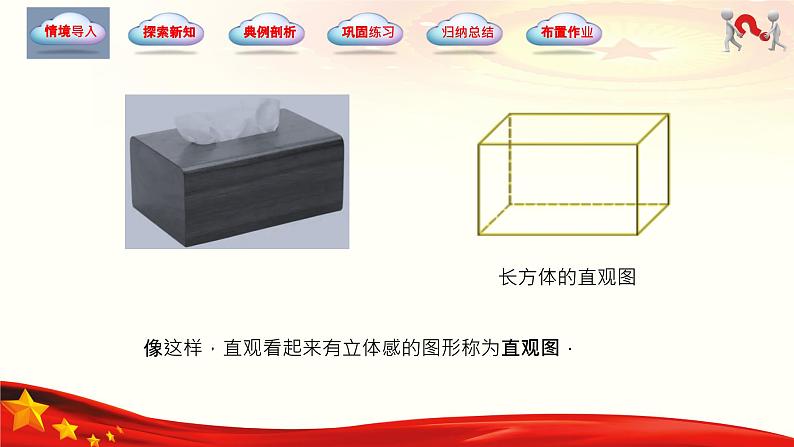
可以将长方体的正面画成长方形,将长方体的上、下底面和左、右侧面都画成平行四边形,遮挡部分用虚线表示,如右图所示,这样的画法使得长方体直观看起来有较强的立体感,接近我们观察实物的效果;同时还能直观表达长方体的各个顶点、平面之间的位置关系.
像这样，直观看起来有立体感的图形称为直观图．
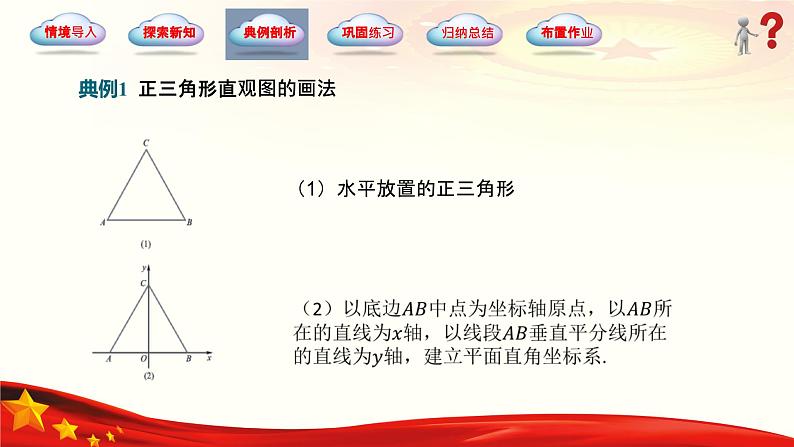
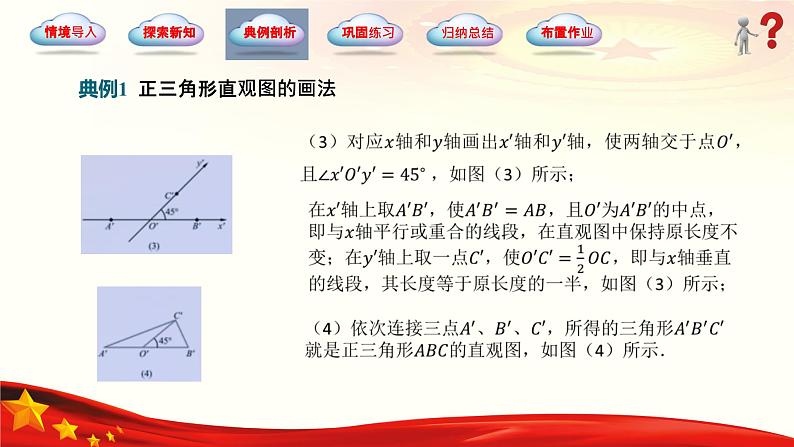
典例1 正三角形直观图的画法
（1）水平放置的正三角形
以上画直观图的方法称为斜二测画法
对斜二测画法中“斜”“二测”的解读“斜”是指在已知图形的xOy平面内与x轴垂直的线段，在直观图中均与x轴成45°或135°；“二测”是指两种度量形式，即在直观图中，平行于x′轴或z′轴的线段长度不变；平行于y′轴的线段长度变为原来的一半．斜二测画法画图的关键是在原图中找到决定图形位置与形状的点，并在直观图中画出．
用斜二测画法画水平放置的平面图形的直观图的步骤
(1)在已知图形中取互相垂直的x轴和y轴，两轴相交于点O，画直观图时，把x轴和y轴画成对应的x轴和y轴，使xOy ＝45（或135 ），x轴和y轴确定的平面表示水平面．
(2)已知图形中与x轴平行（或重合）的线段，在直观图中分别画成与x轴平行（或重合）的线段，且长度不变；已知图形中与y轴平行（或重合）的线段，在直观图中分别画成与y轴平行（或重合）的线段，且长度为原来的一半．
（3）连接有关线段，擦去作图过程中的辅助线．
典例2 用斜二测画法画长、宽、高分别是4 cm、3 cm、2 cm的长方体ABCD－A′B′C′D′的直观图．
(3)画侧棱，过A、B、C、D各点分别作z轴的平行线，并在这些平行线上分别截取2 cm长的线段AA′、BB′、CC′、DD′．
(4)成图．顺次连接A′、B′、C′、D′，并加以整理(擦掉辅助线，将被遮挡的线改为虚线)，就得到长方体的直观图(如图②)．
用斜二测画法画空间几何体的直观图的步骤
(1)画底面，这时使用平面图形的斜二测画法即可．
(2) 画z′轴，z′轴过点O′，且与x′轴的夹角为90°，并画出高线(与原图高线相等，画正棱柱时只需要画侧棱即可)，连线成图．
（3）擦去辅助线，被遮线用虚线表示．
【巩固1】画边长为1 cm的正三角形的水平放置的直观图．
[解析]　(1)如图所示，以BC边所在直线为x轴，以BC边上的高线AO所在直线为y轴，再画对应的x′轴与y′轴，两轴相交于点O′，使∠x′O′y′＝45°．
【巩固2】画一个水平放置的长为4，宽为3，高为2的长方体的直观图．
解：（1）用斜二测画法画一个水平放置的长方形的直观图ABCD（保留坐标轴），如图．
（2）过点A作z轴，使之垂直于x轴，在z轴上截取AA=2，如图．
（3）过B，C，D分别作z轴的平行线BB，CC，DD，并使BB=CC=DD=2，然后连接AB，BC，CD，DA ．
（4）擦去作图过程中的辅助线，并把被面遮挡的线段改成虚线（或擦除）．由此得到的就是长方体的直观图，如图．