苏科版八年级上册1.3 探索三角形全等的条件课时作业

这是一份苏科版八年级上册1.3 探索三角形全等的条件课时作业，共15页。试卷主要包含了3　探索三角形全等的条件等内容，欢迎下载使用。
基础过关全练
知识点1 基本事实“边角边(SAS)”
1.【新考法】【教材变式·P35T2】如图,小明和小丽用下面的方法测量位于池塘两端的A、B两点间的距离:先在池塘旁边取一点O,使点O能直接到达A、B两点,连接AO并延长到C,使OC=OA,连接BO并延长到D,使OD=OB,这时,只要测出线段 的长度就可知A、B两点间的距离,这是根据 判定 ≌ .
2.(2022湖北黄石中考)如图,在△ABC和△ADE中,AB=AC,
AD=AE,∠BAC=∠DAE=90°,且点D在线段BC上,连接CE.求证:△ABD≌△ACE.

知识点2 基本事实“角边角(ASA)”
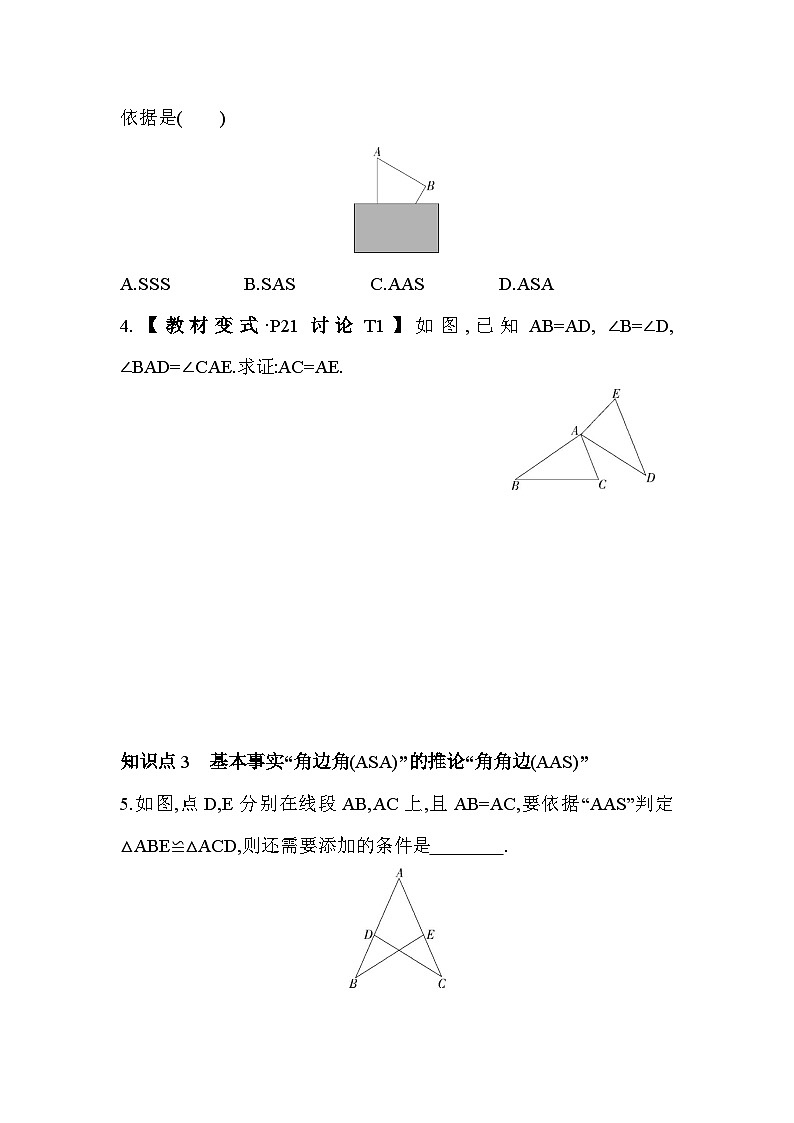
3.【教材变式·P17讨论T1】如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就重新画出了一个与原来完全一样的三角形,他的依据是( )
A.SSS B.SAS C.AAS D.ASA
4.【教材变式·P21讨论T1】如图,已知AB=AD, ∠B=∠D, ∠BAD=∠CAE.求证:AC=AE.

知识点3 基本事实“角边角(ASA)”的推论“角角边(AAS)”
5.如图,点D,E分别在线段AB,AC上,且AB=AC,要依据“AAS”判定△ABE≌△ACD,则还需要添加的条件是 .
6.(2022广东中考)如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.

知识点4 基本事实“边边边(SSS)”
7.如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,求证:CB=CD.

知识点5 三角形的稳定性
8.在实际生活中,我们经常利用一些几何图形的稳定性或不稳定性,下列实物图中没有利用三角形稳定性的是( )

A.钢架桥 B.屋顶钢架

C.起重机 D.活动挂架
知识点6 用尺规作角平分线和垂线
9.【新考法】(2022浙江舟山中考)用尺规作一个角的平分线,下列作法中错误的是( )

A B C D
10.【尺规作图】(2022山东威海中考)过直线l外一点P作直线l的垂线PQ.四个选项中尺规作图错误的是( )

A B C D
知识点7 斜边、直角边(HL)定理
11.【教材变式·P28例8】如图,AC⊥BC,AD⊥BD,AD=BC,
CE⊥AB,DF⊥AB,垂足分别是E,F,求证:CE=DF.

能力提升全练
12.(2022湖南永州中考,2,★☆☆)下列多边形具有稳定性的是( )

A B C D
13.(2022江苏南通中考,14,★☆☆)如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,要使△ABC≌△DEF,只需添加一个条件,则这个条件可以是 .
14.(2022广东广州中考,18,★☆☆)如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE,求证:△ABD≌△ACE.
15.(2022湖南益阳中考,20,★☆☆)如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.
求证:△CED≌△ABC.

16.(2022江苏淮安中考,19,★☆☆)已知:如图,点A、D、C、F在一条直线上,且AD=CF,AB=DE,∠BAC=∠EDF.求证:∠B=∠E.

17.【三垂直模型】(2023江苏南通期中,25,★★★)如图1,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,过A作AD⊥l,垂足为D,过B作BE⊥l,垂足为E.
(1)求证:△ADC≌△CEB;
(2)若AD=5,DE=13,求BE的长;
(3)如图2,延长AD至F,连接CF,过点C作CG⊥CF,且CG=CF,连接BG交直线l于点H,若S△CGH=30,CD=10,则AF= .

图1 图2
素养探究全练
18.【推理能力】(2021江苏太仓期末)【问题提出】
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角分别相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后对∠B进行分类,可分为∠B是“直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据 可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)

图① 图② 图③
答案全解全析
基础过关全练
1.答案 CD;SAS;△AOB;△COD
解析 在△AOB和△COD中,AO=CO,∠AOB=∠COD,BO=DO,
∴△AOB≌△COD(SAS).
∴AB=CD,即线段CD的长度就是A、B两点间的距离.
2.证明 ∵∠BAC=∠DAE=90°,
∴∠BAC-∠CAD=∠DAE-∠CAD,即∠BAD=∠CAE.
在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).
3.D 只要量出AB的长和∠A、∠B的度数,再画出一个三角形DEF,使EF=AB,∠E=∠A,∠F=∠B即可.故选D.
4.证明 ∵∠BAD=∠CAE,
∴∠BAD-∠CAD=∠CAE-∠CAD,
即∠BAC=∠DAE.
在△BAC与△DAE中,∠B=∠D,AB=AD,∠BAC=∠DAE,
∴△BAC≌△DAE(ASA),
∴AC= AE.
5.答案 ∠ADC=∠AEB(答案不唯一)
解析 添加的条件是∠ADC=∠AEB,根据AAS即可推出△ABE≌△ACD.(答案不唯一)
6.证明 ∵PD⊥OA,PE⊥OB,
∴∠ODP=∠OEP=90°.
∵∠AOC=∠BOC,
∴∠DOP=∠EOP.
在△OPD和△OPE中,∠ODP=∠OEP,∠DOP=∠EOP,OP=OP,
∴△OPD≌△OPE(AAS).
7.证明 如图,连接AC,
在△ACE和△ACF中,AE=AF,CE=CF,AC=AC,
∴△ACE≌△ACF(SSS),
∴∠EAC=∠FAC.
在△ACB和△ACD中,∠BAC=∠DAC,∠B=∠D=90°,AC=AC,
∴△ACB≌△ACD(AAS),
∴CB=CD.
8.D 选项A、B、C都利用了三角形的稳定性,不符合题意,故选D.
9.D 本题考查作已知角的平分线的方法.
10.C 选项A,如图,连接PA,PB,QA,QB,
∵PA=PB,
∴点P在线段AB的垂直平分线上.
∵QA=QB,
∴点Q在线段AB的垂直平分线上,
∴PQ⊥l,故此选项不符合题意.
选项B,如图,连接PA,PB,QA,QB.
∵PA=QA,
∴点A在线段PQ的垂直平分线上.
∵PB=QB,
∴点B在线段PQ的垂直平分线上,
∴PQ⊥l,故此选项不符合题意.
选项C,无法证明PQ⊥l,故此选项符合题意.
选项D,如图,连接PA,PB,QA,QB.
∵PA=QA,
∴点A在线段PQ的垂直平分线上.
∵PB=QB,
∴点B在线段PQ的垂直平分线上,
∴PQ⊥l,故此选项不符合题意.故选C.
11.证明 ∵AC⊥BC,AD⊥BD,
∴∠ACB=∠BDA=90°.
在Rt△ABC和Rt△BAD中,AB=BA,BC=AD,
∴Rt△ABC≌Rt△BAD(HL),
∴S△ABC=S△BAD.
∵CE⊥AB于点E,DF⊥AB于点F,
∴12AB·CE=12AB·DF,
∴CE=DF.
能力提升全练
12.D 三角形具有稳定性,其他多边形不具有稳定性.故选D.
13.答案 AB=DE(答案不唯一)
解析 ∵AB∥ED,∴∠B=∠E.
∵AC∥DF,∴∠ACB=∠DFE.
∵AB=DE,
∴△ABC≌△DEF(AAS).故答案为AB=DE.(答案不唯一)
14.证明 ∵∠B=∠C,∴AB=AC.
在△ABD和△ACE中,AB=AC,∠B=∠C,BD=CE,
∴△ABD≌△ACE(SAS).
15.证明 ∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°.
∵CD∥AB,
∴∠A=∠DCE.
在△CED和△ABC中,∠DCE=∠A,CE=AB,∠DEC=∠B,
∴△CED≌△ABC(ASA).
16.证明 ∵AD=CF,∴AD+CD=CF+CD,
即AC=DF.
在△ABC和△DEF中,AB=DE,∠BAC=∠EDF,AC=DF,
∴△ABC≌△DEF(SAS),
∴∠B=∠E.
17.解析 (1)证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=∠ACB=90°.
∴∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB.
在△ADC和△CEB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,
∴△ADC≌△CEB(AAS).
(2)∵△ADC≌△CEB,AD=5,
∴AD=CE=5,CD=BE.
∵DE=13,∴BE=CD=DE-CE=13-5=8.
(3)如图,过点G作GM⊥l于M.
∵CG⊥CF,AD⊥l,∴∠CFD+∠DCF=∠DCF+∠MCG=90°,
∴∠CFD=∠MCG.
∵∠CDF=∠CMG=90°,CF=CG,
∴△CDF≌△GMC(AAS),
∴CD=GM=10,DF=MC.
∵S△CGH=30,∴12CH·GM=30,∴CH=2×30GM=6010=6.
∵△ADC≌△CEB,
∴CD=BE=10,AD=CE,∴BE=GM.
∵∠BEH=∠GMH=90°,∠BHE=∠GHM,
∴△BEH≌△GMH(AAS),∴EH=MH,
∴AF=AD+DF=CE+CM=CH-EH+CH+EH
=2CH=2×6=12.
故答案为12.
素养探究全练
18.解析 (1)HL.
(2)证明:如图,过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H,
∵∠ABC=∠DEF,且∠ABC、∠DEF都是钝角,
∴180°-∠ABC=180°-∠DEF,即∠CBG=∠FEH.
在△CBG和△FEH中,∠CBG=∠FEH,∠G=∠H=90°,BC=EF,
∴△CBG≌△FEH(AAS),∴CG=FH.
在Rt△ACG和Rt△DFH中,AC=DF,CG=FH,
∴Rt△ACG≌Rt△DFH(HL),∴∠A=∠D.
在△ABC和△DEF中,∠A=∠D,∠ABC=∠DEF,AC=DF,
∴△ABC≌△DEF(AAS).
(3)如图,△DEF和△ABC不全等.