云南省楚雄彝族自治州2023-2024学年八年级下学期期末数学试卷(含答案)

这是一份云南省楚雄彝族自治州2023-2024学年八年级下学期期末数学试卷(含答案)，共14页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列各数中,属于正整数的是( )
A.0B.C.1D.
2．下列二次根式中,属于最简二次根式的是( )
A.B.C.D.
3．近十年来,我国扎实开展国土绿化行动,持续推进科学绿化,累计完成国土绿化面积1680000000亩,将数据“1680000000”用科学记数法表示为( )
A.B.
C.D.
4．以下列各组数为边长,能构成直角三角形的是( )
A.1,,B.1,1,2C.2,3,4D.,,
5．如图,在中,D,E分别为,的中点.若,则的长为( )
A.3B.6C.9D.12
6．甲、乙、丙、丁四人各进行10次射击测试,他们的平均成绩相同,方差分别是,,,,则射击成绩最稳定的是( )
A.甲B.乙C.丙D.丁
7．菱形具有而矩形不具有的性质是( )
A.四边相等B.对角线相等C.对角相等D.邻角互补
8．按一定规律排列的单项式：,,,,.则第7个单项式是( )
A.B.C.D.
9．已知点,都在直线上,则,的大小关系是( )
A.B.C.D.
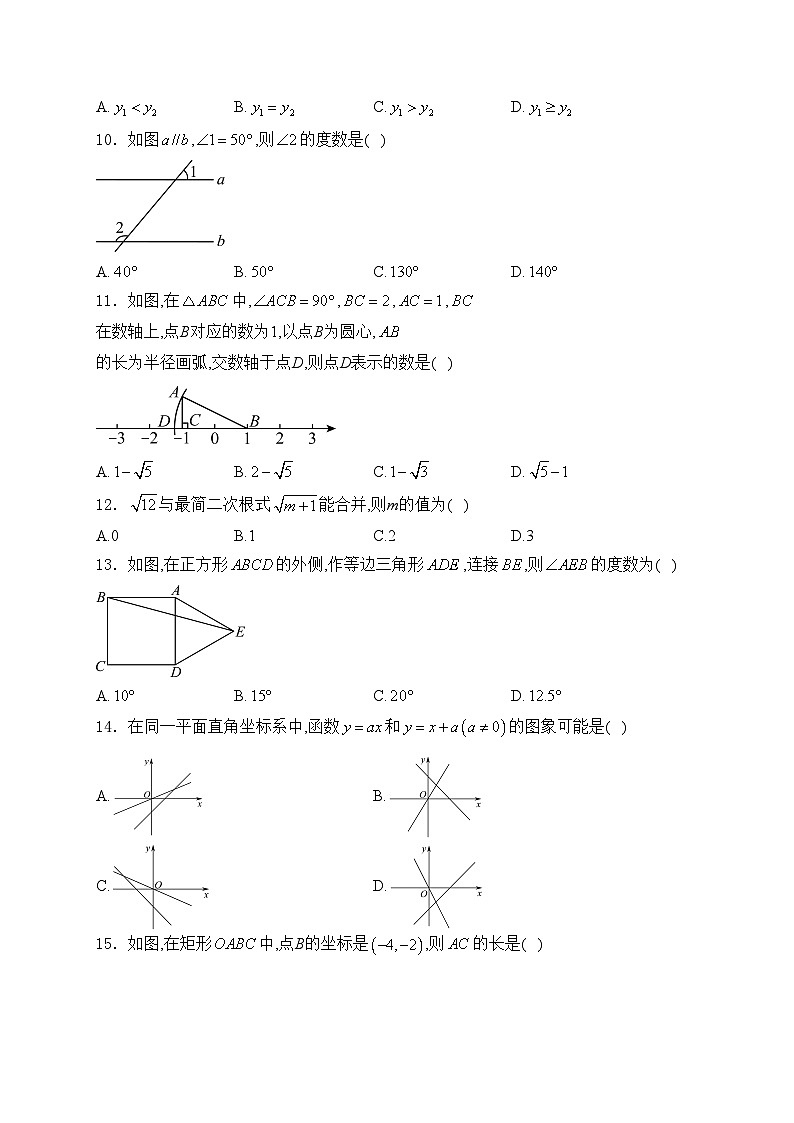
10．如图,,则的度数是( )
A.B.C.D.
11．如图,在中,,,,在数轴上,点B对应的数为1,以点B为圆心,的长为半径画弧,交数轴于点D,则点D表示的数是( )
A.B.C.D.
12．与最简二次根式能合并,则m的值为( )
A.0B.1C.2D.3
13．如图,在正方形的外侧,作等边三角形,连接,则的度数为( )
A.B.C.D.
14．在同一平面直角坐标系中,函数和的图象可能是( )
A.B.
C.D.
15．如图,在矩形中,点B的坐标是,则的长是( )
A.2B.C.4D.
二、填空题
16．若二次根式有意义,则x的取值范围是______.
17．在平行四边形中,,则的度数为______.
18．将直线向下平移7个单位长度,所得直线的解析式为______.
19．如图在的方格中,小正方形的边长均为1,点A,B,C都在格点(网格线的交点)上,则边上的高为______.
三、解答题
20．计算：.
21．如图,,,,且A,E,C,F四点共线.求证：.
22．小明从家出发骑自行车去上学,当他以往常的速度骑了一段路后,突然想起要买圆规,于是又折回到刚经过的文具店,买到圆规后继续骑车去学校.如图,这是他本次上学过程中离家距离(单位：米)与所用时间(单位：分钟)的关系图,根据图象解答下列问题.
(1)小明在文具店停留了________分钟,文具店到学校的路程是________米.
(2)若小明不买文具,以往常的速度去学校,则他能提前多长时间到达学校？
23．某校为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球.若购买3个篮球和1个足球共需420元,购买2个篮球和3个足球共需560元,求每个篮球和每个足球的售价.
24．如图,大风把一棵树刮断,已知被刮断前树高,倒下后树干顶部离根部距离,求树折断处与地面的距离(即的长).
25．如图,在菱形中,分别延长,至点E,F,使,,连接,,,.
(1)求证：四边形是矩形.
(2)若,,求矩形的面积.
26．为了解某班学生对食品安全知识的掌握情况,老师从班级学生中任意选取20人,随机分成甲、乙两个小组(每组10人)进行食品安全知识竞赛,根据竞赛成绩绘制出下面的统计图和统计表.乙组学生答对题数：1,2,3,3,3,4,4,4,4,5.根据信息,解答下列问题.
甲组学生答对题数条形统计图
甲、乙组学生答对题数统计表
(1)填空：______,______,______.
(2)请你运用所学的统计知识,判断哪个小组的学生食品安全意识更强.
27．如图,直线：与直线交于点,与y轴交于点B,直线与x轴交于点,连接.
(1)求直线的解析式.
(2)求的面积.
(3)在x轴上是否存在一点P,使得是以为直角边的直角三角形？若存在,求出点P的坐标；若不存在,请说明理由.
参考答案
1．答案：C
解析：0既不是正数,也不是负数；是无理数；1是正整数；是正分数,
故选：C.
2．答案：D
解析：∵,,,
∴是最简二次根式,
故选：D.
3．答案：B
解析：,
故选：B.
4．答案：A
解析：A.,1,,能构成直角三角形,符合题意；
B.,1,1,2不能构成直角三角形,不合题意；
C.,2,3,4不能构成直角三角形,不合题意；
D.,,,不能构成直角三角形,不合题意；
故选A.
5．答案：D
解析：D,E分别为,的中点,
是的中位线,
又,
.
故选D.
6．答案：B
解析：平均成绩相同,方差分别是,,,,
,
乙的射击成绩最稳定,
故选：B.
7．答案：A
解析：A、四边相等,菱形具有而矩形不具有,故本选项符合题意；
B、对角线相等,矩形具有而菱形不具有,故本选项不符合题意；
C、对角相等,菱形具有,矩形具有,故本选项不符合题意；
D、邻角互补,菱形具有而矩形也具有,故本选项不符合题意；
故选：A.
8．答案：B
解析：由题意得,第n个单项式为,
∴第7个单项式是,
故选：B.
9．答案：C
解析：∵,,
∴y随x的增大而减小,
∵,
∴,
故选：C.
10．答案：C
解析：∵,,
∴,
∴,
故选：C.
11．答案：A
解析：在中,,,,
点B对应的数为1,
点D表示的数是,
故选：A.
12．答案：C
解析：,
∵即与最简二次根式能合并,
∴,
解得,
故选：C.
13．答案：B
解析：四边形是正方形,
,,
是等边三角形,
,,
,,
,
,
,
,
故选：B.
14．答案：D
解析：A.由函数得,与图像的矛盾,故本选项不符合题意；
B.函数所过象限错误,故本选项不符合题意；
C.函数所过象限错误,故本选项不符合题意；
D.由函数得,与图像的一致,故本选项符合题意.
故选：D.
15．答案：D
解析：连接,
∵点B的坐标是,
∴,
∵四边形是矩形,
∴,
故选：D.
16．答案：
解析：根据题意,使二次根式有意义,即,
解得：.
故答案为：.
17．答案：
解析：∵四边形是平行四边形,
∴,
∵,
∴,
故答案为：.
18．答案：/
解析：将直线向下平移7个单位长度,所得直线的解析式为,即.
故答案为：.
19．答案：
解析：由题意可得,
又,
边上的高为,
故答案为：.
20．答案：1
解析：
.
21．答案：证明见解析
解析：证明：,
,即.
在和中,
,
.
22．答案：(1)3；1200
(2)小明不买文具,以往常的速度去学校,能提前6分钟到达学校
解析：(1)(分钟).
小明在文具店停留了3分钟,
由题意可知,小明家到学校的距离是1800米,
(米).
即文具店到学校的距离是1200米.
故答案为：3,1200；
(2)小明往常的速度为(米分),
去学校需要花费的时间为(分钟).
提前到达学校的时间为(分钟).
答：小明不买文具,以往常的速度去学校,能提前6分钟到达学校.
23．答案：每个篮球的售价是100元,每个足球的售价是120元
解析：设每个篮球的售价是x元,每个足球的售价是y元.根据题意得：
解得：,
答：每个篮球的售价是100元,每个足球的售价是120元.
24．答案：
解析：由题意知,,,即,
由勾股定理得,,即,
解得,,
∴树折断处与地面的距离(即的长)为.
25．答案：(1)证明见解析
(2)
解析：(1)证明：∵,,
∴四边形是平行四边形,
∵四边形是菱形,
∴,
∴,
∴,
∴四边形是矩形；
(2)∵四边形是菱形,,,
∴,,
∴和是等边三角形,
∴,,
∵四边形是矩形,
∴,
∴,
∴,
∴,
∴矩形的面积为：.
26．答案：(1)3.7；3.5；4
(2)甲组学生的食品安全意识更强
解析：(1)由图可得,
甲组的平均数为,
把乙组的数据按照从小到大的顺序排列,除以中间的两个数为3、4,
∴中位数,
乙组数据中,4出现了4次,出现次数最多,
∴众数,
故答案为：3.7；3.5；4.
(2)∵甲组的平均数和中位数高于乙组的平均数和中位数,且甲、乙两组的众数相等,
∴甲组学生的食品安全意识更强.
27．答案：(1)
(2)
(3)存在,点P的坐标为或
解析：(1)点在直线上,
,
点.
设直线的解析式为.
将点,代入,得,
解得,
直线的解析式为.
(2)如图1,记直线与x轴的交点为D.
将代入,解得,
点.
将代入,解得,
点,
,
.
(3)存在.
设点.
分以下两种情况：
①如图2,当时,
在中,存在,
即,
解得.
点；
②如图3,当时,
在中,存在,
即,
解得,
点.
综上所述,点P的坐标为或.
平均数
中位数
众数
甲组
a
4
4
乙组
3.3
b
c