高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文内容课件ppt

这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文内容课件ppt，共40页。PPT课件主要包含了自主预习·新知导学，合作探究·释疑解惑，思想方法，随堂练习，答案C等内容，欢迎下载使用。
自主预习·新知导学
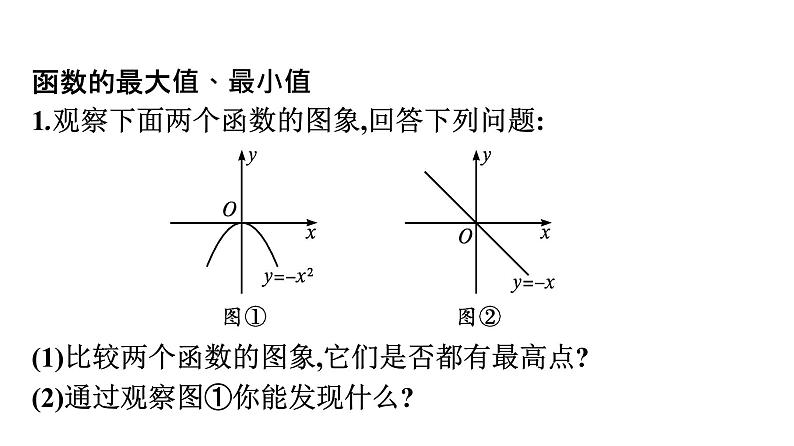
函数的最大值、最小值1.观察下面两个函数的图象,回答下列问题:
(1)比较两个函数的图象,它们是否都有最高点?(2)通过观察图①你能发现什么?
提示:(1)题图①中函数y=-x2的图象上有一个最高点;题图②中函数y=-x的图象上没有最高点.(2)对任意x∈R,都有f(x)≤f(0).
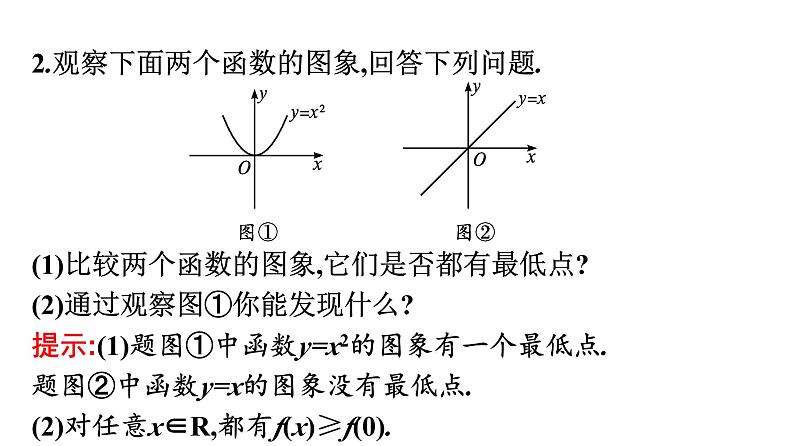
提示:(1)题图①中函数y=x2的图象有一个最低点.题图②中函数y=x的图象没有最低点.(2)对任意x∈R,都有f(x)≥f(0).
4.已知函数f(x)在区间[-2,2]上的图象如图所示,则该函数的最小值、最大值分别是(　　) 　　　　　　　　　　　　　　　　A.f(-2),0B.0,2C.f(-2),2D.f(2),2解析:由题图可知,该函数的最小值为f(-2),最大值为f(1)=2.答案:C
【思考辨析】 判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.(1)任何函数都有最大(小)值.( × )(2)函数f(x)在区间[a,b]上的最值一定是f(a)或f(b).( × )(3)若对任意x∈D,都有f(x)≤M,则M是函数f(x)的最大值.( × )(4)如果一个函数f(x)在区间[a,b]上单调递减,那么函数在区间[a,b]上的最大值是f(a).( √ )
合作探究·释疑解惑
探究一 利用函数的图象求函数的最值
【例1】 作出函数y=|x-2|(x+1)的图象,说明函数的单调性,并判断其是否存在最大值和最小值.分析:去绝对值→分段函数→作图→识图→结论
反思感悟图象法求最值的步骤
(1)如图所示,在给定的平面直角坐标系内作出f(x)的图象; (2)由图象指出当x取什么值时f(x)有最值.
解:(1)由题意知,当x∈[-1,2]时,f(x)=-x2+3,其图象为二次函数图象的一部分;当x∈(2,5]时,f(x)=x-3,其图象为一次函数图象的一部分.故函数f(x)的图象如图所示: (2)由图象可知,当x=0时,f(x)有最大值3;当x=2时,f(x)有最小值-1.
探究二 利用函数的单调性求函数的最值
分析:(1)证明单调性的流程:取值→作差→变形→判断符号→结论;(2)借助函数的最值与单调性的关系,写出函数的最值.
本例已知条件不变,判断f(x)在区间[1,3]上的单调性,并求f(x)在区间[1,3]上的最值.
反思感悟1.利用函数的单调性求函数最值的一般步骤:(1)判断函数的单调性;(2)利用函数的单调性写出函数的最值.
2.函数的最值与单调性的关系:(1)若函数f(x)在区间[a,b]上单调递增(减),则f(x)在区间[a,b]上的最小(大)值是f(a),最大(小)值是f(b).(2)若函数f(x)在区间[a,b]上单调递增(减),在区间(b,c]上单调递减(增),则f(x)在区间[a,c]上的最大(小)值是f(b),最小(大)值是f(a)与f(c)中较小(大)的一个.(3)若函数f(x)在区间[a,b]上的图象是一条连续不断的曲线,则函数f(x)在区间[a,b]上一定有最值.(4)求最值时一定要注意所给区间的开闭,若是开区间,则不一定有最大(小)值.
探究三 与函数的最值有关的应用问题
(1)设该商品的日销售额为y元,请写出y关于t的函数解析式.(2)求该商品的日销售额的最大值,并指出哪一天的销售额最大.分析:读题→提取信息→建模→解模→解决实际问题
反思感悟解函数应用题的一般步骤是(1)审题.弄清题意,分清条件和结论,理顺数量关系.(2)建模.将文字语言转化成数学语言,用数学知识建立相应的数学模型.(3)解模.求解数学模型,得到数学结论.(4)还原.将用数学方法得到的结论还原为实际问题的答案.(5)反思回顾.对于数学模型得到的解,必须验证这个解对实际问题的合理性.
【变式训练2】 某租赁公司拥有汽车100辆,当每辆车的月租金为3 000元时,可全部租出,每辆车的月租金每增加50元,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金为3 600元时,能租出多少辆?(2)当每辆车的月租金为多少元时,租赁公司的月收益最大?最大月收益是多少?
利用数形结合思想与分类讨论思想求二次函数的最值【典例】 求函数y=x2-2ax-1在区间[0,2]上的最值.审题视角:对称轴方程x=a→与定区间[0,2]的相对位置关系→结合函数的单调性与图象求解
解:y=(x-a)2-1-a2.当a0)在区间[1,3]上的最大值为4,则a=　　　　　. 解析:因为a>0,所以函数y=ax+1在区间[1,3]上单调递增,因此3a+1=4,解得a=1.答案:1