新高考数学一轮复习讲义第4章　§4.2　同角三角函数基本关系式及诱导公式（2份打包，原卷版+含解析）

这是一份新高考数学一轮复习讲义第4章　§4.2　同角三角函数基本关系式及诱导公式（2份打包，原卷版+含解析），文件包含新高考数学一轮复习讲义第4章§42同角三角函数基本关系式及诱导公式原卷版doc、新高考数学一轮复习讲义第4章§42同角三角函数基本关系式及诱导公式含解析doc等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

2.掌握诱导公式，并会简单应用．
知识梳理
1．同角三角函数的基本关系
(1)平方关系：sin2α＋cs2α＝1.
(2)商数关系：eq \f(sin α,cs α)＝tan αeq \b\lc\(\rc\)(\a\vs4\al\c1(α≠\f(π,2)＋kπ，k∈Z)).
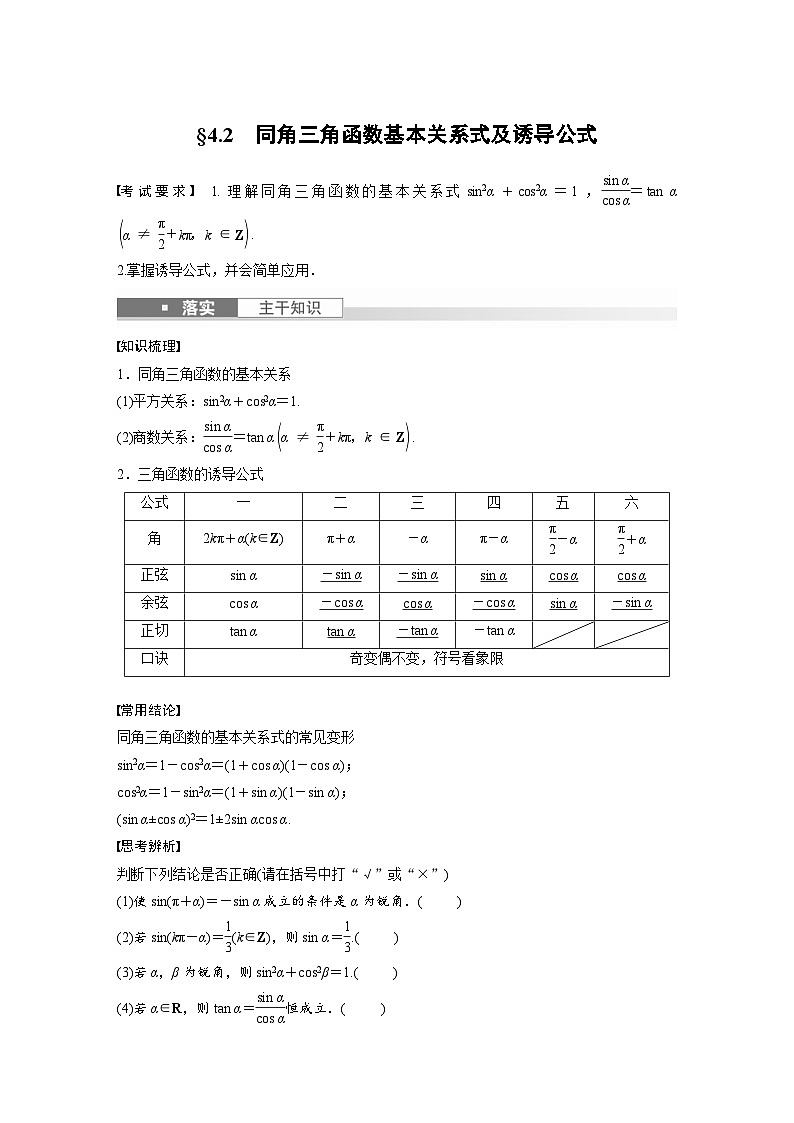
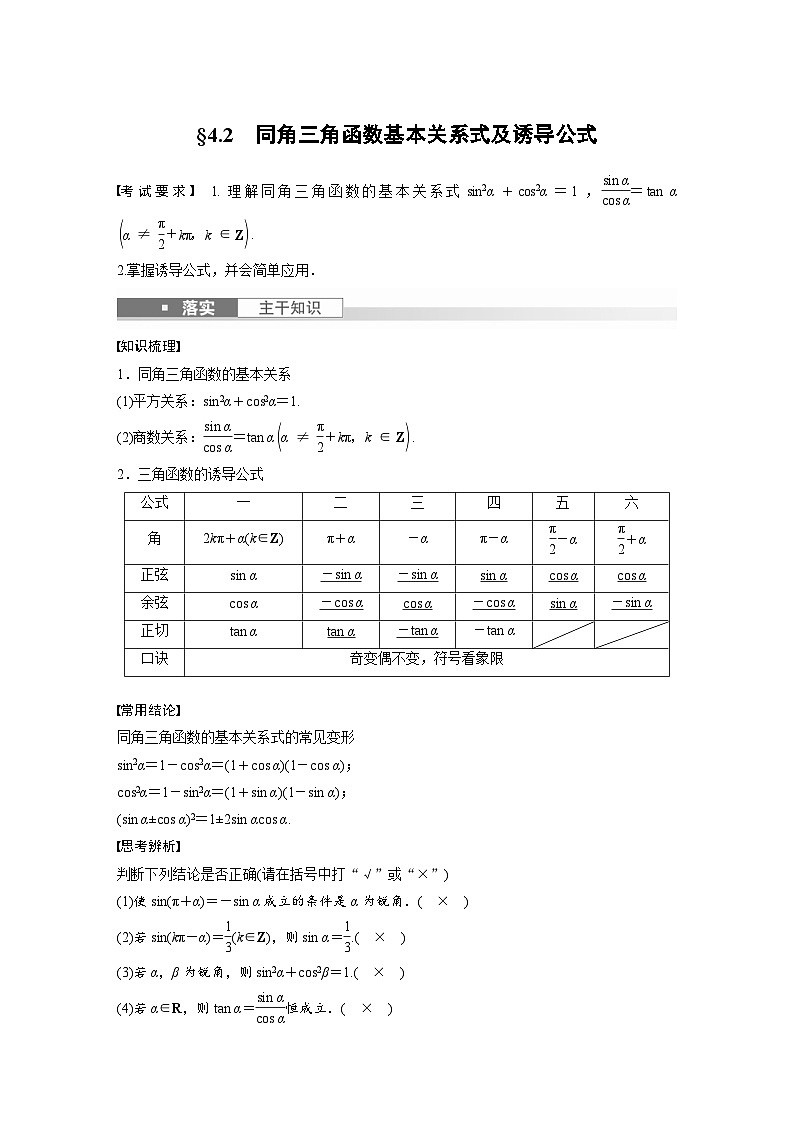
2．三角函数的诱导公式
常用结论
同角三角函数的基本关系式的常见变形
sin2α＝1－cs2α＝(1＋cs α)(1－cs α)；
cs2α＝1－sin2α＝(1＋sin α)(1－sin α)；
(sin α±cs α)2＝1±2sin αcs α.
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)使sin(π＋α)＝－sin α成立的条件是α为锐角．( )
(2)若sin(kπ－α)＝eq \f(1,3)(k∈Z)，则sin α＝eq \f(1,3).( )
(3)若α，β为锐角，则sin2α＋cs2β＝1.( )
(4)若α∈R，则tan α＝eq \f(sin α,cs α)恒成立．( )
教材改编题
1．若cs α＝eq \f(1,3)，α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，0))，则tan α等于( )
A．－eq \f(\r(2),4) B.eq \f(\r(2),4) C．－2eq \r(2) D．2eq \r(2)
2．若sin α＋cs α＝eq \f(\r(2),2)，则sin αcs α等于( )
A．－eq \f(1,2) B．－eq \f(1,4) C.eq \f(\r(2),2) D．2
3．化简eq \f(cs\b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,2))),sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)＋α)))·cs(2π－α)的结果为 ．
题型一 同角三角函数基本关系
例1 (1)(多选)已知θ∈(0，π)，sin θ＋cs θ＝eq \f(1,5)，则下列结论正确的是( )
A．θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π)) B．cs θ＝－eq \f(4,5)
C．tan θ＝－eq \f(3,4) D．sin θ－cs θ＝eq \f(7,5)
(2)已知cs α＝－eq \f(5,13)，则13sin α＋5tan α＝ .
(3)已知tan α＝2，则eq \f(3sin α－2cs α,sin α＋cs α)＝ ；eq \f(2,3)sin2α＋eq \f(1,4)cs2α＝ .
思维升华
(1)应用公式时注意方程思想的应用：对于sin α＋cs α，sin αcs α，sin α－cs α这三个式子，利用(sin α±cs α)2＝1±2sin αcs α，可以知一求二．
(2)注意公式逆用及变形应用：1＝sin2α＋cs2α，sin2α＝1－cs2α，cs2α＝1－sin2α.
跟踪训练1 (1)已知eq \f(sin α＋3cs α,3cs α－sin α)＝5，则cs2α＋eq \f(1,2)sin 2α等于( )
A.eq \f(3,5) B．－eq \f(3,5) C．－3 D．3
(2)若α∈(0，π)，sin(π－α)＋cs α＝eq \f(\r(2),3)，则sin α－cs α的值为( )
A.eq \f(\r(2),3) B．－eq \f(\r(2),3) C.eq \f(4,3) D．－eq \f(4,3)
题型二 诱导公式
例2 (1)已知x∈R，则下列等式恒成立的是( )
A．sin(3π－x)＝－sin x
B．sin eq \f(π－x,2)＝－cs eq \f(x,2)
C．cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)＋3x))＝sin 3x
D．cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)－2x))＝－sin 2x
(2)已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－x))＝eq \f(1,3)，且0思维升华 诱导公式的两个应用
(1)求值：负化正，大化小，化到锐角为终了；
(2)化简：统一角，统一名，同角名少为终了．
跟踪训练2 (1)若eq \f(sin3π－α－sin\b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,2)－α)),cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α))＋cs－π＋α)＝eq \f(1,3)，则tan α等于( )
A.eq \f(3,4) B．－eq \f(1,2) C．－eq \f(4,3) D.eq \f(1,2)
(2)已知cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋α))＝eq \f(4,5)，则sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－α))的值为( )
A.eq \f(3,5) B．－eq \f(3,5) C.eq \f(4,5) D．－eq \f(4,5)
题型三 同角三角函数基本关系式和诱导公式的综合应用
例3 (1)已知α为锐角，且2tan(π－α)－3cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋β))＋5＝0，tan(π＋α)＋6sin(π＋β)－1＝0，则sin α的值是( )
A.eq \f(3\r(2),5) B.eq \f(3\r(5),7) C.eq \f(3\r(10),10) D.eq \f(1,3)
(2)已知－π思维升华
(1)利用同角三角函数基本关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形．
(2)注意角的范围对三角函数值符号的影响．
跟踪训练3 (1)已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)－α))＋cs(π－α)＝sin α，则2sin2α－sin αcs α等于( )
A.eq \f(21,10) B.eq \f(3,2) C.eq \f(\r(3),2) D．2
(2)已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(2π,3)))＝eq \f(2,3)，其中α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))，则cseq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,6)))＝ ，sineq \b\lc\(\rc\)(\a\vs4\al\c1(2α－\f(π,3)))＝ .
课时精练
1．sin 1 620°等于( )
A．0 B.eq \f(1,2)
C．1 D．－1
2．已知α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，0))，cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α))＝eq \f(\r(3),2)，则tan α等于( )
A．－eq \r(3) B.eq \r(3) C．－eq \f(\r(3),3) D.eq \f(\r(3),3)
3．已知角α的顶点在原点，始边与x轴非负半轴重合，终边与直线2x＋y＋3＝0平行，则eq \f(sin α－cs α,sin α＋cs α)的值为( )
A．－2 B．－eq \f(1,4) C．2 D．3
4．若sin(π＋α)－cs(π－α)＝eq \f(3,5)，则sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α))cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))等于( )
A.eq \f(8,25) B．－eq \f(8,25) C.eq \f(16,25) D．－eq \f(16,25)
5．(多选)在△ABC中，下列结论正确的是( )
A．sin(A＋B)＝sin C
B．sin eq \f(B＋C,2)＝cs eq \f(A,2)
C．tan(A＋B)＝－tan Ceq \b\lc\(\rc\)(\a\vs4\al\c1(C≠\f(π,2)))
D．cs(A＋B)＝cs C
6．已知角α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，0))，且tan2α－3tan αsin α－4sin2α＝0，则sin(α＋2 023π)等于( )
A.eq \f(\r(15),4) B.eq \f(1,4) C．－eq \f(3,4) D．－eq \f(\r(15),4)
7．已知sin θ＝eq \f(1,3)，则eq \f(tan2π－θ,cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－θ))sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)＋θ)))＝ .
8．已知cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－α))＝eq \f(\r(3),3)，则cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,6)＋α))－sineq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(4π,3)))的值为 ．
9．(1)若α是第二象限角，且cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α))＝－eq \f(1,3)，求tan α的值；
(2)已知f(α)＝eq \f(sin3π－αcs2π－αsin\b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)－α)),csπ－αsin－π－α)，化简f(α)，在(1)的条件下，求f(α)的值．
10．已知角θ 的终边与单位圆x2＋y2＝1在第四象限交于点P，且点P的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，y)).
(1)求tan θ的值；
(2)求eq \f(cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－θ))＋csθ－2π,sin θ＋csπ＋θ)的值．
11．(多选)已知角α满足sin α·cs α≠0，则表达式eq \f(sinα＋kπ,sin α)＋eq \f(csα＋kπ,cs α)(k∈Z)的取值为( )
A．－2 B．－1 C．2 D．1
12．黑洞原指非常奇怪的天体，它体积小，密度大，吸引力强，任何物体到了它那里都别想再出来，数字中也有类似的“黑洞”，任意取一个数字串，长度不限，依次写出该数字串中偶数的个数、奇数的个数以及总的数字个数，把这三个数从左到右写成一个新数字串；重复以上工作，最后会得到一个反复出现的数字，我们称它为“数字黑洞”，如果把这个数字设为a，则sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(aπ,2)＋\f(π,6)))等于( )
A.eq \f(1,2) B．－eq \f(1,2) C.eq \f(\r(3),2) D．－eq \f(\r(3),2)
13．sin eq \f(4π,3)·cs eq \f(5π,6)·taneq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4π,3)))的值是 ．
14．已知sin(3π＋θ)＝eq \f(1,3)，则eq \f(csπ＋θ,cs θ[csπ－θ－1])＋eq \f(csθ－2π,sin\b\lc\(\rc\)(\a\vs4\al\c1(θ－\f(3π,2)))csθ－π－sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)＋θ)))＝ .
15．(多选)已知角θ和φ都是任意角，若满足θ＋φ＝eq \f(π,2)＋2kπ，k∈Z，则称θ与φ广义互余．若sin(π＋α)＝－eq \f(1,4)，则下列角β中，可能与角α广义互余的有( )
A．sin β＝eq \f(\r(15),4) B．cs(π＋β)＝eq \f(1,4)
C．tan β＝eq \r(15) D．tan β＝eq \f(\r(15),5)
16．在角θ1，θ2，θ3，…，θ29的终边上分别有一点P1，P2，P3，…，P29，如果点Pk的坐标为(sin(15°－k°)，sin(75°＋k°))，1≤k≤29，k∈N，则cs θ1＋cs θ2＋cs θ3＋…＋cs θ29＝________.
公式
一
二
三
四
五
六
角
2kπ＋α(k∈Z)
π＋α
－α
π－α
eq \f(π,2)－α
eq \f(π,2)＋α
正弦
sin α
－sin α
－sin α
sin α
cs α
cs α
余弦
cs α
－cs α
cs α
－cs α
sin α
－sin α
正切
tan α
tan α
－tan α
－tan α
口诀
奇变偶不变，符号看象限