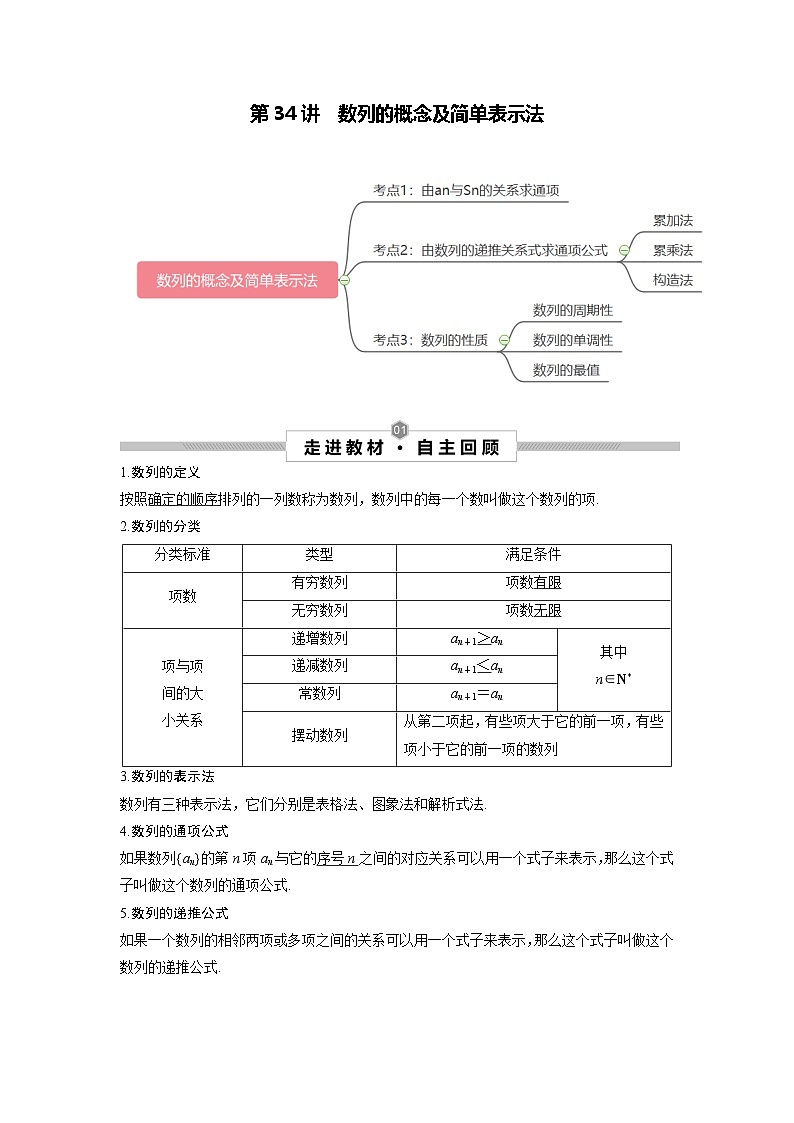
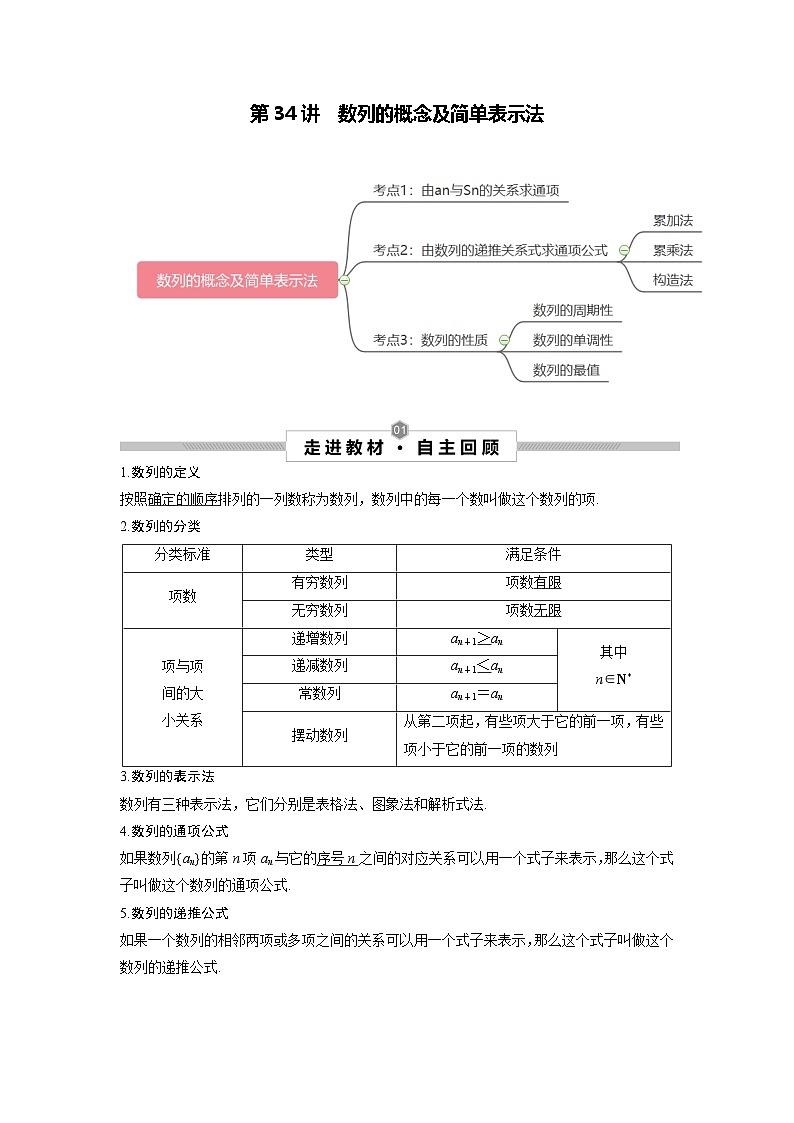
第34讲 数列的概念及简单表示法--2025高考数学一轮单元综合复习与测试卷

这是一份第34讲 数列的概念及简单表示法--2025高考数学一轮单元综合复习与测试卷，文件包含第34讲数列的概念及简单表示法原卷版docx、第34讲数列的概念及简单表示法解析版docx等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。

1.数列的定义
按照确定的顺序排列的一列数称为数列，数列中的每一个数叫做这个数列的项.
2.数列的分类
3.数列的表示法
数列有三种表示法，它们分别是表格法、图象法和解析式法.
4.数列的通项公式
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示，那么这个式子叫做这个数列的通项公式.
5.数列的递推公式
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示，那么这个式子叫做这个数列的递推公式.
考点1 由an与Sn的关系求通项
[名师点睛]
(1)已知Sn求an的常用方法是利用an＝eq \b\lc\{(\a\vs4\al\c1(S1，n＝1，,Sn－Sn－1，n≥2，))转化为关于an的关系式，再求通项公式.
(2)Sn与an关系问题的求解思路
方向1：利用an＝Sn－Sn－1(n≥2)转化为只含Sn，Sn－1的关系式，再求解.
方向2：利用Sn－Sn－1＝an(n≥2)转化为只含an，an－1的关系式，再求解.
[典例]
1.(多选)设Sn是数列{an}的前n项和，且a1＝－1，an＋1＝SnSn＋1，则下列结论正确的是( )
A.an＝eq \f(1,n（n－1）) B.an＝eq \b\lc\{(\a\vs4\al\c1(－1，n＝1，,\f(1,n（n－1）)，n≥2))
C.Sn＝－eq \f(1,n) D.数列eq \b\lc\{\rc\}(\a\vs4\al\c1(\f(1,Sn)))是等差数列
2.设数列{an}的前n项和为Sn，数列{Sn}的前n项和为Tn，满足Tn＝2Sn－n2，n∈N＋.
①求a1的值；
②求数列{an}的通项公式.
[举一反三]
1.已知数列{an}中，Sn是其前n项和，且Sn＝2an＋1，则数列的通项公式an＝________.
2.设数列{an}满足a1＋3a2＋…＋(2n－1)an＝2n，则an＝________.
考点2 由数列的递推关系式求通项公式
[名师点睛]
(1)形如an＋1＝an＋f(n)的递推关系式利用累加法求和，特别注意能消去多少项，保留多少项.
(2)形如an＋1＝an·f(n)的递推关系式可化为eq \f(an＋1,an)＝f(n)的形式，可用累乘法，也可用an＝eq \f(an,an－1)·eq \f(an－1,an－2)·…·eq \f(a2,a1)·a1代入求出通项.
(3)形如an＋1＝pan＋q的递推关系式可以化为(an＋1＋x)＝p(an＋x)的形式，构成新的等比数列，求出通项公式，求变量x是关键.
(4)形如an＋1＝eq \f(Aan,Ban＋C)(A，B，C为常数)的数列，可通过两边同时取倒数的方法构造新数列求解.
[典例]
1.在数列{an}中，a1＝2，an＋1＝an＋lneq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(1,n)))，则an等于( )
A.2＋ln n B.2＋(n－1)ln n
C.2＋nln n D.1＋n＋ln n
2.在数列{an}中，an＋1＝eq \f(n,n＋2)an(n∈N*)，且a1＝4，则数列{an}的通项公式an＝________.
3.若a1＝1，an＋1＝2an＋3，则通项公式an＝________.
4.(2022·广州调考)设数列{an}的前n项和为Sn，已知a1＝1，Sn＋1－2Sn＝1，n∈N*，则数列{an}的通项公式为________.
[举一反三]
1．（2022·河南·高三开学考试（文））在数列中，，，则（ ）．
A．659B．661C．663D．665
2．（2022·全国·高三专题练习）数列满足：，，则的通项公式为_____________.
3.已知数列{an}中，a1＝3，且点Pn(an，an＋1)(n∈N＋)在直线4x－y＋1＝0上，则数列{an}的通项公式an＝________.
考点3 数列的性质
[名师点睛]
1.解决数列周期性问题，根据给出的关系式求出数列的若干项，通过观察归纳出数列的周期，进而求出有关项的值或前n项和.
2.求数列最大项与最小项的常用方法
(1)函数法：利用相关的函数求最值.若借助通项的表达式观察出单调性，直接确定最大(小)项，否则，利用作差法.
(2)利用eq \b\lc\{(\a\vs4\al\c1(an≥an－1，,an≥an＋1))(n≥2)确定最大项，利用eq \b\lc\{(\a\vs4\al\c1(an≤an－1，,an≤an＋1))(n≥2)确定最小项.
[典例]
1．（2022·全国·高三专题练习）已知数列中，，，，则（ ）
A．4B．2C．-2D．-4
2.已知数列{an}的通项公式为an＝eq \f(3n＋k,2n)，若数列{an}为递减数列，则实数k的取值范围为( )
A.(3，＋∞) B.(2，＋∞)
C.(1，＋∞) D.(0，＋∞)
3.（2022·湖北·高三开学考试）记数列的前项和为，若，则使得取得最小值时的值为________.
[举一反三]
1.（2022·重庆·三模）已知数列的前项和为，，则（ ）
A．B．0C．D．
2.（2022·浙江·模拟预测）已知数列{}满足，则（ ）
A．B．C．D．
3.（2022·福建·莆田八中高三开学考试）已知数列满足：①先单调递减后单调递增：②当时取得最小值．写出一个满足条件的数列的通项公式_________．
4.已知数列{an}中，an＝1＋eq \f(1,a＋2（n－1）)(n∈N*，a∈R且a≠0).
(1)若a＝－7，求数列{an}中的最大项和最小项的值；
(2)若对任意的n∈N*，都有an≤a6成立，求a的取值范围.
分类标准
类型
满足条件
项数
有穷数列
项数有限
无穷数列
项数无限
项与项
间的大
小关系
递增数列
an＋1＞an
其中
n∈N*
递减数列
an＋1＜an
常数列
an＋1＝an
摆动数列
从第二项起，有些项大于它的前一项，有些项小于它的前一项的数列