

数学基础模块 下册第7章 简单几何体7.1 多面体优质课件ppt
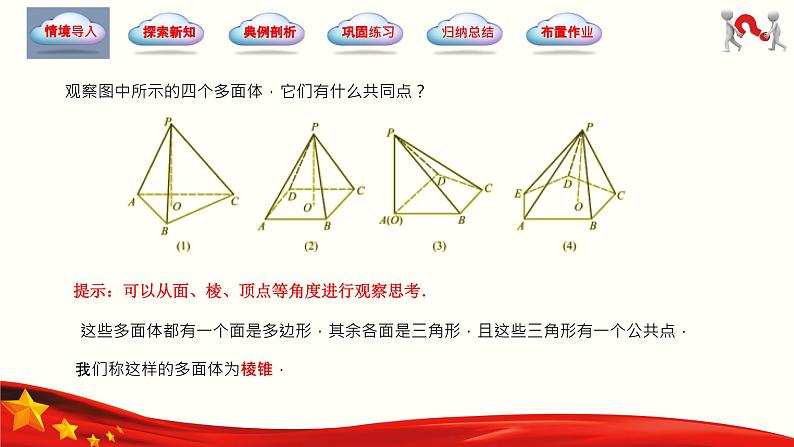
展开这些多面体都有一个面是多边形,其余各面是三角形,且这些三角形有一个公共点.
观察图中所示的四个多面体,它们有什么共同点?
我们称这样的多面体为棱锥.
提示:可以从面、棱、顶点等角度进行观察思考.
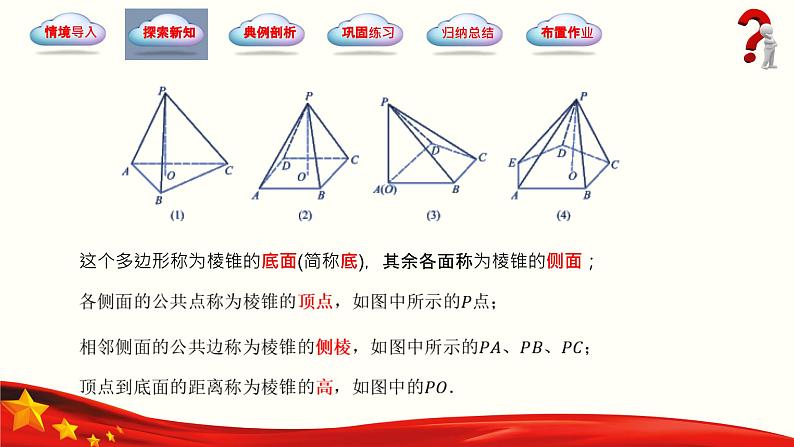
这个多边形称为棱锥的底面(简称底),其余各面称为棱锥的侧面;
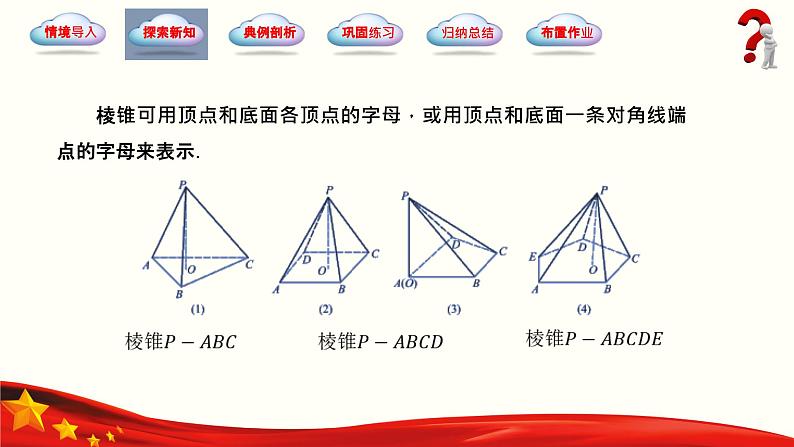
棱锥可用顶点和底面各顶点的字母,或用顶点和底面一条对角线端点的字母来表示.
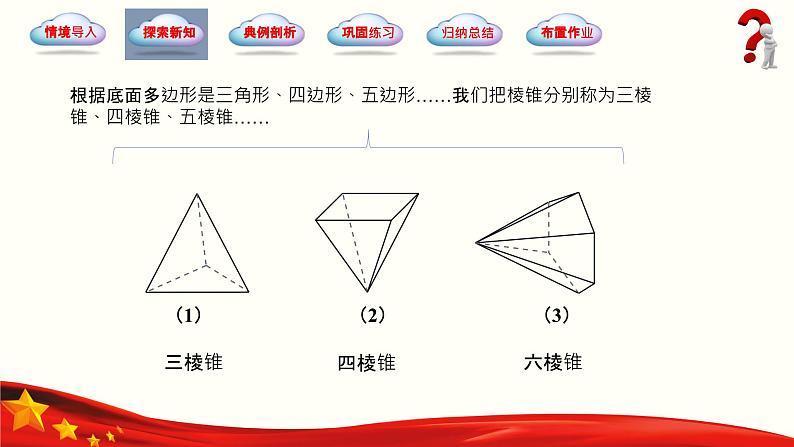
根据底面多边形是三角形、四边形、五边形……我们把棱锥分别称为三棱锥、四棱锥、五棱锥……
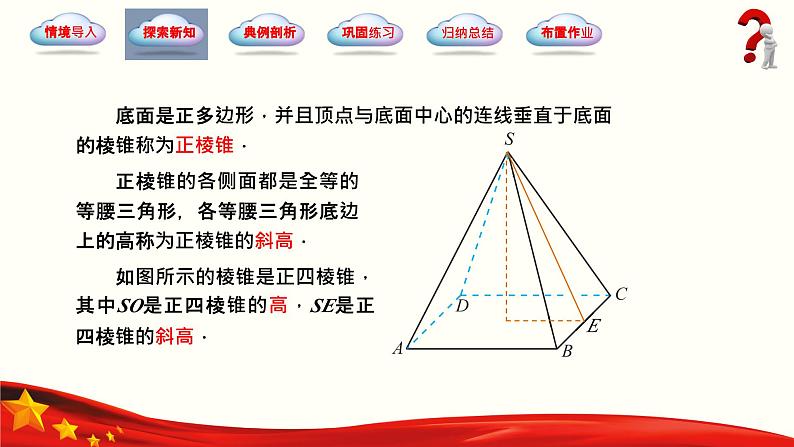
底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥称为正棱锥.
正棱锥的各侧面都是全等的等腰三角形,各等腰三角形底边上的高称为正棱锥的斜高.
如图所示的棱锥是正四棱锥,其中SO是正四棱锥的高,SE是正四棱锥的斜高.
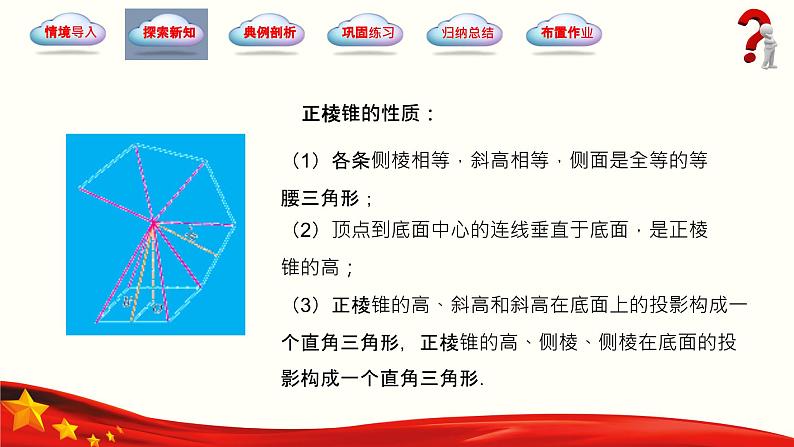
(2)顶点到底面中心的连线垂直于底面,是正棱锥的高;
(1)各条侧棱相等,斜高相等,侧面是全等的等腰三角形;
(3)正棱锥的高、斜高和斜高在底面上的投影构成一个直角三角形,正棱锥的高、侧棱、侧棱在底面的投影构成一个直角三角形.
如图,正棱锥的侧面展开图是由若干个全等的等腰三角形构成的,这些三角形的面积和就是正棱锥的侧面积.
设正棱锥的底面周长为c,斜高为h,它的侧面积公式为:
正棱锥的表面积等于它的侧面积与底面积之和.
S表面积= S侧面积+S底面积
实验用具:同底等高的正三棱柱和正三棱锥容器,如图所示,水或细沙.
(1)在正三棱锥容器中装满水或细沙;
(2)将正三棱锥容器中的水或细沙全部倒入正三棱柱容器中;
(3)重复步骤(1)(2)两次.
实验结果:水或细沙刚好注满正三棱柱容器.
实验结论:正三棱柱体积是同底等高的正三棱锥体积的3倍.
典例1 一个正四棱锥 S-ABCD 的高 SO 和底面边长都是4,如图,求它的表面积.
解 过点 O 作 OE BC 于点 E,连接SE.
又因为S底面积=4×4=16,
典例2 如图,棱锥的底面ABCD是一个矩形,AC与BD交于点M,VM是棱锥的高.若VM=4 cm,AB=4 cm,VC=5 cm,求锥体的体积.
观察棱柱与棱锥的形状,可以发现,当棱柱的一个底面保持不变,另一个底面收缩为一个点时,棱柱就变成了棱锥,棱柱的侧面从平行四边形变成了三角形.当正棱柱的一个底面收缩为一个点时,得到什么样的棱锥?棱锥侧面是什么三角形?
得到正棱锥,侧面是等腰三角形
【巩固1】已知棱长均为5,底面为正方形的四棱锥S-ABCD如图所示,求它的侧面积、表面积.
【巩固2】已知正四棱锥S-ABCD的棱长都是2,求该棱锥的体积.
解 如图,设AC,BD交于点O,连接SO,则SO是棱锥的高.
中职数学高教版(2021·十四五)基础模块 下册7.2 旋转体试讲课ppt课件: 这是一份中职数学高教版(2021·十四五)基础模块 下册<a href="/sx/tb_c4036617_t3/?tag_id=26" target="_blank">7.2 旋转体试讲课ppt课件</a>,共14页。PPT课件主要包含了圆柱的性质等内容,欢迎下载使用。
数学基础模块 上册3.1 函数的概念一等奖课件ppt: 这是一份数学基础模块 上册<a href="/sx/tb_c4036584_t3/?tag_id=26" target="_blank">3.1 函数的概念一等奖课件ppt</a>,文件包含31函数的概念同步课件pptx、31函数的概念mp4等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
中职数学2.2 区间试讲课ppt课件: 这是一份中职数学<a href="/sx/tb_c4036578_t3/?tag_id=26" target="_blank">2.2 区间试讲课ppt课件</a>,文件包含22区间同步课件pptx、22区间的概念mp4等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。












