2023-2024学年广东省惠州市惠城区知行学校七年级（下）期末数学试卷（含答案）

这是一份2023-2024学年广东省惠州市惠城区知行学校七年级（下）期末数学试卷（含答案），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.在−1，− 2，0，−2这四个数中，最小的数是( )
A. −1B. − 2C. 0D. −2
2.下列等式正确的是( )
A. 9=3B. ± 9=3C. −9=−3D. ± −9=±3
3.下列四个图形中，不能通过其中一个四边形平移得到的是( )
A. B.
C. D.
4.以下调查中，最适宜采用普查方式的是( )
A. 检测某批次汽车的抗撞击能力
B. 调查全国中学生视力和用眼卫生情况
C. 调查黄河的水质情况
D. 检查我国“神舟十三号”飞船各零部件的情况
5.如图，把一块含有30°角的直角三角板的两个锐角顶点放在直线a，b上，若a//b，∠1=67°，则∠2的度数为( )
A. 137°
B. 127°
C. 123°
D. 113°
6.若a>b，则下列不等式不成立的是( )
A. a−3>b−3B. −3a>−3bC. 1−ab3
7.一种饮料有两种包装，5大盒、3小盒共装150瓶，2大盒、6小盒共装100瓶，大盒与小盒每盒各装多少瓶？设大盒装x瓶，小盒装y瓶，则可列方程组( )
A. 5x+2y=1503x+6y=100B. 5x+2y=1503y+6x=100
C. 5x+3y=1502y+6x=100D. 5x+3y=1502x+6y=100
8.不等式2x+13+1>ax−13的解集是x5B. a=5C. a>−5D. a=−5
9.在平面直角坐标系中，将点P(m−1,n+2)向右平移3个单位，再向上平移2个单位，得到点Q.若点Q位于第二象限，则m，n的取值范围是( )
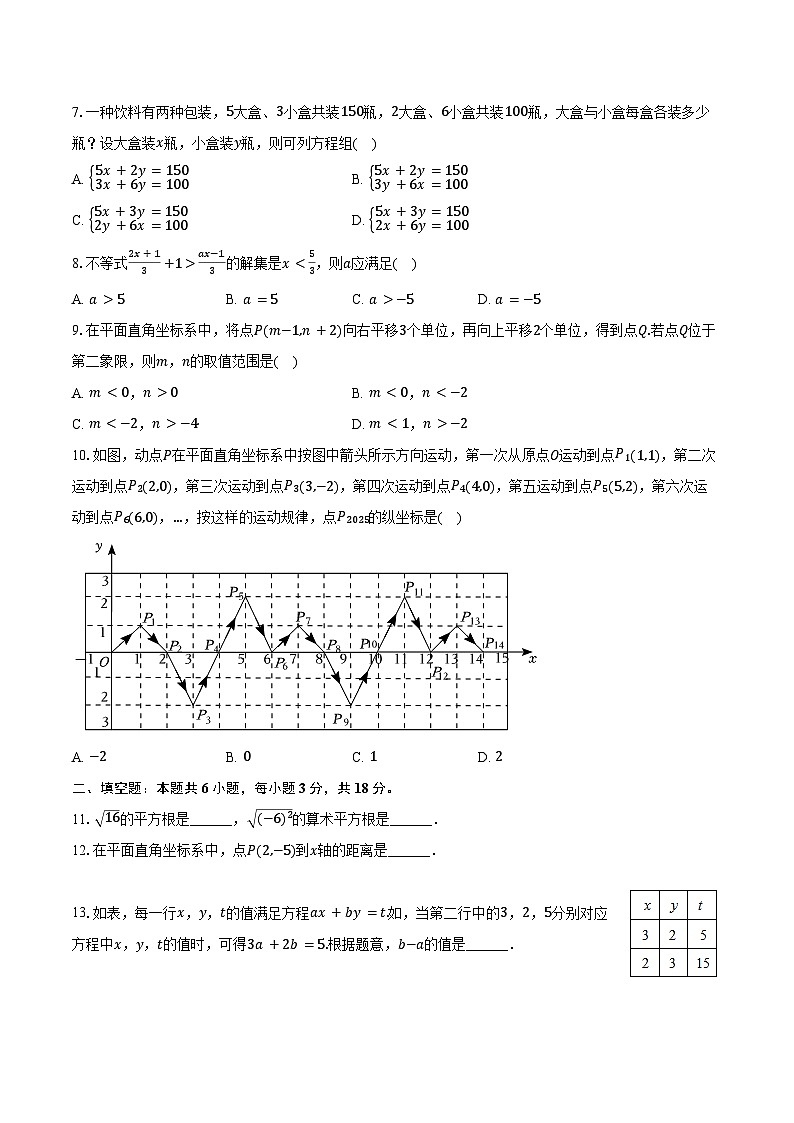
A. m0B. m−1，请求常数“□”的取值范围．
22.(本小题10分)
超市购进A、B两种商品，购进4件A种商品比购进5件B种商品少用10元，购进20件A种商品和10件B种商品共用去160元．
(1)求A、B两种商品每件进价分别是多少元？
(2)若该商店购进A、B两种商品共200件，都标价10元出售，售出一部分商品后降价促销，以标价的八折售完所有剩余商品，以10元售出的商品件数比购进A种商品的件数少30件，该商店此次销售A、B两种商品共获利不少于640元，求至少购进A种商品多少件？
23.(本小题10分)
【发现】如图1，直线AB，CD被直线EF所截，EM平分∠AEF，FM平分∠CFE.若∠AEM=55°，∠CFM=35°，试判断AB与CD平行吗？并说明理由；
【探究】如图2，若直线AB//CD，点M在直线AB，CD之间，点E，F分别在直线AB，CD上，∠EMF=90°，P是MF上一点，且EM平分∠AEP.若∠CFM=60°，则∠AEP的度数为______；
【延伸】若直线AB//CD，点E，F分别在直线AB，CD上，点M在直线AB，CD之间，且在直线EF的左侧，P是折线E−M−F上的一个动点，∠EMF=90°保持不变，移动点P，使EM平分∠AEP或FM平分∠CFP.设∠CFP=α，∠AEP=β，请直接写出α与β之间的数量关系．
24.(本小题12分)
如图1，在平面直角坐标系中，点A、B在坐标轴上，其中A(0,a).B(b,0)，且满足|a−3|+ b−4=0．
(1)求A、B两点的坐标；
(2)将线段AB平移到CD.点A的对应点是C(−4.0).点B的对应点是D.且C、D两点也在坐标轴上，过点O作直线OM⊥AB，垂足为M，交CD于点N.请在图1中画出图形，直接写出点D的坐标，并证明MN⊥CD；
(3)如图2，将AB平移到CD、点A对应点C(−2,m)，连接AC、BC.BC交y轴于点E，若△ABC的面积等于12，求点E的坐标及m的值．
参考答案
1.D
2.A
3.D
4.D
5.B
6.B
7.D
8.B
9.C
10.A
11.±2 6
12.5
13.10
14.5≤ax−4，
∴x>2，
∴不等式组的解集为x>2；
(2)2x−4x−42，
设常数“□”为m，
∵x−m>x−42，
∴2x−2m>x−4，
∴x>2m−4，
∴不等式x−m>x−42的解集为x>2m−4，
又∵不等式2x−4−1，
而不等式组2x−4x−42的解集为x>−1，
∴−1≥2m−4，
∴m≤32，
∴□≤32．
22.(1)设A甲种商品每件进价x元，B乙种商品每件进价y元，
根据题意，得5y−4x=1020x+10y=160，解得：x=5y=6，
答：A种商品每件进价5元，B种商品每件进价6元．
(2)设A种商品购进a件，则乙种商品(200−a)件，
根据题意，得10(a−30)+0.8×10[200−(a−30)]−5a−6(200−a)≥640，
解得：a≥100，
答：至少购进A种商品100件．
23.60°
【解析】解：[发现]平行，理由是：
∵∠AEM=55°，EM平分∠AEF，
∴∠AEF=2∠AEM=110°，
∵∠CFM=35°，FM平分∠CFE，
∴∠CFE=2∠CFM=70°，
∴∠AEF+∠CFE=180°，
∴AB//CD；
[探究]如图，过M作MN//AB，
∵AB//CD，
∴AB//CD//MN，
∴∠AEM=∠NME，∠CFM=∠NMF=60°，
∴∠EMF=∠EMN+∠FMN=∠AEM+∠CFM=90°，
∵∠NMF=60°，
∴∠AEM=∠EMN=30°，
∵EM平分∠AEP，
∴∠AEP=2∠AEM=60°；
[延伸]如图，若EM平分∠AEP，
∴∠AEM=∠PEM=12β，
同上可得：∠M=∠AEM+∠CFM=90°，
∴∠CFP=90°−∠AEM，
∴α=90°−12β，即α+12β=90°；
若FM平分∠CFP，
∴∠CFM=∠PFM=12∠CFP=12α，
同上可得：∠M=∠AEM+∠CFM=90°，
∴β+12α=90°；
综上：α与β之间的数量关系为α+12β=90°或β+12α=90°．
24.解：(1)∵|a−3|+ b−4=0，
∴a−3=0，且b−4=0，
∴a=3，b=4，
∴点A的坐标为(0,3)，点B的坐标为(4,0)；
(2)如图1，由平移的性质可知：AB/​/CD，AB=CD，
∴∠ABO=∠DCO，
∵OM⊥AB，
∴OM⊥CD，
即MN⊥CD．
在△AOB和△DOC中，
∠AOB=∠DOC∠ABO=∠DCOAB=DC，
∴△AOB≌△DOC(AAS)，
∴OA=OD=3，
∴D(0,−3)．
(3)如图2，过点C作CF⊥y轴于点F，
由(1)可知，A、B两点的坐标为(0,3)，(4,0)，
∴OA=3，OB=4，
∵点C的坐标为(−2,m)，
∴CF=2，OF=−m，
∵△ABC的面积等于12，
∴S△ACE+S△ABE=12，
∴12AE⋅CF+12AE⋅OB=12，
即12(3+OE)×2+12×(3+OE)×4=12，
解得：OE=1，
∴点E的坐标为(0,−1)．
过B作BG⊥CF于G，过A作AH⊥BG于H，
则AH//CG，OF=BG，AH=FG=OB=4，BH=OA=3，
∴CG=CF+FG=6，
∵△ABC的面积等于12，
∴S梯形AHGC−S△ABH−S△BCG=S△ABC=12，
即12×(4+6)×(3+OF)−12×3×4−12×6⋅OF=12，
解得：OF=32，
∴−m=32，
∴m=−32，
即点E的坐标为(0,−1)，m的值为−32． 组别
作业时间
人数
A
0≤x