厦门外国语学校2023-2024学年高一下学期期中考试数学试卷(含答案)

这是一份厦门外国语学校2023-2024学年高一下学期期中考试数学试卷(含答案)，共22页。试卷主要包含了选择题，多项选择题，填空题，双空题，解答题等内容，欢迎下载使用。

一、选择题
1．已知i为虚数单位若复数,则z的虚部是( )
A.1B.-1C.iD.
2．水平放置的的直观图如图所示,是中边的中点,且平行于轴,则,,对应于原中的线段AB,AD,AC,对于这三条线段,正确的判断是( )
A.最短的是ADB.最短的是ACC.D.
3．在中，角A，B，C所对边分别为a，b，c，且，，，( )
A.B.或C.D.或
4．设m,n是两条不同的直线,,是两个不同的平面,则下列命题中正确的是( )
A.若,,则B.若,,则
C.若,,则D.若,,则
5．中,a、b、c分别是内角A、B、C的对边,若且,则形状是( )
A.有一个角是的等腰三角形B.顶角是的等腰三角形
C.等腰直角三角形D.不能确定三角形的形状
6．已知向量,,若向量在向量上的投影向量,则( )
A.7B.C.D.
7．如图,在直三棱柱中,,P为线段的中点,Q为线段（包括端点）上一点,则的面积的最大值为( )
A.B.C.2D.
8．已知平面向量,满足,,则的最大值为( )
A.2B.C.D.3
二、多项选择题
9．已知z是复数,是其共轭复数,则下列命题中错误的是( )
A.
B.若,则的最大值为
C.若,则复平面内对应的点位于第一象限
D.若是关于x的方程的一个根,则
10．已知的内接四边形中,,,下列说法正确的是( )
A.B.四边形的面积为
C.该外接圆的直径为D.
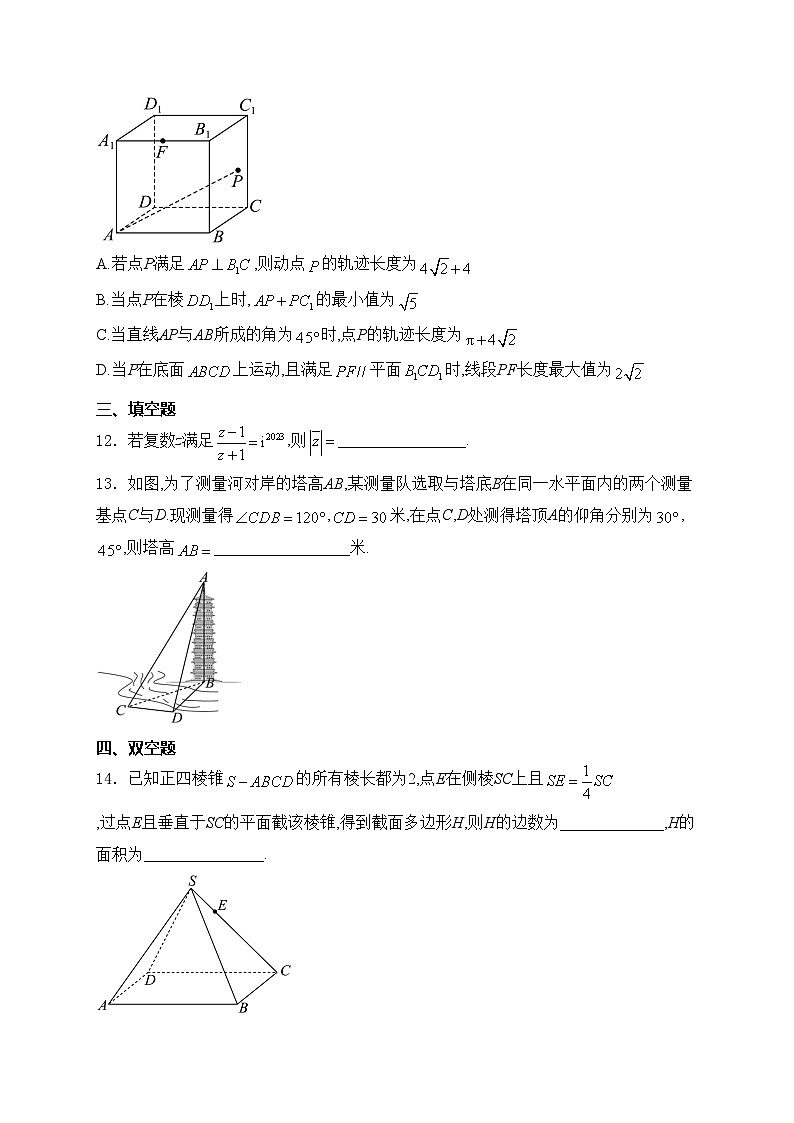
11．如图,点P是棱长为2的正方体的表面上一个动点,F是线段的中点,则( )
A.若点P满足,则动点的轨迹长度为
B.当点P在棱上时,的最小值为
C.当直线AP与AB所成的角为时,点P的轨迹长度为
D.当P在底面上运动,且满足平面时,线段PF长度最大值为
三、填空题
12．若复数z满足,则________________.
13．如图,为了测量河对岸的塔高AB,某测量队选取与塔底B在同一水平面内的两个测量基点C与D.现测量得,米,在点C,D处测得塔顶A的仰角分别为,,则塔高_________________米.
四、双空题
14．已知正四棱锥的所有棱长都为2,点E在侧棱SC上且,过点E且垂直于SC的平面截该棱锥,得到截面多边形H,则H的边数为_____________,H的面积为_______________.
五、解答题
15．如图,在中,,点E为中点,点F为上的三等分点,且靠近点C,设.
(1)用,表示,;
(2)如果,,且,求.
16．记的内角A,B,C的对边分别为a,b,c,已知.
(1)求角A的大小;
(2)若D点在线段BC上,且AD平分,若,且,求a.
17．如图,四棱锥的侧面是边长为2的正三角形,底面为矩形,且平面平面,M,N分别为,的中点,直线PC与面所成角的正切值为.
(1)证明：平面;
(2)证明：.
18．在中,角A,B,C所对的边分别为a,b,c,请从下列条件中选择一个条件作答：①
②
③
(1)求A的大小
(2)若为锐角三角形,求的取值范围;
(3)若,点A,B,C分别在等边的边DE,EF,FD上（不含端点）,若面积的最大值为,求c.
19．如图,在矩形中,,,M是线段AD上的一动点,将沿着BM折起,使点A到达点的位置,满足点平面且点在平面内的射影E落在线段BC上.
(1)当点M与端点D重合时,证明：平面;
(2)当时,求二面角的余弦值;
(3)设直线CD与平面所成的角为,二面角的平面角为,求的最大值.
参考答案
1．答案：A
解析：因为复数,
所以z的虚部是1,
故选：A.
2．答案：A
解析:因为平行于轴,所以在中,,
又因为是中边的中点,所以D是BC的中点,
所以.
故选:A
3．答案：A
解析：由正弦定理有，即，解得，
注意到，由大边对大角有，所以
故选：A.
4．答案：C
解析：如图所示
对于A,设平面为平面,平面为平面,m为,则,,则,故A错;
对于B,设平面为平面,平面为平面,m为,则,,则,故B错;
对于C,过m作平面与平面交于直线b,,则,,可得,则,故C正确;
对于D,设平面为平面,为m,为n,则,,则,故D错.
故选：C.
5．答案：C
解析：如图所示,在边、上分别取点D、E,使、,
以、为邻边作平行四边形,则,显然,
因此平行四边形为菱形,平分,而,则有,即,
于是得是等腰三角形,即,令直线交于点O,则O是边的中点,,
而,因此有,从而得,
所以是等腰直角三角形.
故选：C
6．答案：D
解析：由题意可得,向量在向量上的投影向量为,
则,解得,则,,
故.
故选：D.
7．答案：A
解析：取AB的中点E,连接CE,过Q作,垂足为M,
过M作,垂足为N,连接QN,PE,
则,且,点E到BC的距离为.
由直三棱柱的性质知平面ABC,
所以平面ABC,MN,平面ABC,
则,,且,QM,平面QMN,
所以平面QMN,且平面QMN,
则,可知,
当且仅当点Q与点P重合时,等号成立,
所以面积的最大值为.
故选：A.
8．答案：C
解析：设,,如图,
由题意,即在平行四边形中,,,
求的最大值.
延长至,使,则,
由正弦定理,O,A,C三点所在外接圆的直径,
所以,设圆心为G,如图,
所以可知,又,,
所以由余弦定理可得,
则由图象可知,
故选：C.
9．答案：ACD
解析：设,则,其中a,,
A：,,故故A错误;
B：因为,由复数的几何意义可知复数对应的点在以原点为圆心的单位圆上,
而表示圆上的点到点的距离,又圆心到的距离为,
所以圆上的点到的最大距离为,故B正确;
C：因为,所以,复平面内对应的点位于第二象限,故C错误;
D：是关于x的方程的一个根,
所以,整理可得,
所以,解得,,故D错误;
故选：ACD.
10．答案：ABD
解析：在的内接四边形中,连接,,,,,
对于A,由余弦定理得,,
即,解得,而,则,A正确;
对于B,,四边形的面积,B正确;
对于C,由选项A知,,
由正弦定理得的半径,C错误;
对于D,取中点E,连接,则,,
同理,所以,D正确.
故选：ABD.
11．答案：ACD
解析：对于A,易知平面,平面,故动点P的轨迹为矩形,
动点P的轨迹长度为矩形的周长,即为,故A正确;
对于B,以为轴将平面顺时针旋转,如图,
则,故B错误;;
对于C：连接AC,,以B为圆心,为半径画弧,如图1所示,
当点P在线段,和弧上时,直线与所成的角为,
又,
弧长度,故点P的轨迹长度为,故C正确;
对于D,取,,,,,的中点分别为O,R,N,M,T,H,
连接,,,,,,,,如图2所示,
因为,平面,平面,故平面,
,平面,平面,故平面;
又,,平面,故平面平面;
又,,
故平面与平面是同一个平面.
则点P的轨迹为线段：
在三角形中,
则,
故三角形是以为直角的直角三角形;
故,故长度的最大值为,故D正确.
故选：ACD.
12．答案：1
解析：由复数,可得,所以,可得.
故答案为：1.
13．答案：30米
解析：在直角中,因为,可得,
在直角中,因为,可得,
在中,因为,,
由余弦定理得,
即,可得,
解得或（舍去）,即塔的高度为米.
故答案为：30米.
14．答案：5;
解析：取中点F,,且,,平面,
可知平面,
根据平面的基本性质,作平面与平面平行,如图为五边形.
因为,所以,则,,
可得,,
则,可得,
所以,
又因为与的夹角为与夹角,而与垂直,
易知且,,即为矩形,则,
可得,
故答案为：5; .
15．答案：(1),
(2)
解析：(1)因为,
所以,
;
(2)因为,所以,
所以,由,可得,
又,所以,
所以.
16．答案：(1)
(2)
解析：(1)由正弦定理可得,
所以,
即,
可得,
整理可得,
因为在中,,
所以,又,
所以;
(2)因为,AD平分,
所以,
由得,
即,整理可得,①
因为为角平分线,所以,
在中由正弦定理可得,
在中由正弦定理可得,
又,所以,
所以,②
由①②可得,
在中,由余弦定理可得
,
解得.
17．答案：(1)证明见解析;
(2)证明见解析;
解析：(1)证明：取边中点E,连接,,
因为M,N分别为,的中点,由三角形中位线的性质可得,
平面,所以平面,
又底面为矩形,所以且相等,
所以四边形为平行四边形,所以,
平面,所以平面,
因为,,平面,又,,平面,
所以平面平面,
又平面,
所以平面.
(2)取中点N,连接,,,
因为侧面是边长为2的正三角形,所以,
又平面平面,平面平面,
所以平面,
又平面,
所以,即为直线PC与面所成的线面角,
又直线PC与面所成角的正切值为,
所以,
,,
所以,
又,所以底面为正方形,
平面,所以
在正方形中,易得,
,
而,
,,
,且,平面,
平面,
因为平面,
18．答案：(1)
(2)
(3)
解析：(1)选择①：
因为,
所以,
化简可得,
由正弦定理可得,
由余弦定理可得,
又,
所以.
选②：
因为,
由正弦定理可得,
所以,
又,,
可得,
解得或（舍去）,
因为,,可得,
所以;
选③：
因为,且,
所以,即,
由正弦定理可得,
又,
所以,
因为,所以,
又,
所以.
(2)由正弦定理可得,
由(1)可得,所以,
因为为锐角三角形,
所以,
所以,
所以,
即的取值范围为.
(3)由（1）可得,,因为面积的最大值为,
则,所以的最大值为,
因为,所以,
因为,所以,
设,
则,
在中,由正弦定理可得,
所以,可得,
在中,由正弦定理得,
所以,
所以
,
其中,
所以当时,取得最大值,
所以,即,
所以,
解得或（舍去）.
19．答案：(1)证明见解析
(2)
(3)
解析：(1)当点M与端点D重合时,由可知,
由题意知平面,平面,所以,
又,,平面,平面,
所以平面,又平面,可知
,平面,平面,
所以平面.
(2)作于,连接,,
由题意,折起后由题意可得,平面,
因为平面,所以,
又,,平面,
所以平面,
所以A,O,E三点共线,
所以为二面角的平面角,
因为,,
在中,,
由三角形面积相等可得
又因为,所以,即,
所以在中,,
即二面角的余弦值为.
(3)过点E做交于Q,所以直线与平面所成的角即为直线与平面所成的角,
由(2)可知平面,平面,所以平面平面,
作,垂足为H,平面平面,平面,可得平面,
连接,是直线与平面所成的角,即,
因为,满足,
设,,,,,
,
因为在中,斜边大于直角边,即,
所以,所以,
,
在中由等面积,,
因为,,所以是二面角平面角,
即,,
,当且仅当时“＝”成立,
故的最大值为.