2025高考数学一轮复习第2章基本初等函数11第12讲函数与方程（课件+解析试卷）

这是一份2025高考数学一轮复习第2章基本初等函数11第12讲函数与方程（课件+解析试卷），文件包含第2章基本初等函数11第12讲函数与方程pptx、第2章基本初等函数11第12讲函数与方程docx等2份课件配套教学资源，其中PPT共59页， 欢迎下载使用。
1．(人A 必一P155T1改编)下列函数图象与x轴都有公共点，其中不能用二分法求图中函数零点近似值的是(　　)
　　　　根据题意，利用二分法求函数零点的条件是函数在零点的左右两侧的函数值符号相反，即穿过x轴．据此分析知A选项中函数不能用二分法求零点．
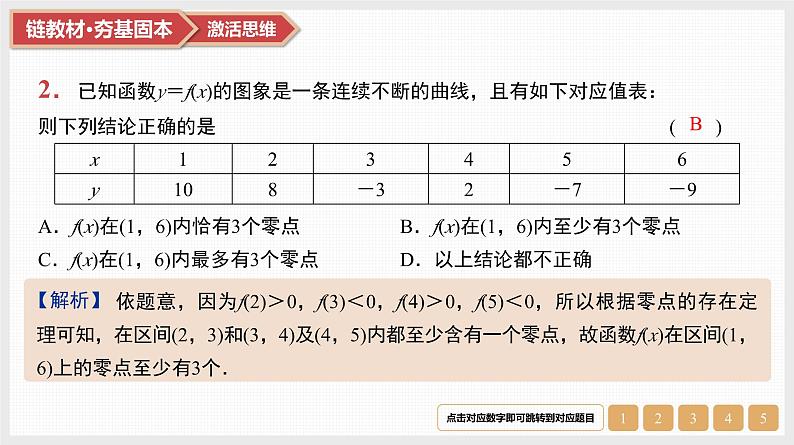
2．已知函数y＝f(x)的图象是一条连续不断的曲线，且有如下对应值表：则下列结论正确的是(　　)A．f(x)在(1，6)内恰有3个零点B．f(x)在(1，6)内至少有3个零点C．f(x)在(1，6)内最多有3个零点D．以上结论都不正确
　　　　依题意，因为f(2)＞0，f(3)＜0，f(4)＞0，f(5)＜0，所以根据零点的存在定理可知，在区间(2，3)和(3，4)及(4，5)内都至少含有一个零点，故函数f(x)在区间(1，6)上的零点至少有3个．
4．(人A 必一P160T5(3))已知函数f(x)＝2x＋x，g(x)＝lg2x＋x，h(x)＝x3＋x的零点分别为a，b，c，则a，b，c的大小顺序为(　　)A．a＞b＞cB．b＞c＞aC．c＞a＞bD．b＞a＞c
　　　　由h(x)＝x3＋x＝0得x＝0，所以c＝0．由f(x)＝0得2x＝－x，由g(x)＝0得lg2x＝－x．在同一平面直角坐标系中画出y＝2x，y＝lg2x，y＝－x的图象如图所示．由图象知a＜0，b＞0，所以a＜c＜b．
　　　　作出f(x)的图象如图所示．方程f(x)＝k(k＜0)的实数解的个数等于直线y＝k与y＝f(x)图象的交点个数．
1．函数的零点与方程的解(1)函数零点的概念对于一般函数y＝f(x)，我们把使_____________的实数x叫做函数y＝f(x)的零点．(2)函数零点与方程实数解的关系方程f(x)＝0有实数解⇔函数y＝f(x)有________⇔函数y＝f(x)的图象与________有公共点．(3)函数零点存在定理如果函数y＝f(x)在区间[a，b]上的图象是一条连续不断的曲线，且有___________，那么，函数y＝f(x)在区间____________内至少有一个零点，即存在c∈(a，b)，使得_____________，这个c也就是方程f(x)＝0的解．
f(a)f(b)＜0　
2．二分法对于在区间[a，b]上图象连续不断且______________的函数y＝f(x)，通过不断地把它的零点所在区间一分为二，使所得区间的两个端点逐步逼近________，进而得到零点近似值的方法叫做二分法．
　　　(1)函数f(x)＝x＋lg2x的零点所在的区间为(　　)
　　　(2)若方程x lg (x＋2)＝1的实根在区间(k，k＋1)(k∈Z)上，则k等于(　　)A．－2B．1C．－2或1D．0
确定函数零点所在区间的方法(1)利用函数零点的存在定理：首先看函数y＝f(x)在区间[a，b]上的图象是否连续，再看是否有f(a)·f(b)＜0，若有，则函数y＝f(x)在区间(a，b)内必有零点．(2)数形结合法：通过画函数图象，观察图象与x轴在给定区间上是否有交点来判断．
零点个数及参数范围的判定
　　　(1)已知函数y＝f(x)是周期为2的周期函数，且当x∈[－1，1]时，f(x)＝2|x|－1，则函数F(x)＝f(x)－|lg x|的零点个数是(　　)A．9　　　　　　B．10　　　　　　C．11　　　　　　D．18
　　　　F(x)＝f(x)－|lg x|的零点个数就是y＝f(x)与y＝|lg x|图象的交点个数．在同一平面直角坐标系中作出y＝f(x)，y＝|lg x|的图象如图所示，由图可得两函数图象有10个交点，故F(x)＝f(x)－|lg x|有10个零点．
判断函数零点个数的方法(1)解方程法：所对应方程f(x)＝0有几个不同的实数解就有几个零点．(2)零点存在定理法：利用零点存在定理并结合函数的性质进行判断．(3)数形结合法：转化为两个函数的图象的交点个数问题．先画出两个函数的图象，看其交点的个数，交点的个数就是函数零点的个数．
　　　　直线kx－y＋k＝0(k＞0)，即k(x＋1)－y＝0(k＞0)过定点(－1，0)．因为函数f(x)满足f(1－x)＝f(1＋x)，所以函数f(x)的图象关于直线x＝1对称．又因为函数f(x)为偶函数，所以函数f(x)的图象关于y轴对称．在平面直角坐标系内画出函数f(x)的图象及直线k(x＋1)－y＝0(k＞0)如图所示．
　　　(2)(2023·深圳一调)(多选)已知函数f(x)＝x(x－3)2，若f(a)＝f(b)＝f(c)，其中a＜b＜c，则(　　　)A．1＜a＜2B．a＋b＋c＝6C．a＋b＞2D．abc的取值范围是(0，4)
　　　　因为f(x)＝x(x－3)2，所以f′(x)＝3x2－12x＋9＝3(x－3)(x－1)．令f′(x)＝0，解得x＝1或x＝3，当f′(x)＞0时，x＞3或x＜1，所以f(x)的单调递增区间为(－∞，1)和(3，＋∞)；当f′(x)＜0时，1＜x＜3，所以f(x)的单调递减区间为(1，3)，且f(3)＝0，f(1)＝f(4)＝4，如图．
设f(a)＝f(b)＝f(c)＝t，则0＜t＜4，0＜a＜1＜b＜3＜c＜4，故A错误．又f(x)－t＝(x－a)(x－b)(x－c)，所以x(x－3)2－t＝(x－a)(x－b)(x－c)，即x3－6x2＋9x－t＝x3－(a＋b＋c)x2＋(ab＋ac＋bc)x－abc，对照系数得a＋b＋c＝6，故B正确．abc＝t∈(0，4)，故D正确．因为3＜c＜4，所以3＜6－(a＋b)＜4，则2＜a＋b＜3，故C正确．
(1)对于函数f(x)＝|lgax|，若存在正数m，n(m＜n)，满足f(m)＝f(n)，则0＜m＜1＜n，且mn＝1．(2)等高线问题重在“减元”，要充分利用“函数值相等”，树立目标意识，预设“消谁留谁”，利用“函数值相等”的逆向使用，探究出自变量间的等量关系．
　　　　作出f(x)的图象如图所示．由图象可得x1＋x2＝－2，x3x4＝1．
1．函数f(x)＝ex＋2x－6的零点所在的区间是(　　)A．(3，4)B．(2，3)C．(1，2)D．(0，1)
　　　　函数f(x)＝ex＋2x－6是R上的连续增函数，由f(1)＝e－4＜0，f(2)＝e2－2＞0，可得f(1)f(2)＜0，所以函数f(x)的零点所在的区间是(1，2)．
　　　　函数g(x)＝f(x)－k有两个不同的零点，即为函数y＝f(x)与直线y＝k有两个交点．作出函数y＝f(x)的图象如图所示，由图可知k∈[0，1)．
　　　　设x1＜x2＜x3，作出f(x)的大致图象如图所示．
由图知|lg2x1|＝|lg2x2|＝－x3＋3∈(0，1)，所以lg2x1＝－lg2x2，即x1x2＝1．由f(x1)＝f(x2)＝f(x3)，得x3∈(2，3)，所以x1x2x3的取值范围是(2，3)．
A组　巩固练1．函数f(x)＝2x|lg2x|－1的零点个数为(　　)A．0B．1C．2D．4
A．[－1，0)B．[0，＋∞)C．[－1，＋∞)D．[1，＋∞)
　　　　由g(x)＝0得f(x)＝－x－a，作出函数f(x)和y＝－x－a的图象如图所示．由图可知当直线y＝－x－a的截距－a≤1，即a≥－1时，直线与函数f(x)的图象有2个交点，即函数g(x)存在2个零点，故实数a的取值范围是[－1，＋∞)．
　　　　画出函数f(x)的图象如图所示．因为函数y＝f(x)－2g(x)恰有三个零点，所以f(x)＝2g(x)有三个不等实根，即f(x)的图象与y＝2g(x)＝2mx的图象有三个不同的交点．
由图可知，当m＞0时，两个函数的图象有1个交点，当m≤0时，两个函数的图象有2个交点，所以函数g(x)＝f(x)－m的零点可能有1个或2个．
6．(多选)已知定义域为R的偶函数f(x)有4个零点x1，x2，x3，x4(x1＜x2＜x3＜x4)，并且当x≥0时，f(x)＝x2－ax＋1，则下列说法正确的是(　 　)A．实数a的取值范围是(－∞，－2)∪(2，＋∞)B．当x＜0时，f(x)＝x2＋ax＋1C．x1x2x3x4＝1
当x＜0时，－x＞0，则f(x)＝f(－x)＝x2＋ax＋1，故B正确．偶函数f(x)的4个零点满足x1＜x2＜x3＜x4，则x3，x4是方程x2－ax＋1＝0的两个根， 则有x3x4＝1，又x1＝－x4，x2＝－x3，于是得x1x2x3x4＝(x3x4)2＝1，故C正确．
A．x1x2＋4＝2(x1＋x2)B．x3＋x4＝12C．x3x4∈(32，34)D．函数g(x)＝(f(x))2＋(1－m)f(x)－m的零点为6，x1，x2，x3，x4
　　　　由解析式可得f(x)的图象如图所示．
对于B，因为f(x3)＝f(x4)，所以x3与x4关于直线x＝6对称，所以x3＋x4＝12，故B正确．
对于D，g(x)＝(f(x))2＋(1－m)f(x)－m＝(f(x)－m)(f(x)＋1)，由g(x)＝0得f(x)＝m或f(x)＝－1，因为f(x)＝m的根为x1，x2，x3，x4，f(x)＝－1的根为6，所以g(x)的零点为6，x1，x2，x3，x4，故D正确．
令g(x)＝0得f(x)－3＝0，即f(x)＝3，当x＞0时，2x－5＝3，解得x＝4；当x≤0时，2x＝3，解得x＝lg23＞0(舍去)．综上，函数g(x)＝f(x)－3的零点为4．
9．若函数f(x)＝e－x－ln (x＋a)在(0，＋∞)上存在零点，则实数a的取值范围是_____________．
　　　　由题意可得函数y＝e－x与g(x)＝ln (x＋a)的图象在(0，＋∞)上有交点．
当a＞0时，g(x)＝ln (x＋a)的图象是由函数y＝ln x的图象向左平移a个单位长度得到的，由图象可得g(0)＝lna＜1，即0＜a＜e；
当a≤0时，g(x)＝ln (x＋a)的图象是由函数y＝ln x向右平移|a|个单位长度得到的，此时在(0，＋∞)上恒有交点，满足条件．综上，实数a的取值范围为(－∞，e)．
　　　　作出函数f(x)的图象如图所示．
11．已知函数f(x)＝x2－3mx＋n(m＞0)的两个零点分别为1和2．(1) 求m，n的值；
　　　　由函数f(x)＝x2－3mx＋n(m＞0)的两个零点分别为1和2，可得1－3m＋n＝0，4－6m＋n＝0，解得m＝1，n＝2．
11．已知函数f(x)＝x2－3mx＋n(m＞0)的两个零点分别为1和2．
12．(2023·杭州一检)已知函数f(x)满足f(x)＝2f(－x)＋3x－1．(1) 求函数f(x)的解析式；
　　　　由题意得f(－x)＝2f(x)－3x－1，所以f(x)＝2(2f(x)－3x－1)＋3x－1，解得f(x)＝x＋1．
12．(2023·杭州一检)已知函数f(x)满足f(x)＝2f(－x)＋3x－1．(2) 若关于x的方程|f(x)|＝k|x2－x－1|恰有四个不同的实根，求实数k的取值范围．
　　　　当k＜0时，明显无解；当k＝0时，|x＋1|＝0只有一个实根，不符合条件；