高考数学一轮复习第三章第八讲解三角形应用举例课件

这是一份高考数学一轮复习第三章第八讲解三角形应用举例课件，共34页。PPT课件主要包含了故选B答案B，答案B，答案C，解析如图D20，图D20，答案113，的小艇，图3-8-5，反思感悟，思想的应用等内容，欢迎下载使用。
能够运用正弦定理、余弦定理等知识和方法解决一些与测量
和几何计算有关的实际问题.
【名师点睛】易混淆方位角与方向角的概念
(1)方位角是指北方向线按顺时针旋转到目标方向线之间的水平夹角，而方向角是正北或正南方向线与目标方向线所成的锐角.
(2)“方位角”与“方向角”的范围：方位角大小的范围是
[0°，360°)，方向角大小的范围是[0°，90°).
考点一 距离问题[例 1](2023 年厦门市期末)一个人骑自行车由 A 地出发向正东方向骑行了 4 km 到达 B 地，然后由 B 地向南偏东 30°方向骑行了6 km 到达 C 地，再从 C 地向北偏东 30°方向骑行了 16 km 到达 D
地，则 A，D 两地的距离为(
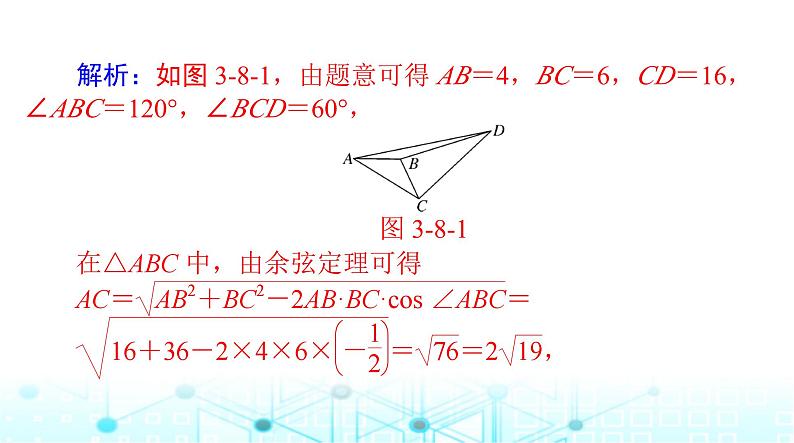
解析：如图 3-8-1，由题意可得 AB＝4，BC＝6，CD＝16，∠ABC＝120°，∠BCD＝60°，图 3-8-1
在△ACD 中，由余弦定理可得
【变式训练】(2023 年种田地区校级期末)如图 3-8-2，为了测量河对岸两点C，D 间的距离，现在沿岸相距 2 km 的两点 A，B 处分别测得∠BAC ＝105°，∠BAD＝60°，∠ABC＝45°，∠ABD＝60°，
则 C，D 间的距离为(　　)
解析：因为∠ABD＝60°，∠BAD＝60°，所以△ABD 是等边三角形，所以 AB＝BD＝DA＝2，在△ABC 中，∠ABC＝45°，∠BAC＝105°，所以∠ACB＝30°，
在△ACD 中，∠CAD＝105°－60°＝45°，
所以 CD＝2，即 C，D 间的距离为 2 km.故选 B.
考点二 测量高度问题[例 2](2023 年开封市期末)如图 3-8-3，为测量河对岸的塔高 AB，选取了与塔底 B 在同一水平面内的两
【变式训练】(2023 年东莞市校级月考)和谐钟塔位于江西省赣州市章贡区赣州大桥东岸引桥南侧，有四个直径达 12.8 米的钟面.小赵同学经过和谐钟塔时，想利用正弦定理的知识测量该钟塔的高度.如图3-8-4，他在该钟塔塔底 B 点的正西处的 C 点测得该钟塔塔顶 A 点的仰角为 30°，然后沿着东偏南67°的方向行进了 180.8 m 后到达 D 点(B，C，D三点处于同一水平面)，且 B 点在 D 点北偏东 37°的方向上，则该钟塔的高度为________m.(参考数
据：取 sin 53°≈0.8)
∠BCD＝67°，∠CDB＝90°－67°＋37°＝60°，则∠CBD＝180°－60°－67°＝53°.
[例 3]在一次海上联合作战演习中，红方一艘侦察艇发现在北偏东 45°方向，相距 12 n mile 的水面上，有蓝方一艘小艇正以每小时 10 n mile 的速度沿南偏东 75°方向前进，若红方侦察艇以每小时14 n mile 的速度，沿北偏东45°＋α方向拦截蓝方的小艇，若要在最短的时间内拦截住，求红方侦察艇所需的时间和角α的正弦值.
解：如图 3-8-5，设红方侦察艇经过 x 小时后在 C 处追上蓝方
则 AC＝14x，BC＝10x，∠ABC＝120°.
(1)测量角度问题的关键是在弄清题意的基础上，画出表示实际问题的图形，并在图形中标出有关的角和距离，再用正弦定理或余弦定理解三角形，最后将解得的结果转化为实际问题的解.(2)方向角是相对于某点而言的，因此在确定方向角时，必须
先弄清楚是哪一个点的方向角.
(2023 年梅州市期末)十字测天仪广泛应用于欧洲中世纪晚期的航海领域，主要用于测量太阳等星体的方位，便于船员确定位置，如图 3-8-6(1)所示，十字测天仪由杆 AB 和横档 CD 构成，并且 E 是 CD 的中点，横档与杆垂直并且可在杆上滑动，十字测天仪的使用方法如下：如图 3-8-6(2)，手持十字测天仪，使得眼睛可以从 A 点观察，滑动横档 CD 使得 A，C 在同一水平面上，并且眼睛恰好能观察到太阳，此时视线恰好经过点 D，DE 的影子恰好是AE.然后，通过测量 AE 的长度，可计算出视线和水平面的夹角∠CAD(称为太阳高度角)，最后通过查阅地图来确定船员所在的位置.
图 3-8-6若在一次测量中，AE＝60，横档 CD 的长度为 30，则太阳高
解析：由题意知，AE 垂直平分 CD，
⊙解三角形中的综合问题
(1)解三角形中的综合问题，除灵活运用正、余弦定理及三角形的有关知识外，一般还要用到三角函数，三角恒等变换，平面向量等知识，因此掌握正、余弦定理，三角函数的公式及性质是解题关键.
(2)三角形问题中，涉及变量取值范围或最值问题要注意函数