

2024年河北省邯郸市邯郸冀南新区育华实验学校中考数学三模试卷
展开A.﹣3+1B.﹣3﹣1C.1﹣(﹣3)D.1﹣3
2.(3分)下列运算正确的是( )
A.a2+a2=2a4B.(﹣3a2)3=﹣9a6
C.4a2•a3=4a5D.a6÷a2=a3
3.(3分)在同一平面内到直线的距离等于2的直线有( )
A.1条B.2条C.4条D.无数条
4.(3分)已知a=+1,b=﹣1,则的值为( )
A.B.C.D.3
5.(3分)如图,一个正方体骰子的六个面上分别标有1至6共六个数字,且相对面数字之和相同,将骰子按如图所示方式放置并按箭头方向无滑动翻转后停止在M处,则停止后骰子朝上面的数字为( )
A.3B.4C.5D.6
6.(3分)观察图中尺规作图痕迹,下列结论错误的是( )
A.PQ为∠APB的平分线
B.PA=PB
C.点A、B到PQ的距离不相等
D.∠APQ=∠BPQ
7.(2分)一个小正方体的表面积为3×10﹣2平方米,则每个面的面积用科学记数法表示为( )
A.0.5×10﹣2平方米B.5×10﹣3平方米
C.5×10﹣2平方米D.0.5×10﹣3平方米
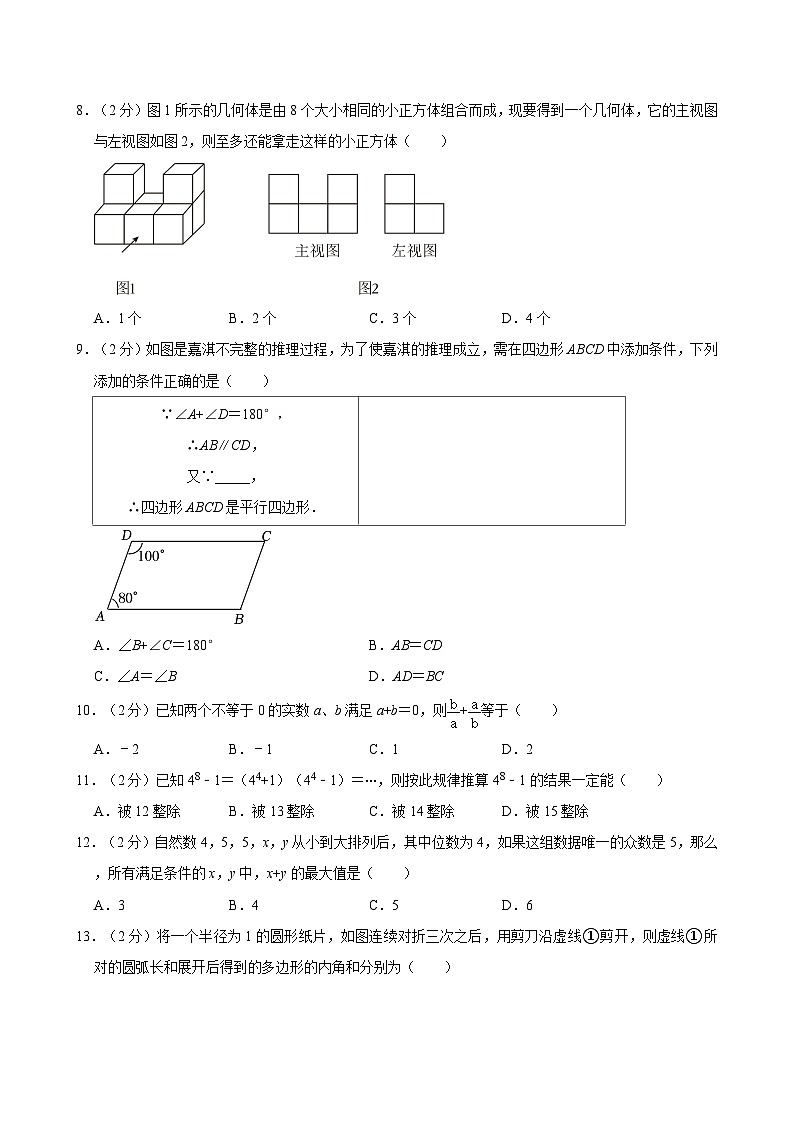
8.(2分)图1所示的几何体是由8个大小相同的小正方体组合而成,现要得到一个几何体,它的主视图与左视图如图2,则至多还能拿走这样的小正方体( )
A.1个B.2个C.3个D.4个
9.(2分)如图是嘉淇不完整的推理过程,为了使嘉淇的推理成立,需在四边形ABCD中添加条件,下列添加的条件正确的是( )
A.∠B+∠C=180°B.AB=CD
C.∠A=∠BD.AD=BC
10.(2分)已知两个不等于0的实数a、b满足a+b=0,则+等于( )
A.﹣2B.﹣1C.1D.2
11.(2分)已知48﹣1=(44+1)(44﹣1)=⋯,则按此规律推算48﹣1的结果一定能( )
A.被12整除B.被13整除C.被14整除D.被15整除
12.(2分)自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么,所有满足条件的x,y中,x+y的最大值是( )
A.3B.4C.5D.6
13.(2分)将一个半径为1的圆形纸片,如图连续对折三次之后,用剪刀沿虚线①剪开,则虚线①所对的圆弧长和展开后得到的多边形的内角和分别为( )
A.B.C.D.
14.(2分)在作业纸上,AB∥EF,点C在AB,EF之间,要得知两相交直线AB,CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2),对于方案I、II,说法正确的是( )
A.I可行,II不可行B.I不可行,II可行
C.I、II都可行D.I、II都不可行
15.(2分)如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置.已知△ABC的面积为16,阴影部分三角形的面积9.若AA′=1,则A′D等于( )
A.2B.3C.4D.
16.(2分)如图,在▱ABCD中,对角线AC,BD相交于点O,AC⊥BC,BC=4,∠ABC=60°.若EF过点O且与边AB,CD分别相交于点E,F,设BE=x,OE2=y,则y关于x的函数图象大致为( )
A.B.
C.D.
二.填空题(17题3分,18题每空2分,19题第一空3分,第二空1分,共11分)
17.(3分)由x<y得到ax>ay,则a的取值范围是 .
18.(4分)如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠1=39°,则∠AOC= .
19.(4分)如图,在▱OABC中,点C(3,0),点A(1,3),反比例函数的图象经过点B,反比例函数的图象与BC交于点F,与折线OAB交于点E.
(1)k= ;
(2)若▱OABC夹在y1,y2之间的整数点(横、纵坐标均为整数的点)有7个(包括边界),则m的取值范围为 .
三.解答题(共71分)
20.(9分)已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
21.(9分)在计算题目:“已知:M=3x2﹣4x+2,N=■,求2M﹣N”时,嘉淇把“2M﹣N”看成“M﹣2N”,得到的计算结果是﹣x2+4x﹣4.
(1)求整式N;
(2)判断2M﹣N的化简结果是否能为负数,并说明理由.
22.(8分)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,则重新转动转盘.
(1)请你用树状图或列表的方法,求M点落在正方形ABCD面上(含内部与边界)的概率;
(2)将正方形ABCD平移整数个单位,则是否存在某种平移,使点M落在正方形ABCD面上的概率为?若存在,指出一种具体的平移过程;若不存在,请说明理由.
23.(9分)在测浮力的实验中,将一长方体石块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F拉力(N)与石块下降的高度x(cm)之间的关系如图所示.
(1)求AB所在直线的函数表达式;
(2)当石块下降的高度为8cm时,求此刻该石块所受浮力的大小.
(温馨提示:当石块位于水面上方时,F拉力=G重力;当石块入水后,F拉力=G重力﹣F浮力.)
24.(11分)某款“不倒翁”的主视图如图1,它由半圆O和等边△PAB组成,直径AB=8cm,半圆O的中点为点C,MN为桌面,半圆O与MN相切于点Q,拨动“不倒翁”后它在桌面MN上做无滑动的滚动.
(1)如图1,AB∥MN,请直接写出PC的长为 cm(结果保留根号);
(2)如图2,当PB⊥MN时,连接OQ,OC.
①直接写出∠COQ的度数.
②求点C到桌面MN的距离(结果保留根号);
(3)当PA或PB垂直于MN时“不倒翁”开始折返,直接写出从PB⊥MN滚动到PA⊥MN(图2﹣图3)过程中,圆心O移动的距离.
25.(12分)已知:如图抛物线y=ax2+3x+c(a≠0)与y轴交于点(0,4),顶点为点D.点A,B的坐标分别为(4,1),(6,4).
(1)①c= ;
②请用含a的式子表示顶点D的坐标.
(2)抛物线y=ax2+3x+c(a≠0)与线段AB有一个公共点时,求a的取值范围;
(3)如图,连接AD,BD,△ABD的面积是否发生变化,若不变请直接写出其面积;若变化,请说明理由.
26.(13分)如图,矩形ABCD中,AB=4,AD=3,点E在折线CB﹣BA上运动(点E不与点C,A重合),DE的中点为G,将EG绕点E顺时针旋转90°得到EF.设点E的运动路径长为x.
(1)如图1,当点E与点B重合时,点F到直线BC的距离为 ;
(2)如图2,当点F落在矩形ABCD的边(或边所在的直线)上时,求x的值;
(3)过点F作FN∥DE,交AD延长线于点N(如图3),设DN的长为y,请直接写出y与x的函数解析式.
2024年河北省邯郸市冀南新区育华实验学校中考数学三模试卷
参考答案与试题解析
一.选择题(共38分,1-6每题3分,7-16每题2分.)
1.(3分)数轴上点A表示﹣3,点B表示1,则表示A、B两点间的距离的算式是( )
A.﹣3+1B.﹣3﹣1C.1﹣(﹣3)D.1﹣3
【解答】解:依题意得:1>﹣3,
∴A、B两点间的距离为:1﹣(﹣3).
故选:C.
2.(3分)下列运算正确的是( )
A.a2+a2=2a4B.(﹣3a2)3=﹣9a6
C.4a2•a3=4a5D.a6÷a2=a3
【解答】解:A.a2+a2=2a2,
则A不符合题意;
B.(﹣3a2)3=﹣27a6,
则B不符合题意;
C.4a2•a3=4a2+3=4a5,
则C符合题意;
D.a6÷a2=a4,
则D不符合题意;
故选:C.
3.(3分)在同一平面内到直线的距离等于2的直线有( )
A.1条B.2条C.4条D.无数条
【解答】解:同一平面内到直线的距离等于2的直线有2条,
故选:B.
4.(3分)已知a=+1,b=﹣1,则的值为( )
A.B.C.D.3
【解答】解:∵a=+1,b=﹣1,
∴ab=(+1)(﹣1)
=2﹣1
=1,
∴==2.
故选:B.
5.(3分)如图,一个正方体骰子的六个面上分别标有1至6共六个数字,且相对面数字之和相同,将骰子按如图所示方式放置并按箭头方向无滑动翻转后停止在M处,则停止后骰子朝上面的数字为( )
A.3B.4C.5D.6
【解答】解:∵一个正方体骰子的六个面上分别标有1至6共六个数字,且相对面数字之和相同,
∴1的对面是6,2的对面是5,3的对面是4,
∴翻转第一次时3朝下,4朝上;翻转第二次时2朝下,5朝上;翻转第三次时4朝下,3朝上;翻转四次时1朝下,6朝上.
故选:D.
6.(3分)观察图中尺规作图痕迹,下列结论错误的是( )
A.PQ为∠APB的平分线
B.PA=PB
C.点A、B到PQ的距离不相等
D.∠APQ=∠BPQ
【解答】解:∵由图可知,PQ是∠APB的平分线,
∴A,B,D正确;
∵PQ是∠APB的平分线,PA=PB,
∴点A、B到PQ的距离相等,故C错误.
故选:C.
7.(2分)一个小正方体的表面积为3×10﹣2平方米,则每个面的面积用科学记数法表示为( )
A.0.5×10﹣2平方米B.5×10﹣3平方米
C.5×10﹣2平方米D.0.5×10﹣3平方米
【解答】解:∵小正方体有6个面,且每个面都是正方形,
∴(3×10﹣2)÷6=0.5×10﹣2=5×10﹣3(平方米),
故选:B.
8.(2分)图1所示的几何体是由8个大小相同的小正方体组合而成,现要得到一个几何体,它的主视图与左视图如图2,则至多还能拿走这样的小正方体( )
A.1个B.2个C.3个D.4个
【解答】解:由题意可知,该几何体的底层至少需要3个小正方体,上层至少需要2个小正方体,
所以至多还能拿走这样的小正方体3个.
故选:C.
9.(2分)如图是嘉淇不完整的推理过程,为了使嘉淇的推理成立,需在四边形ABCD中添加条件,下列添加的条件正确的是( )
A.∠B+∠C=180°B.AB=CD
C.∠A=∠BD.AD=BC
【解答】解:∵∠A+∠D=180°,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形.
故选:B.
10.(2分)已知两个不等于0的实数a、b满足a+b=0,则+等于( )
A.﹣2B.﹣1C.1D.2
【解答】解:方法一:+
=
=
=,
∵两个不等于0的实数a、b满足a+b=0,
∴ab≠0,
当a+b=0时,原式==﹣2,
故选:A.
方法二:∵两个不等于0的实数a、b满足a+b=0,
∴a=﹣b,
∴+
=
=﹣1+(﹣1)
=﹣2,
故选:A.
11.(2分)已知48﹣1=(44+1)(44﹣1)=⋯,则按此规律推算48﹣1的结果一定能( )
A.被12整除B.被13整除C.被14整除D.被15整除
【解答】解:48﹣1
=(44+1)(44﹣1)
=(44+1)(42+1)(42﹣1)
=(44+1)(42+1)×15.
故选:D.
12.(2分)自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么,所有满足条件的x,y中,x+y的最大值是( )
A.3B.4C.5D.6
【解答】解:唯一的众数是5,中位数为4,故x,y不相等且x<4,y<4.
x、y的取值为0,1,2,3,则x+y的最大值为2+3=5.
故选:C.
13.(2分)将一个半径为1的圆形纸片,如图连续对折三次之后,用剪刀沿虚线①剪开,则虚线①所对的圆弧长和展开后得到的多边形的内角和分别为( )
A.B.C.D.
【解答】解:根据题意得虚线①所对的圆弧对的圆心角为45°,展开后得到的多边形为正八边形,
所以虚线①所对的圆弧长为=,
展开后得到的多边形的内角和为180°×(8﹣2)=1080°.
故选:C.
14.(2分)在作业纸上,AB∥EF,点C在AB,EF之间,要得知两相交直线AB,CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2),对于方案I、II,说法正确的是( )
A.I可行,II不可行B.I不可行,II可行
C.I、II都可行D.I、II都不可行
【解答】解:如图1,延长CD交AB于Q,过C作CM∥AB,而AB∥EF,
∴AB∥CM∥EF,
∴∠AQC=∠QCM,∠E=∠MCE,
∴∠AQC=∠QCM=∠DCE﹣∠MCE=∠DCE﹣∠E,
∴I方案可行,
如图2,延长CD交AB于Q,
∵AB∥EF,
∴∠AQC=∠CME,
∴II方案可行,
故选:C.
15.(2分)如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置.已知△ABC的面积为16,阴影部分三角形的面积9.若AA′=1,则A′D等于( )
A.2B.3C.4D.
【解答】解:设A′B′交BC于E,A′C′交BC于F.
∵S△ABC=16、S△A′EF=9,且AD为BC边的中线,
∴S△A′DE=S△A′EF=,S△ABD=S△ABC=8,
∵将△ABC沿BC边上的中线AD平移得到△A'B'C',
∴A′E∥AB,
∴△DA′E∽△DAB,
则()2=,即()2=,
解得A′D=3或A′D=﹣(舍),
故选:B.
16.(2分)如图,在▱ABCD中,对角线AC,BD相交于点O,AC⊥BC,BC=4,∠ABC=60°.若EF过点O且与边AB,CD分别相交于点E,F,设BE=x,OE2=y,则y关于x的函数图象大致为( )
A.B.
C.D.
【解答】解:过O点作OM⊥AB于M,
∵AC⊥BC,∠ABC=60°,
∴∠BAC=30°,
∵BC=4,
∴AB=8,AC=,
∵四边形ABCD为平行四边形,
∴AO=AC=,
∴OM=AO=,
∴AM=,
设BE=x,OE2=y,则EM=AB﹣AM﹣BE=8﹣3﹣x=5﹣x,
∵OE2=OM2+EM2,
∴y=(x﹣5)2+3,
∴抛物线开口方向向上,顶点坐标为(5,3),与y轴的交点为(0,28),
∵0≤x≤8,
∴当x=8时y=12,
故符合解析式的图象为:
故选:C.
二.填空题(17题3分,18题每空2分,19题第一空3分,第二空1分,共11分)
17.(3分)由x<y得到ax>ay,则a的取值范围是 .
【解答】解:∵x<y,ax>ay,
∴a<0.
故答案为:a<0.
18.(4分)如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠1=39°,则∠AOC= .
【解答】解:解法一:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,
∴∠ABC=∠1=39°,
∵OA=OB=OC,
∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×39°=78°;
解法二:
连接OB,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,
∴∠AOD=∠BOD,∠BOE=∠COE,
∵∠DOE+∠1=180°,∠1=39°,
∴∠DOE=141°,即∠BOD+∠BOE=141°,
∴∠AOD+∠COE=141°,
∴∠AOC=360°﹣(∠BOD+∠BOE)﹣(∠AOD+∠COE)=78°;
故答案为:78°.
19.(4分)如图,在▱OABC中,点C(3,0),点A(1,3),反比例函数的图象经过点B,反比例函数的图象与BC交于点F,与折线OAB交于点E.
(1)k= ;
(2)若▱OABC夹在y1,y2之间的整数点(横、纵坐标均为整数的点)有7个(包括边界),则m的取值范围为 .
【解答】解:(1)∵OC=3,点A(1,3),
∴将点A向右平移3个单位长度得到点B(4,3),
将点B(4,3)代入中,得k=12;
(2)▱OABC中的整数点如图所示:
将点A(1,3)代入,得m=3;将点(1,2)代入,得m=2;
∴若▱OABC夹在y1,y2之间的整数点有7个(包括边界),则m的取值范围为2<m≤3,
故答案为:(1)12;(2)2<m≤3.
三.解答题(共71分)
20.(9分)已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
【解答】解:(1)∵360°÷180°=2,
630°÷180°=3……90°,
∴甲的说法对,乙的说法不对,
360°÷180°+2
=2+2
=4.
答:甲同学说的边数n是4;
(2)依题意有(n+x﹣2)×180°﹣(n﹣2)×180°=540°,
解得x=3.
故x的值是3.
21.(9分)在计算题目:“已知:M=3x2﹣4x+2,N=■,求2M﹣N”时,嘉淇把“2M﹣N”看成“M﹣2N”,得到的计算结果是﹣x2+4x﹣4.
(1)求整式N;
(2)判断2M﹣N的化简结果是否能为负数,并说明理由.
【解答】解:(1)根据题意得:N=[3x2﹣4x+2﹣(﹣x2+4x﹣4)]=2x2﹣4x+3;
(2)2M﹣N=2(3x2﹣4x+2)﹣(2x2﹣4x+3)=6x2﹣8x+4﹣2x2+4x﹣3=4x2﹣4x+1=(2x﹣1)2,
∵(2x﹣1)2≥0.
∴2M﹣N的化简结果不能为负数.
22.(8分)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,则重新转动转盘.
(1)请你用树状图或列表的方法,求M点落在正方形ABCD面上(含内部与边界)的概率;
(2)将正方形ABCD平移整数个单位,则是否存在某种平移,使点M落在正方形ABCD面上的概率为?若存在,指出一种具体的平移过程;若不存在,请说明理由.
【解答】解:(1)正方形四个顶点的坐标分别是A(﹣2,2);B(﹣2,﹣2);C(2,﹣2);D(2,2),
列表得:
M点的坐标所有的情况有共16种,
其中落在正方形ABCD面上(含内部与边界)的有(1,1),(1,2),(2,1),(2,2),共4种,所以M点落在正方形ABCD面上(含内部与边界)的概率是=;
(2)若使点M落在正方形ABCD面上的概率为,则只有4个点不在正方形内部,所以可把正方形ABCD向右平移2个单位长度,再向上平移1个单位长度或者向右平移1个单位长度,向上平移2个单位长度即可.
23.(9分)在测浮力的实验中,将一长方体石块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F拉力(N)与石块下降的高度x(cm)之间的关系如图所示.
(1)求AB所在直线的函数表达式;
(2)当石块下降的高度为8cm时,求此刻该石块所受浮力的大小.
(温馨提示:当石块位于水面上方时,F拉力=G重力;当石块入水后,F拉力=G重力﹣F浮力.)
【解答】解:(1)设AB所在直线的函数表达式为F拉力=kx+b,将(6,4),(10,2.5)代入得:
,
解得,
∴AB所在直线的函数表达式为F拉力=﹣x+;
(2)在F拉力=﹣x+中,令x=8得F拉力=﹣×8+=,
∵4﹣=(N),
∴当石块下降的高度为8cm时,该石块所受浮力为N.
24.(11分)某款“不倒翁”的主视图如图1,它由半圆O和等边△PAB组成,直径AB=8cm,半圆O的中点为点C,MN为桌面,半圆O与MN相切于点Q,拨动“不倒翁”后它在桌面MN上做无滑动的滚动.
(1)如图1,AB∥MN,请直接写出PC的长为 cm(结果保留根号);
(2)如图2,当PB⊥MN时,连接OQ,OC.
①直接写出∠COQ的度数.
②求点C到桌面MN的距离(结果保留根号);
(3)当PA或PB垂直于MN时“不倒翁”开始折返,直接写出从PB⊥MN滚动到PA⊥MN(图2﹣图3)过程中,圆心O移动的距离.
【解答】解:(1)由题意得:当AB∥MN时,P,O,C三点在一条直线上,
∵直径AB=8cm,
∴OC=AB=4cm,
∵△PAB为等边三角形,
∴PA=AB=PB=8cm,∠PAB=60°,
∵OA=OB,
∴PO⊥AB,
∴PO=PA•sin60°=8×=4(cm),
∴PC=PO+OC=(4+4)cm.
故答案为:4+4;
(2)①∠COQ的度数=30°.
∵半圆O与MN相切于点Q,
∴OQ⊥MN,
∵PB⊥MN,
∴PB∥OQ,
∴∠QOB=∠PBA=90°,
∵半圆O的中点为点C,
∴∠BOC=90°,
∴∠COQ=∠BOC﹣∠BOQ=30°.
②过点C作CH⊥MN于点H,CK⊥OQ于点K,如图,
∵∠COQ=30°,CK⊥OQ,
∴CK=OC=2cm,
∴OK==2(cm),
∴QK=OQ﹣OK=(4﹣2)cm,
∵CH⊥MN,CK⊥OQ,OQ⊥MN,
∴四边形CHQK为矩形,
∴CH=QK=(4﹣2)cm.
∴点C到桌面MN的距离为(4﹣2)cm.
(3)从PB⊥MN滚动到PA⊥MN(图2﹣图3)过程中,圆心O移动的距离为cm.
∵拨动“不倒翁”后它在桌面MN上做无滑动的滚动,
∴滚动过程中始终与桌面MN相切,
∴圆心O到桌面的距离总等于圆的半径,
∴从PB⊥MN滚动到PA⊥MN过程中,圆心O移动的距离为的长度的2倍,
由(2)①知:∠COQ=30°,
∴圆心O移动的距离==(cm).
25.(12分)已知:如图抛物线y=ax2+3x+c(a≠0)与y轴交于点(0,4),顶点为点D.点A,B的坐标分别为(4,1),(6,4).
(1)①c= ;
②请用含a的式子表示顶点D的坐标.
(2)抛物线y=ax2+3x+c(a≠0)与线段AB有一个公共点时,求a的取值范围;
(3)如图,连接AD,BD,△ABD的面积是否发生变化,若不变请直接写出其面积;若变化,请说明理由.
【解答】解:(1)①∵抛物线y=ax2+3x+c(a≠0)与y轴交于点(0,4),
∴c=4,
故答案为:4;
②抛物线解析式为y=ax2+3x+4,
根据顶点坐标公式:x=﹣,
y=a(﹣)2+3(﹣)+4==﹣,
∴D(﹣,﹣+4);
(2)设线段AB的解析式为y=kx+b,将A(4,1)、B(6,4)代入得:
,解得,
∴直线AB的解析式为y=,
当抛物线经过点A时,如图,此时有:1=a×42+3×4+4,
解得:a=﹣,
当抛物线经过点B时,如图,此时有:4=a×62+3×6+4,
解得:a=﹣,
当抛物线的顶点在直线AB上时,
,
此方程无解,
∴a的取值范围为:;
(3)不变,理由如下:
分别过点A,B,D作AE⊥x轴,BF⊥x轴,DG⊥x轴,
∴S△ABD=S梯形BFGD﹣S梯形BFEA﹣S梯形AEGD
=(4+4﹣)(6+)﹣×(4+1)×(6﹣4)﹣(1+4﹣)(4+)
=24﹣﹣﹣10++﹣5
=9.
26.(13分)如图,矩形ABCD中,AB=4,AD=3,点E在折线CB﹣BA上运动(点E不与点C,A重合),DE的中点为G,将EG绕点E顺时针旋转90°得到EF.设点E的运动路径长为x.
(1)如图1,当点E与点B重合时,点F到直线BC的距离为 ;
(2)如图2,当点F落在矩形ABCD的边(或边所在的直线)上时,求x的值;
(3)过点F作FN∥DE,交AD延长线于点N(如图3),设DN的长为y,请直接写出y与x的函数解析式.
【解答】解:(1)如图1,
作FH⊥BC于H,
∴∠FHE=90°,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
∴∠FHE=∠A,
∵EG绕点E顺时针旋转90°得到EF,
∴EF=EG,∠DEF=90°,
∴∠GEF=∠ABC,
∴∠ABD=∠FEH,
∴△ABD∽△HEF,
∴,
∵G是DE的中点,
∴DE=2EG=2EF,
∴,
∴FH==,
故答案为:;
(2)如图2,
当点E在BC上,点F在CD所在的直线是上时,
∵∠DEF=90°,
∴∠FEC+∠DEC=90°,
∵四边形ABCD是矩形,
∴∠ECF=∠DCE=90°,CD=AB=4,
∴∠DEC+∠CDE=90°,
∴∠CDE=∠FEC,
∴△ECF∽△DEC,
∴,
∴CE=,
∴x=2,
如图3,
当点E在AB上,当F在BC上时,
同理上可得,
△EBF∽△DAE,
∴,
∴BE=AD=,
∴x=BC+BE=2+,
综上所述:x=2或;
(3)如图3,
当点E在BC上时,作DH⊥FN于H,作EQ⊥AD于Q,
∴∠DHN=∠DHF=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴四边形ABEQ是矩形,
∴EQ=AB=4,
∵∠DEF=90°,FN∥DE,
∴∠F=180°﹣∠DEF=90°,
∴四边形DEFH是矩形,
∴DH=EF,∠HDE=90°,DH=EF,
∴∠HDN+∠EDQ=90°,
∵∠DHN=∠EQD=90°,
∴∠QED+∠EDQ=90°,
∴∠QED=∠HDN,
∴△DHN∽△EQD,
∴,
∴DN=,
∵DH=EF=ED,
∴y==ED2,
∵ED2=DQ2+EQ2=CE2+EQ2=x2+16,
∴y=(0<x≤3),
如图4,
当点E在AB上时,
同理可得,
△DHN∽△EAD,
∴,
∴DE=,
∵AE=7﹣x,ED2=AE2+AD2=(7﹣x)2+9,
∴y=(3<x<7),
综上所述:y=.∵∠A+∠D=180°,
∴AB∥CD,
又∵_____,
∴四边形ABCD是平行四边形.
∵∠A+∠D=180°,
∴AB∥CD,
又∵_____,
∴四边形ABCD是平行四边形.
a
b
1
2
3
4
1
(1,1)
(2,1)
(3,1)
(4,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
河北省邯郸冀南新区育华实验学校2023-2024学年八年级上学期期中数学试题: 这是一份河北省邯郸冀南新区育华实验学校2023-2024学年八年级上学期期中数学试题,共10页。试卷主要包含了若点与点关于x轴对称,则,在五边形ABCDE中,,,,则,如图3,在中,,,则为,根据下列条件,不能画出唯一的是等内容,欢迎下载使用。
河北省邯郸冀南新区育华实验学校2023-2024学年七年级上学期期中数学试题: 这是一份河北省邯郸冀南新区育华实验学校2023-2024学年七年级上学期期中数学试题,共7页。试卷主要包含了5D,下列各组中的两项属于同类项的是,下列各组中的运算结果相等的是,下列各式变形后与不同的是,若,则等内容,欢迎下载使用。
河北省邯郸冀南新区育华实验学校2023—2024学年上学期七年级数学期中考试: 这是一份河北省邯郸冀南新区育华实验学校2023—2024学年上学期七年级数学期中考试,共10页。试卷主要包含了+202318等内容,欢迎下载使用。












