





中职高教版(2021·十四五)9.2 正态分布优质课件ppt
展开在日常生活和生产实践中,经常还会遇到这样一类随机变量,它们受众多的、互不相干的、不分主次的偶然因素共同作用,其概率分布往往服从或近似服从正态分布.
如图所示为高尔顿钉板实验的示意图,每一圆点表示钉在木板上的一颗钉子,所有相邻钉子之间的距离均相等.在入 口处放入一个直径小于两颗钉子之问距离的小圆球,在小圆球向下降落的过程中,碰到钉子后皆以0.5的概率向左或向右滚下,直到最后落入木板下方的空槽内.试作小球落入空槽内的频率分布直方图.
把空槽从左向右分成区间段,根据实验数据可得如图所示的频率分布直方图.
如果把上述小球落入的区间从左往右编号1,2,…,10,那么区间的编号ξ可以看做离散型随机变量.
若将相邻钉子之间的距离逐渐缩小,则上述频率分布直方图中的折线就会逐渐接近下图中的钟形曲线,称为正态曲线.相应于上述正态曲线,其随机变量ξ的取值范围是一个区间,称这样的随机变量为连续型随机变量.
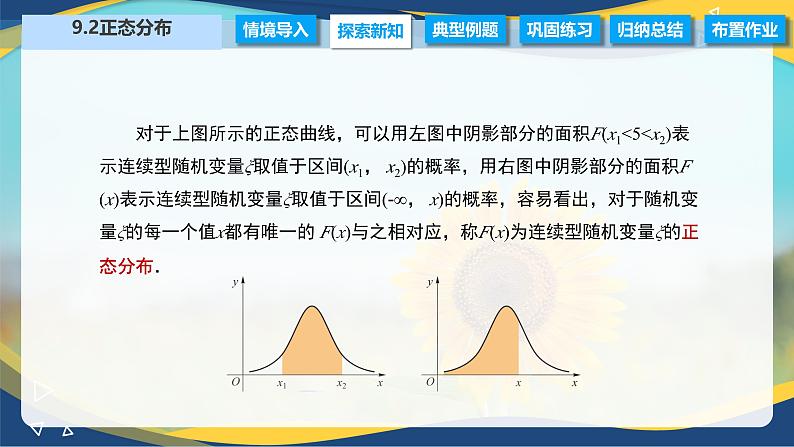
对于上图所示的正态曲线,可以用左图中阴影部分的面积F(x1<5
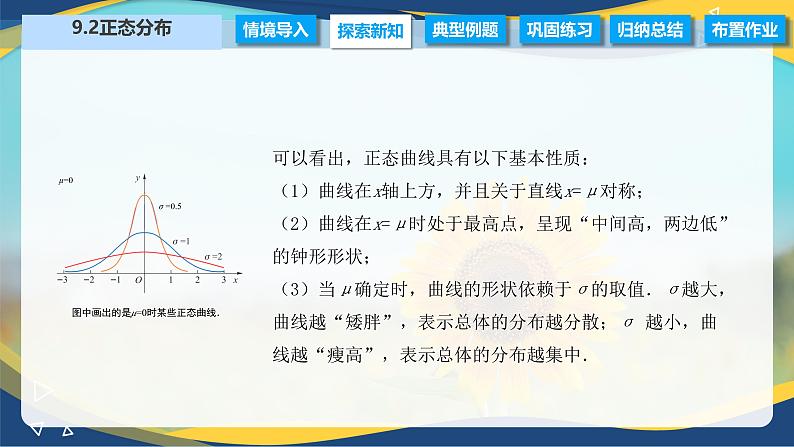
图中画出的是μ=0时某些正态曲线.
可以看出,正态曲线具有以下基本性质:(1)曲线在x轴上方,并且关于直线x=μ对称; (2)曲线在x=μ时处于最高点,呈现“中间高,两边低”的钟形形状;(3)当μ确定时,曲线的形状依赖于σ的取值.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ 越小,曲线越“瘦高”,表示总体的分布越集中.
参数μ=0, σ =1 的正态分布称为标准正态分布,记作N(0,1). 当随机变量ξ服从标准正态分布时,将ξ的取值小于x的概率记作Φ(x),即Φ(x)=P(ξ
例1 若ξ ~N(0,1),查表计算: (1)P(ξ <2.8) ; (2)P(ξ ≥2); (3)P(ξ <-1).
例2 若ξ ~N(1,2²),查表计算: (1) P(ξ <3) ; (2) P(ξ ≥-2).
研究表明,服从正态分布N(μ,σ²)的随机变量ξ在区间(μ-σ, μ+σ),(μ-2σ, μ+2σ),(μ-3σ, μ+3σ)内取值的概率分别是0.6826,0.9544,0.9974,如图所示.
可以看出,服从正态分布的随机变量ξ几乎总是取之于区间(μ-3σ, μ+3σ)之内,而在此区间以外取值的概率只有0.0026,也就是说ξ在此区间以外取值是小概率事件,这种情况在一次试验中是几乎不可能发生的,在实际应用中,通常认为服从正态分布N(μ,σ²)的随机变量ξ只取区间(μ-3σ, μ+3σ)内的值,这就是正态分布的3σ原则.
例3 在某次数学考试中,考生的成绩ξ服从正态分布 N(120, 100). (1)求考生成绩ξ位于区间(110, 130)内的概率;(2)若此次考试共有2000名考生,试估计成绩在区间(100,140)内的考生人数.
1.设ξ ~N(1,9),求P(ξ≥10)和P(ξ <4) .2. 某校高三男生共1000人.他们的身高X (单位:cm)近似服从正态分布 N(176,16), 身高在区间(172,180)内的男生人数大约有多少? 3. 某批灯有10000 个,其寿命(单位:h)服从正态分布N(1000,100²),试估计寿命在下列范围内的灯的个数. (1)(900,1100) ; (2)(800,1200) .
作 业
1.书面作业:完成教材第149页习题9.2;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.
高教版(2021·十四五)拓展模块一(上册)4.2.1 共面直线精品课件ppt: 这是一份高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053649_t3/?tag_id=26" target="_blank">4.2.1 共面直线精品课件ppt</a>,共17页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,21共面直线,情境导入,异面直线,平行直线,相交直线等内容,欢迎下载使用。
中职数学高教版(2021·十四五)拓展模块一(上册)2.3 向量的内积优秀ppt课件: 这是一份中职数学高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053622_t3/?tag_id=26" target="_blank">2.3 向量的内积优秀ppt课件</a>,共15页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,3向量的内积,情境导入,向量的夹角,练一练,向量的内积等内容,欢迎下载使用。
中职数学高教版(2021·十四五)拓展模块一(上册)第2章 平面向量2.1 向量的概念一等奖课件ppt: 这是一份中职数学高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053616_t3/?tag_id=26" target="_blank">第2章 平面向量2.1 向量的概念一等奖课件ppt</a>,共17页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,1向量的概念,情境导入,向量的概念,向量的表示,向量的模等内容,欢迎下载使用。












