

2023-2024学年广西贺州市七年级(下)期末数学试卷(含详细答案解析)
展开1.−1的立方根是( )
A. −1B. 1C. ±1D. 没有立方根
2.下列分式中,是最简分式的是( )
A. aabB. 2y2xC. x−1xD. 1−aa−1
3.下列整式与ab3为同类项的是( )
A. a2bB. −2ab3C. abD. ab2c
4.若x>y,下列不等式不成立的是( )
A. x−5>y−5B. 3x>3y
C. −2x+5>−2y+5D. m2x≥m2y
5.判断下列各式,计算正确的是( )
A. a2⋅a3=a6B. (b2)3=b5C. 3x2−4x2=x2D. (−2ab)2=4a2b2
6.在化学课上,化学老师提到:“物品A的保存温度要求为“大于1℃”,物品B的保存温度要求为“不大于2℃”,若需要将A,B两种物品放在一起保存,则药品保存温度要求在数轴上表示为( )
A. B.
C. D.
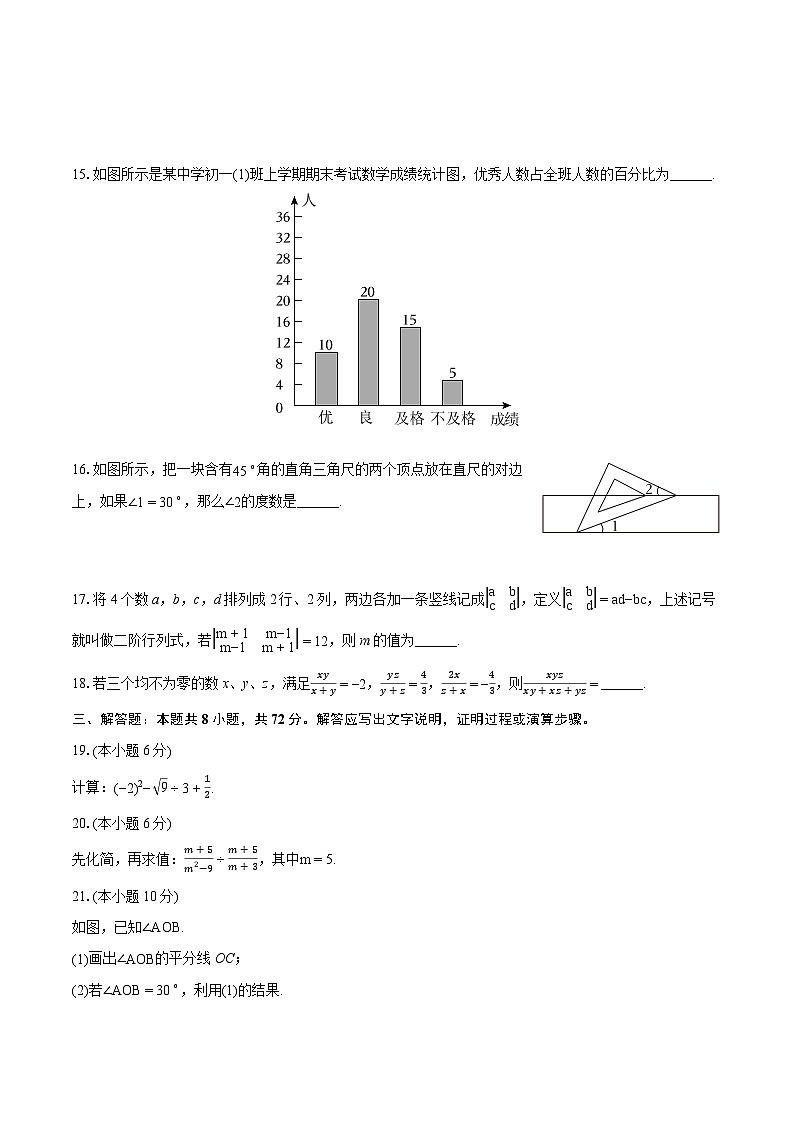
7.方程组3x+2y=7,6x−2y=11的解是( )
A. x=−1,y=5B. x=1,y=2C. x=3,y=−1D. x=2,y=12
8.如图所示,运行程序从“输入整数x”到“结果是否大于21”为一次程序操作,若输入整数x后程序操作仅进行了2次就停止,则x的值是( )
A. 5B. 6C. 10D. 11
9.如图,直线AB//CD,∠C=44∘,∠E为直角,则∠1等于( )
A. 138∘
B. 136∘
C. 134∘
D. 132∘
10.小红是一名密码翻译爱好者,在她的密码手册中有这样一条信息:a−b,x−3,x+3,a+b,x2−9,a2−b2分别对应下列六个字:州,爱,我,贺,游,美,现将(x2−9)a2−(x2−9)b2因式分解,结果呈现的密码信息可能是( )
A. 我爱贺州B. 美我贺州C. 贺州游D. 我爱美
11.在一次数学活动课中,小林用如图所示的1张小正方形纸片A,4张大正方形纸片B和若干张长方形纸片C恰好拼成一个新的正方形(将纸片进行无空隙,无重叠拼接),则小林共用长方形纸片C为( )
A. 2张B. 4张C. 6张D. 8张
12.如图,a//b,直线a,b被直线c所截,AC1、BC1分别平分∠EAB、∠FBA交于点C1,得∠C1=90∘;AC2、BC2分别平分∠EAC1,∠FBC1交于点C2,得∠C2=45∘;AC3、BC3分别平分∠EAC2、∠FBC2交于点C3,得∠C3=22.5∘,…,依此规律,则∠C2024的度数为( )
A. (9022025)∘B. (9022024)∘C. (9022023)∘D. (9022022)∘
二、填空题:本题共6小题,每小题2分,共12分。
13. 4=______.
14.如图天平左盘放3个乒乓球,右盘放5g砝码,天平倾斜,设每个乒乓球的质量为x(g),请写出x与5之间的关系:______.(用不等式表示)
15.如图所示是某中学初一(1)班上学期期末考试数学成绩统计图,优秀人数占全班人数的百分比为______.
16.如图所示,把一块含有45∘角的直角三角尺的两个顶点放在直尺的对边上,如果∠1=30∘,那么∠2的度数是______.
17.将4个数a,b,c,d排列成2行、2列,两边各加一条竖线记成abcd,定义abcd=ad−bc,上述记号就叫做二阶行列式,若m+1m−1m−1m+1=12,则m的值为______.
18.若三个均不为零的数x、y、z,满足xyx+y=−2,yzy+z=43,2xz+x=−43,则xyzxy+xz+yz=______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题6分)
计算:(−2)2− 9÷3+12.
20.(本小题6分)
先化简,再求值:m+5m2−9÷m+5m+3,其中m=5.
21.(本小题10分)
如图,已知∠AOB.
(1)画出∠AOB的平分线OC;
(2)若∠AOB=30∘,利用(1)的结果.
①求∠BOC的度数;
②试求∠AOC的补角.
22.(本小题10分)
定义一种幂的新运算:xa⊕xb=xab+xa+b.如:3⊕32=31×2+31+2=32+33=9+27=36,请利用这种运算规则解决下列问题:
(1)求22⊕23的值;
(2)2p=3,2q=5,3q=6,求2p⊕2q的值.
23.(本小题10分)
如图,是某学校内的一块长为30米,宽为15米的长方形劳动实践基地,为了行走方便,学校决定请工人对三条都一样宽的走道进行硬化(阴影部分).设走道的宽为x米.
(1)求走道的全面积为______;(试用含x的代数式表示并化简)
(2)经测量该走道的宽x为0.5米,求出该走道的总面积;
(3)经商议按25元/米 2的费用支付给工人工钱,则学校要付给工人的费用是多少元?
24.(本小题10分)
阅读以下材料,并按要求完成相应任务:
在因式分解中、多项式中某一部分重复出现时,把这些重复的部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种解题方法称为“换元法”.
下面是小明同学用换元法对多项式(x2+4x+1)(x2+4x+7)+9进行因式分解的过程.
解:设x2+4x=y,则
原式=(y+1)(y+7)+9(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2+4x+4)2(第四步)
请根据上述材料回答下列问题:
(1)小明同学的解法中,第二步到第三步运用了因式分解的______;
A.提取公因式法
B.平方差公式法
C.完全平方公式法
(2)老师说,小明同学因式分解的结果不彻底,请你写出该因式分解的最后结果______;
(3)请你用换元法对多项式(x2−6x+8)(x2−6x+10)+1进行因式分解.
25.(本小题10分)
端午节期间,某商店老板用600元购进一批蛋黄粽,又用600元购进了一批肉粽,所购进的肉粽数量是蛋黄粽数量的75%,且每个肉粽的进价比每个蛋黄标的进价多0.5元.
(1)求每个肉粽的进价和每个蛋黄粽的进价分别是多少元;
(2)端午节当天,老板分别以每个5元、每个4元的价格销售肉粽和蛋黄粽,当肉粽售出40%,蛋黄粽售出50%后,为了尽快售完,老板决定将肉粽的单价下降a%,蛋黄粽的单价下降2a%,刚好卖完时,老板的总利润比原计划少195元,求a的值.
26.(本小题10分)
近年来,研学旅行成为素质教育的新内容和新方式,它继承和发展了我国传统游学、“读万卷书,行万里路”的教育理念和人文精神,提升中小学生的自理能力、创新精神和实践能力.2024年6月18日,某中学组织七年级同学到国家5A景区黄姚古镇附近的中小学研学实践基地进行研学.请你认真阅读以下材料,并完成相关的学习任务:
请同学们根据材料一、材料二提供的信息完成2个任务.
任务
(1):求本次研学初一年级共有多少人参加?
任务
(2):学校可以选择几种租车方案?最少租车费用是多少?
答案和解析
1.【答案】A
【解析】解:−1的立方根是−1,
故选:A.
利用立方根定义求出所求即可.
此题考查了立方根,熟练掌握立方根定义是解本题的关键.
2.【答案】C
【解析】解:A、aab=1b,故不是最简分式,不符合题意;
B、2y2x=yx,故不是最简分式,不符合题意;
C、x−1x,是最简分式,符合题意;
D、1−aa−1=−a−1a−1=−1,故不是最简分式,不符合题意;
故选:C.
根据最简分式的定义:一个分式的分子与分母没有公因式时,叫最简分式即可判断.
本题考查了最简分式,解决本题的关键是掌握最简分式的定义.
3.【答案】B
【解析】解:与ab3为同类项的是−2ab3;
故选:B.
根据字母相同,字母的指数也相同的几个单项式,叫作同类项,进行判断即可.
本题考查了同类项,熟练掌握同类项的定义是解题的关键.
4.【答案】C
【解析】解:A、x−5>y−5,成立,不符合题意;
B、3x>3y,成立,不符合题意;
C、−2x+5<−2y+5,原不等式不成立,符合题意;
D、m2x≥m2y,成立,不符合题意.
故选:C.
根据不等式的性质,逐一进行判断即可.
本题考查不等式的性质,掌握不等式的性质是关键.
5.【答案】D
【解析】解:A、a2⋅a3=a5,原计算错误,不符合题意;
B、(b2)3=b6,原计算错误,不符合题意;
C、3x2−4x2=−x2,原计算错误,不符合题意;
D、(−2ab)2=4a2b2,计算正确,符合题意.
故选:D.
根据同底数幂的乘法,幂的乘方与积的乘方,合并同类项的法则,逐一进行计算判断即可.
本题考查了同底数幂的乘法,幂的乘方与积的乘方,合并同类项,掌握同底数幂的乘法,幂的乘方与积的乘方,合并同类项的法则是关键.
6.【答案】C
【解析】解:由题意,得:1<保存温度≤2,在数轴上表示如图:
故选:C.
定方向,定边界,在数轴上表示出不等式的解集即可.
本题考查用数轴表示不等式的解集,解题的关键是掌握相关知识的灵活运用.
7.【答案】D
【解析】【分析】
本题考查了二元一次方程组的解法,熟练掌握二元一次方程组的基本解法是解答本题的关键.
运用加减消元解答即可.
【解答】
解:{3x+2y=7①6x−2y=11②,
①+②得,9x=18,
则x=2,
把x=2代入①得,6+2y=7,解得y=12,
故原方程组的解为:x=2y=12.
故选:D.
8.【答案】B
【解析】解:由题意,得:3x−6≤213(3x−6)−6>21,
解得:5
故选:B.
根据流程图列出不等式组进行求解即可.
本题考查一元一次不等式组的应用,关键是根据流程图列出不等式组.
9.【答案】C
【解析】解:如图,过点E作EF//AB//CD,
∴∠1=∠AEF,∠C+∠FEC=180∘,
∴∠FEC=180∘−44∘=136∘,
∴∠AEF=360∘−90∘−136∘=134∘,
∴∠1=134∘.
故选:C.
过点E作AB的平行线,将角度进行转换,利用圆周角为360∘求出∠1的度数即可.
本题考查平行线的性质,能够灵活运用平行线的性质是解答本题的关键.
10.【答案】A
【解析】解:(x2−9)a2−(x2−9)b2
=(x2−9)(a2−b2)
=(x+3)(x−3)(a+b)(a−b),
∴结果呈现的密码信息可能是:我爱贺州,
故选:A.
将原式因式分解得出结论即可.
本题主要考查因式分解的应用,正确进行因式分解是解题关键.
11.【答案】B
【解析】解:设共用长方形纸片C为m张,则:拼成的大正方形的面积为a2+mab+4b2,
∴a2+mab+4b2为完全平方式,
∴m=4或m=−4(舍去);
∴共用长方形纸片C为4张;
故选:B.
根据题意,得到三种图形的面积之和为一个完全平方式,进行求解即可.
本题考查完全平方公式与几何图形,熟练掌握完全平方公式是关键.
12.【答案】C
【解析】解:由题意,∠C1=90∘=90∘20,∠C2=45∘=90∘21,∠C3=22.5∘=90∘22⋯,
∴Cn=90∘2n−1,
∴∠C2024=(9022023)∘;
故选:C.
根据已知角度,得到Cn=90∘2n−1,进而求出∠C2024即可.
本题考查图形类规律探究,根据题意找出变化规律是解题的关键.
13.【答案】2
【解析】解:∵22=4,
∴4的算术平方根是2,即 4=2.
故答案为:2.
利用算术平方根定义计算即可求出值.
此题考查了算术平方根,熟练掌握算术平方根的定义是解本题的关键.
14.【答案】3x>5
【解析】解:由题意知3x>5,
故答案为:3x>5.
根据天平倾斜方向知左侧托盘质量大于右边,据此可得答案.
本题主要考查由实际问题抽象出一元一次不等式,用不等式表示不等关系时,要抓住题目中的关键词,如“大于(小于)、不超过(不低于)、是正数(负数)”、“至少”、“最多”等等,正确选择不等号.
15.【答案】20%
【解析】解:1010+20+15+5×100%=20%;
故答案为:20%.
利用优秀的人数除以总人数,进行求解即可.
本题考查了条形统计图的运用.读懂统计图,从统计图上得到必要的信息是解题的关键.
16.【答案】15∘
【解析】解:如图所示:由题意得,AB//CD,
∴∠1=∠3=30∘,
∵三角板为含有45∘角的直角三角板,
∴∠2=45∘−∠3=45∘−30∘=15∘,
故答案为:15∘.
根据题意可得AB//CD,根据平行线的性质可得∠1=∠3,然后根据已知三角板含有45∘角的直角三角板,可得∠2=45∘−∠3,即可求解.
本题考查了平行线的性质,解答本题的关键是掌握平行线的性质:两直线平行,内错角相等.
17.【答案】3
【解析】解:由题意,得:(m+1)2−(m−1)2=12,
∴m2+2m+1−m2+2m−1=12,
∴4m=12,
∴m=3;
故答案为:3.
根据新运算,列出方程,进行求解即可.
本题考查定义新运算,完全平方公式,解一元一次方程,弄清题中的新定义是解本题的关键.
18.【答案】−4
【解析】解:∵xyx+y=−2,yzy+z=43,zxz+x=−43,
∴1x+1y=−12,1y+1z=34,1z+1x=−34,
∴1x+1y+1z=−14,
则xyzxy+yz+zx=11x+1y+1z=−4.
故答案为:−4
所求式子分子分母除以xyz变形后,将已知三等式左边变形后代入计算即可求出值.
此题考查了分式的化简求值,将已知等式及所求式子进行适当的变形是解本题的关键.
19.【答案】解:原式=4−3÷3+12
=4−1+12
=312.
【解析】先进行乘方,开方,除法运算,再进行加减运算即可.
本题考查的是二次根式的混合运算,熟知二次根式混合运算的法则是解题的关键.
20.【答案】解:原式=m+5(m+3)(m−3)⋅m+3m+5=1m−3;
当m=5时,原式=15−3=12.
【解析】先根据分式的除法法则,进行化简,再代值计算即可.
本题考查分式的化简求值,熟练掌握分式的性质是关键.
21.【答案】解:(1)如图,OC即为所求;
(2)①∵∠AOB=30∘,OC平分∠AOB,
∴∠BOC=∠AOC=12∠AOB=15∘;
②由(1)知:∠AOC=15∘,
∴∠AOC的补角为180∘−∠AOC=165∘.
【解析】(1)尺规画出角平分线即可;
(2)①根据角平分线平分角即可得出结果;②根据互补的两角和为180度,进行求解即可.
本题考查余角和补角,角平分线的定义,关键是尺规作角平分线,与角平分线有关的计算.
22.【答案】解:(1)22⊕23
=22×3+22+3
=26+25
=64+32
=96;
(2)当2p=3,2q=5,3q=6时.
2p⊕2q
=2pq+2p+q
=(2p)q+2p×2q
=3q+3×5
=6+15
=21.
【解析】(1)根据新定义的运算,把相应的值代入运算即可;
(2)根据新定义的运算、幂的乘方的法则进行运算即可.
本题考查了幂的乘方、新定义的运算;熟练掌握运算法则是解题的关键.
23.【答案】(−2x2+60x)平方米
【解析】解:(1)由图可知:走道的全面积为:2×15x+30x−2x2=−2x2+60x(平方米),
故答案为:(−2x2+60x)平方米;
(2)当x=0.5时:−2x2+60x=−2×0.52+60×0.5=29.5,
故该走道的总面积为:29.5平方米;
(3)25×29.5=737.5(元).
(1)根据图形,列出代数式即可;
(2)将x=0.5代入(1)中的结果进行求解即可;
(3)用单价乘以总面积进行求解即可.
本题考查列代数式,代数式求值,熟练掌握列代数式是关键.
24.【答案】C(x+2)4
【解析】解:(1)y2+8y+16=(y+4)2,利用了完全平方公式法因式分解;
故选:C;
(2)(x2+4x+4)2
=[(x+2)2]2
=(x+2)4;
(3)设x2−6x=y,则:
原式=(y+8)(y+10)+1
=y2+18y+80+1
=y2+18y+81
=(y+9)2
=(x2−6x+9)2
=[(x−3)2]2
=(x−3)4.
(1)利用完全平方公式法因式分解;
(2)利用完全平方公式法因式分解即可;
(3)设x2−6x=y,进行因式分解即可.
本题考查因式分解,掌握换元法因式分解是解题的关键:
25.【答案】解:(1)设每个蛋黄粽的进价为x元,则每个肉粽的进价为(x+0.5)元,
依题意得:600x+0.5=75%×600x,
解得:x=1.5,
经检验,x=1.5是原方程的解,且符合题意,
∴x+0.5=1.5+0.5=2,
答:每个肉粽的进价为2元,每个蛋黄粽的进价为1.5元.
(2)解:购进蛋黄粽的数量为600÷1.5=400(个),
购进肉粽的数量为600÷2=300(个).
依题意得:5×a%×300×(1−40%)+4×2a%×400×(1−50%)=195,
解得:a=7.8.
答:a的值为7.8.
【解析】(1)设每个蛋黄粽的进价为x元,则每个肉粽的进价为(x+0.5)元,利用数量=总价÷单价,结合用600元所购肉粽数量是用600元所购蛋黄粽数量的75%,即可得出关于x的分式方程,解之经检验后可得出每个蛋黄粽的进价,再将其代入(x+0.5)中即可求出每个肉粽的进价;
(2)利用数量=总价÷单价,可求出购进肉粽和蛋黄粽的数量,利用少赚的总利润=每个少赚的利润×销售数量,即可得出关于a的一元一次方程,解之即可求出a的值.
本题考查了一元一次方程的应用以及分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.
26.【答案】解:任务(1):设小长方形长可以站x人,宽可以站y人,根据题意:
x+2y=442x+y=52
解得x=20y=12
则xy=240,3xy=720人
答:本次研学初一年级共有720人参加.
任务(2):设A型号有a辆车,B型号有(20−a)辆,
根据题意得30a+45(20−a)≥720320a+400(20−a)≤7200
解得:10≤a≤12,
∵a为整数
∴a=10,11,12,学校选择3种租车方案
10×320+10×400=7200
11×320+9×400=7120
12×320+8×400=7040,
∴最小租车费用为7040元.
【解析】任务(1):设小长方形长可以站x人,宽可以站y人,根据图中的摆放列出方程求解即可得出答案;
任务(2):设型号有a辆车,型号有(20−a)辆,根据人数大于等于720,费用不超过7200元列出不等式组求解,再根据a范围确定方案即可得出答案.
本题考查了二元一次方程组的应用及一元一次不等式组的应用,读懂题意找到关系式是解题的关键.材料一:将全年级的同学分成了三个人数相同,排列方式也完全相同的队伍进行训练,当三支队伍正好按如图所示的方式站立时,(图中阴影部分即为三支队伍),发现从正前方看有52人,从侧面看有44人.
材料二:基地计划一共租A、B两种型号的客车20辆,根据上表提供的信息要求在保证将全部师生送达目的地的前提下租车费用不超过7200元.
2023-2024学年广西柳州市七年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年广西柳州市七年级(上)期末数学试卷(含详细答案解析),共13页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023-2024学年广西来宾市七年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年广西来宾市七年级(上)期末数学试卷(含详细答案解析),共15页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023-2024学年广西贵港市覃塘区七年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年广西贵港市覃塘区七年级(上)期末数学试卷(含详细答案解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












