高中数学人教A版 (2019)必修 第一册4.2.2 指数函数的图象和性质教学课件ppt

这是一份高中数学人教A版 (2019)必修 第一册4.2.2 指数函数的图象和性质教学课件ppt，共22页。PPT课件主要包含了情境导学，初探新知，思路点拨，备选题，思想点拨等内容，欢迎下载使用。

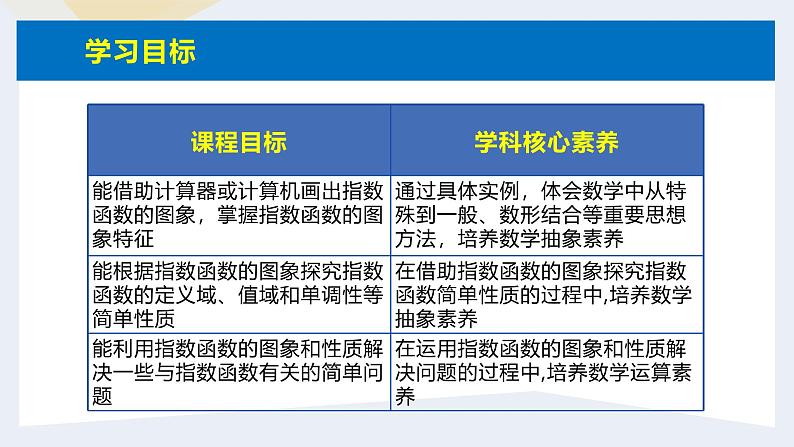
1. 通过具体实例,作出指数函数的图象,由特殊到一般,掌握指数函数的图象特征.2. 结合指数函数的定义和图象,探索指数函数的简单性质,体会数形结合思想的应用.3. 能正确作出指数函数图象并应用指数函数图象和性质解决与指数函数有关的问题.
某位股民购进某支股票，在接下来的交易时间内，他的这只股票先经历了n次涨停(每次上涨10%)，又经历了n次跌停(每次下跌10%)，试探究该股民这只股票的盈亏情况(不考虑其他费用).思考可以通过什么方式直观地展示出该股票的情况．
【活动1】作出指数函数的图象并探索其变化规律
【问题2 】你能将上述指数函数的图象一般化吗？
【问题3】我们已经研究了指数函数的图象，那么接下来要研究指数函数的哪些知识呢？
【活动2】结合指数函数的图象，探究指数函数的性质
【问题4】我们一般研究函数的哪些性质？如何研究？
【问题6】你能总结出指数函数的性质吗？
【问题5】作出指数函数y=2x与y= x的图象,函数y=10x与y= x的图象,如图2,你有什么发现?你能推广到更一般的情形吗?
典例精析
【例1】函数f(x)＝ax－b的图象如图所示，其中a，b为常数，则下列结论中正确的是(　　)A. a>1，b<0B. a>1，b>0C. 00D. 0思路点拨：利用指数函数的图象与性质判断。
【解】由f(x)＝ax－b的图象可以观察出，函数f(x)＝ax－b在定义域上单调递减，所以0【方法规律】(1) 已知函数解析式判断其图象一般是取特殊点，判断选项中的图象是否过这些点，若不满足则排除．(2) 对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换而得到．特别地，当底数a与1的大小关系不确定时应注意分类讨论．
【变式训练1】已知函数f(x)＝(x－a)(x－b)(其中a>b)，若f(x)的图象如图所示，则函数g(x)＝ax＋b的图象大致为(　　)
思路点拨：求与指数函数有关的函数的定义域时，只需使函数式有意义即可，求值域时可以从相应函数的定义域入手或依据单调性求解．
【例2】求下列函数的定义域和值域：
【方法规律】求与指数函数有关的函数的定义域时，只需使函数有意义即可；求值域时，可结合指数函数的图象，依据函数的单调性，在定义域的范围内求值域.
【方法规律】(1) 在含有绝对值的函数图象绘制中,注意函数的对称性在作图中的作用,同时把握好指数函数本身的图象特点,如定义域、值域、定点,以确定作图范围;(2) 巧用图象变换:函数图象的平移变换(左右平移、上下平移)、对称变换、翻折变换在本题中得到充分的运用.注意在运用中总结函数的性质及其变化规律.
通过本节课的学习，你学到了哪些知识？
2.你认为本节课的重点和难点是什么？