必修 第一册4.3.2 对数的运算示范课课件ppt

这是一份必修 第一册4.3.2 对数的运算示范课课件ppt，共24页。PPT课件主要包含了情境导学，初探新知，变式训练3等内容，欢迎下载使用。
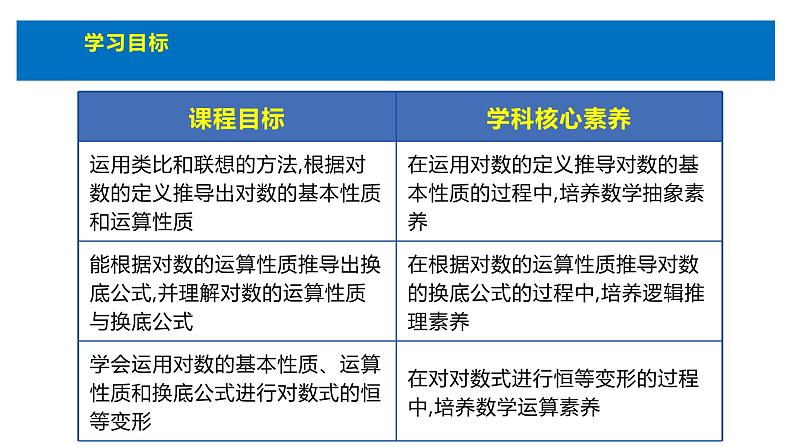
1. 通过类比和联想,将指数相关的性质和运算性质转化为对数的性质和运算性质.2. 能根据对数运算性质推导出换底公式,并理解对数的运算性质与换底公式.3. 学会运用对数的性质、运算性质和换底公式进行对数式求值、化简等恒等变形.
某工厂生产一种溶液，按市场要求杂质含量不得超过0.1%，而这种溶液最初的杂质含量为2%.现进行过滤，已知每过滤一次杂质含量减少1/3，为使产品达到市场要求，则至少得过滤多少次？(参考数据:lg 2≈0.301，lg 3≈0.477)
【活动1】　探究对数运算性质
【问题1】我们学过的对数的性质有哪些？
【问题2】我们知道了对数和指数间的关系，你打算怎么研究对数运算性质？
【问题3】计算lg24,lg216,lg264的值，你有什么发现？
【问题4】对于lgaM,lgaN,lga(MN),你有何猜想？
【问题5】上述猜想是否具有一般性？如何证明？
【问题7】上述猜想是否具有一般性?请试着推导.
【活动2】　探究对数换底公式
【问题8】如何计算lg25?(参考数据：lg5=0.699,lg2=0.301,ln5=1.609,ln2=0.693)
【问题9】lgab(a>0,且a≠1，b>0)能否转化为以c(c>0,且c≠1)为底的对数？
【问题10】上述结论如何证明？
典例精析
思路点拨：先要认真审题，根据目标式子的特点，利用幂的运算将幂的底数变得简单，然后再利用对数运算性质求解．解题时，注意对数的性质、运算法则的合理运用．
【方法规律】对数运算的解题技巧：(1) 拆分：先利用幂的运算把底数或真数变形，化成分数指数幂的形式，使幂的底数变得简单，再利用对数的运算性质化简合并．(2) 合并：将对数式化为同底数对数的和、差或倍数运算，然后逆用对数的运算性质，转化为同底对数真数的积、商、幂的运算．
思路点拨：(1) 认真审题，注意对数的性质、运算法则及换底公式的合理运用．(2) 利用对数与指数的互化，表示出a，b，根据对数的性质和运算性质及换底公式求解．
【方法规律】当底数不同时，考虑使用换底公式将不同底的对数化成同底，然后使用同底对数的运算性质解决问题．在数学运算中，常将底数转换为以e为底的自然对数或以10为底的常用对数，方便计算．
思路点拨：利用换底公式进行求值时要做到“化异为同”,在恒等变形和求值化简中,都需要对具体条件选择适当的底数,同时注意换底公式与对数运算性质的相结合.
【方法规律】(1) 统一化:所求为对数式,条件转为对数式.(2) 选底数:针对具体问题,选择恰当的底数.(3) 会结合:学会换底公式与对数运算法则结合使用.
通过本节课的学习，你学到了哪些知识？
2.你认为本节课的重点和难点是什么？
4. 若集合{x，xy，lg (xy)}＝{0，|x|，y}，则lg8(x2＋y2)6的值为________.