圆 复习课课件

这是一份圆 复习课课件，共33页。

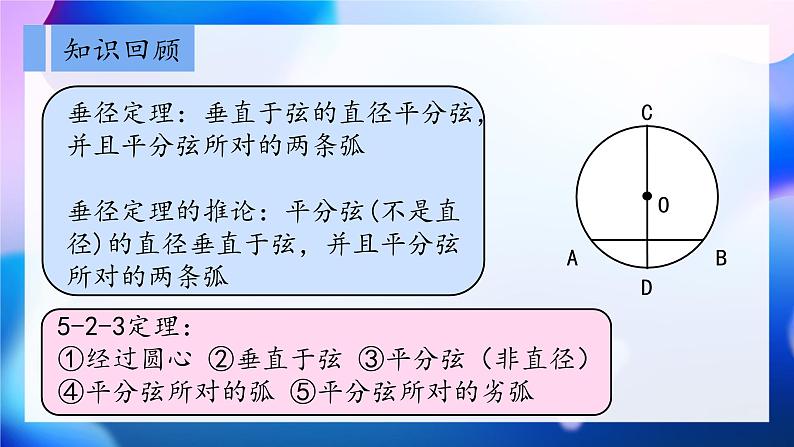
素养提升1.在学习圆的过程中，学生需要能够想象和描述圆的基本形状和特征，理解圆心、半径、直径等基本概念，并能够运用这些概念进行判断和计算.2.通过培养空间观念，学生能够在头脑中形成对圆的形象认知，进一步加深对圆的理解和运用.3.学生需要能够运用逻辑思维和推理能力来探究圆的性质和规律.圆的相关概念OA描述性定义：如右图所示，圆可以看成在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形.其圆心固定的端点O叫做圆心，线段OA叫做半径集合性定义：圆可以看成是平面上所有到定点的距离等于定长的点的集合以点O为圆心的圆，记作 O，读作“圆O”BC圆的相关概念弦：连接圆上任意两点的线段，如右图中“弦AC”直径：经过圆心的弦，如右图“直径AB”弧：圆上任意两点间的部分，简称弧优弧：大于半圆的弧，用三个字母表示劣弧：小于半圆的弧，用两个字母表示等圆：能够重合的两个圆等弧：在同圆或等圆中，能够互相重合的弧下列说法错误的是（ ）A.直径是圆中最长的弦B.长度相等的两条弧是等弧C.面积相等的两个圆是等圆D.半径相等的两个半圆是等弧小题精练B知识回顾垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧垂径定理的推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧5-2-3定理：①经过圆心 ②垂直于弦 ③平分弦（非直径）④平分弦所对的弧 ⑤平分弦所对的劣弧课堂小练在圆O中，半径OC与弦AB垂直于点D，且AB=8，OC=5，则CD的长是（ ）CA.3 B.2.5 C.2 D.1圆心角圆心角：顶点在圆心的角叫做圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等重要推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的优弧和劣弧分别相等课上习题在圆O中，点C是弧AB的中点，∠OAB=40°，则∠BOC等于（ ）BA.40° B.50° C.70° D.80°圆周角顶点在圆上，并且两边都与圆相交A定理：一条弧所对的圆周角等于它所对的圆心角的一半重要推论①同弧或等弧所对的圆周角相等②半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径小题精练点A,B,C,D在圆O上，C是弧AB的中点，∠CDB=25°，则∠AOB的度数是（ ）BA.50° B.100° C.125° D.150°内接四边形圆内接多边形：如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆 圆内接四边形的对角互补 圆内接四边形的一个外角等于它的 内对角(拓展)性质跟踪训练四边形ABCD内接于圆O，E为BC延长线上一点，若∠A=n°，则∠DCE= 点与圆点在圆外点在圆上点在圆内点到圆心得距离大于半径点到圆心得距离等于半径点到圆心得距离小于半径d＞rd=rd＜r直线与圆 相交 相切 相离2个公共点d=rd＞r1个公共点0个公共点d＜r课堂小练在Rt△ABC中，∠BCA=90°，AC=3cm，BC=4cm，以点C为圆心画圆，当半径r为下列值时，圆C与直线AB有怎样的位置关系？为什么？（1）r=2cm （2）r=2.4cm （3）r=3cm圆与圆外离内含外切内切相交公共点个数00121数量关系0≤d＜r2-r1d＞r1+r2d=r1+r2d=r2-r1r2-r1＜d＜r2+r1r2＞r1确定圆的条件过几点可以做圆？过不在同一条直线上的三点切 线切线的性质定理：圆的切线垂直于过切点的半径课堂小练圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是（ ）BA.25°B.40°C.50°D.65°切线长切线长的定义：经过圆外一点作圆的切线，这点和切点之间线段的长，叫做这点到圆的切线长切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角课堂小练从圆外一点引圆O的两条切线PA,PB,切点分别为A,B，如果∠APB=60°，PA=8，那么弦AB的长是（ ）BA.4B.8C.D.外心内心圆O是△ABC的内切圆，切点分别为D,E,F，若∠DEF=54°，求∠BAC的度数.小题精练正多边形中心：正多边形外接圆的圆心半径：正多边形外接圆的半径中心角：正多边形每一边所对的圆心角边心距：正多边形的中心到正多边形的一边的距离正n边形每个内角为：正n边形每个外角为：弧 长ABOCn°在半径为R的圆中，n°的圆心角所对的弧长的计算公式为课堂小练ABDOC圆O的半径为3，四边形ABCD内接于圆O，连接OB，OD.若∠BOD=∠BCD，则劣弧BD的长为（ ）CA.πB.1.5πC.2πD.3π扇 形扇形的概念：由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形面积：周长：课堂小练从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形，则此扇形的面积为（ ）m2AA.0.5πB.1.5πC.πD.2π圆 锥小刚用一张半径为24cm的扇形纸板做一个圆锥形小丑帽子的侧面(接缝忽略不计)，如果做成的圆锥形小丑帽子的底面半径为10cm，那么这张扇形纸板的面积是( )A.120πcm2B.240πcm2C.260πcm2D.480πcm2B小题精练反证法小题精练求证：在一个三角形中，至少有一个内角小于或等于60度证明：假设在一个三角形中没有一个角小于或等于60°，即都大于60°，那么这个三角形的三个内角之和就会大于180°.这与定理“三角形的三个内角之和等于180°”相矛盾，原命题正确.